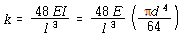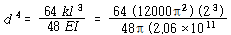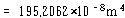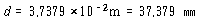System Dynamics
8.1 진동의 기초 (Fundamentals of Vibration)
8.1.1 진동의 기본 개념 (Basin Concepts of Vibtation)
8.1.2 스프링 요소 (Spring Elements)
8.1.3 질량 혹은 관성 요소 (Mass or Inertia Elements)
8.1.4 감쇠 요소 (Damping Elements)
8.2 1 자유도계의 자유진동 (Free Vibration of Single Degree of Freedom Systems)
8.2.1 비감쇠 병진계의 자유진동 (Free Vibration of an Undamped Translational System)
8.2.2 비감쇠 비틀림 시스템의 자유진동 (Free Vibration of Undamped Torsional System)
8.2.3 점성 감쇠율의 자유진동 (Free Vibration with Viscous Damping)
8.3 1 자유도계의 강제진동 (Forced Vibration of Single Degree of Freedon Systems)
8.3.2 운동방정식 (Equation of Motion)
8.3.3 조화가진에 대한 감쇠 시스템의 응답 (Response of a Damped System under Harmonic Force)
8.3.4 회전 불평형에 대한 감쇠 시스템의 응답 (Response of Damped System under Rotating Unbalance)
8.1 진동의 기초 (Fundamentals of Vibration)
8.1.1 진동의 기본 개념 (Basic Concepts of Vibration)
8.1.1.1 振動 (Vibration)
시간의 간격을 두고 반복해서 나타나는 운동은 무엇이든 진동(Vibration) 혹은 Oscillation이라 한다. 진자의 흔들림 혹은 퉁겨진 기타줄의 운동은 전형적인 진동을 보여주는 것이다. 진동의 이론은 흔들리는 물체의 운동과 그 물체와 관련된 힘을 연구하는 것이다.
8.1.1.2 振動 시스템의 基本要素 (Elementary Parts of Vibrating Systems)
일반적으로 진동시스템은 위치에너지(스프링 혹은 탄성)를 저장하기 위한 장치, 운동에너지(질량 및 관성)를 저장하기 위한 장치, 그리고 점차적으로 에너지가 감소되는 장치(댐퍼)로 구성되어 있다.
시스템의 진동은 교대로 위치에너지를 운동에너지로, 운동에너지를 위치에너지로 전환하는 것을 필요로 하고 있다. 만약, 시스템이 감쇠된다면 약간의 에너지가 진동의 매 사이클마다 소멸되고, 정상상태의 진동을 유지하려면 외부 에너지로부터 이 소멸 부분을 대치해야만 한다.
일예로서 그림 8-1의 간단한 단진자의 진동을 고려해보자. 질량 m의 추를 각변위 θ만큼 움직인 후 놓아보자. 1의 위치에서는 추의 속도, 즉 운동에너지는 영이다. 그러나, 이 추는 기준위치 2에 대해 ![]() 의 위치에너지를 갖는다. 중력 mg 가 점 0에 대하여
의 위치에너지를 갖는다. 중력 mg 가 점 0에 대하여 ![]() 의 토오크를 유발하기 때문에, 추는 위치 1로부터 왼쪽으로 흔들리기 시작한다. 이 흔들림은 시계방향으로 어떤 각가속도를 추에 주게되고 위치 2에 도달할 때까지는 모든 위치에너지가 운동에너지로 전환된다. 이로 인하여 추는 위치 2에서 멈추지 않고 위치 3으로 계속 이동한다. 그러나 추가 위치 2를 통과함에 따라 반시계방향의 토오크(중력으로 인한)가 추에 가해지기 시작하고 감가속을 야기한다. 마지막에는 추의 속도가 왼쪽의 끝점에서 영이 된다. 지금까지 추의 모든 운동에너지는 위치에너지로 전환된다. 다시 중력 토오크가 작용하기 시작하고 추에 반시계방향의 속도를 주게된다. 이로 인해 추는 점진적으로 증가하는 속도로 반대방향으로 이동하기 시작한다. 이와 같은 순서의 운동이 계속 반복되고 진자는 계속 진동을 하게된다.
의 토오크를 유발하기 때문에, 추는 위치 1로부터 왼쪽으로 흔들리기 시작한다. 이 흔들림은 시계방향으로 어떤 각가속도를 추에 주게되고 위치 2에 도달할 때까지는 모든 위치에너지가 운동에너지로 전환된다. 이로 인하여 추는 위치 2에서 멈추지 않고 위치 3으로 계속 이동한다. 그러나 추가 위치 2를 통과함에 따라 반시계방향의 토오크(중력으로 인한)가 추에 가해지기 시작하고 감가속을 야기한다. 마지막에는 추의 속도가 왼쪽의 끝점에서 영이 된다. 지금까지 추의 모든 운동에너지는 위치에너지로 전환된다. 다시 중력 토오크가 작용하기 시작하고 추에 반시계방향의 속도를 주게된다. 이로 인해 추는 점진적으로 증가하는 속도로 반대방향으로 이동하기 시작한다. 이와 같은 순서의 운동이 계속 반복되고 진자는 계속 진동을 하게된다.
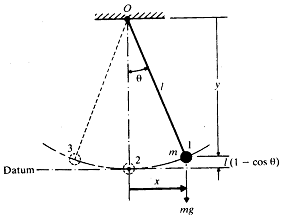
그림 8-1 단진자
그러나, 진동의 크기(θ)는 점차적으로 감소하고 진자는 주위의 매체(공기)가 제공한 저항(감쇠)으로 인하여 결국 정지한다. 이는 공기의 감쇠로 인하여 진동의 매 사이클마다 약간의 에너지가 감소됨을 의미한다.
8.1.1.3 自由度 (Degree of Freedom)
어떤 순간 시스템의 모든 부분의 위치를 완벽하게 결정하기 위해 요구되어지는 독립좌표의 최소수를 시스템의 자유도라 정의한다. 그림 8-1에 나타난 단진자뿐만 아니라 그림 8-2의 각각의 시스템도 1 자유도계를 나타낸다.
예로서 단진자의 운동 (그림 8-1)은 각θ의 항으로 혹은 직교좌표 χ, y 의 항으로 나타낼 수 있다. 만약 χ, y 의 좌표가 운동을 묘사하기 위해 사용된다면, 이 좌표들은 독립좌표가 아님을 인식해야만 한다. 그들은 ![]() (ℓ:진자의 일정길이)로 서로 연관되어 있다. 그러므로, 어떤 하나의 좌표로 진자의 운동을 묘사할 수 있다. 이 예제에서 독립좌표로서 θ의 선택이 χ 혹은 y 의 선택보다는 더 편리한 것이다. 2 및 3 자유도의 예가 그림 8-3 및 그림 8-4에 각각 나타나있다. 그림 8-3(a)는 2개의 선형좌표
(ℓ:진자의 일정길이)로 서로 연관되어 있다. 그러므로, 어떤 하나의 좌표로 진자의 운동을 묘사할 수 있다. 이 예제에서 독립좌표로서 θ의 선택이 χ 혹은 y 의 선택보다는 더 편리한 것이다. 2 및 3 자유도의 예가 그림 8-3 및 그림 8-4에 각각 나타나있다. 그림 8-3(a)는 2개의 선형좌표 ![]() 과
과 ![]() 로 묘사되는 2 질량 – 2 스프링 시스템을 보여준다.
로 묘사되는 2 질량 – 2 스프링 시스템을 보여준다.
시스템의 운동을 묘사하기 위해 필요한 좌표는 일련의 일반화 좌표를 구성한다. 일반화 좌표는 보통 ![]() ,
, ![]() 로 표시되고 직교좌표 혹은 비직교좌표로 표시된다.
로 표시되고 직교좌표 혹은 비직교좌표로 표시된다.
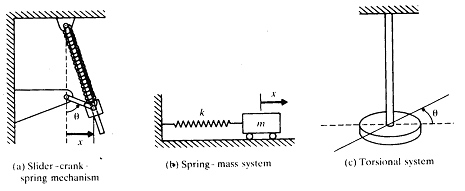
그림 8-2 1 자유도계
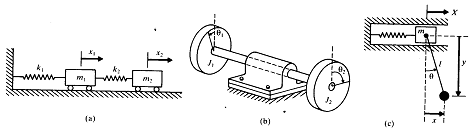
그림 8-3 2 자유도계
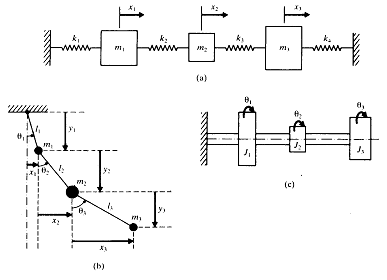
그림 8-4 3 자유도계
8.1.1.4 不連續 및 連續系 (Discrete and Continuous Systems)
실제 시스템은 그림 8-1~8-4에서 보여준 단순시스템에서와 같이 유한 수의 자유도로 묘사될 수 있다. 변형 가능한 부재를 포함하고 있는 시스템들과 같은 여러 다른 시스템들은 무한수의 자유도를 가지고 있다. 간단한 예로서 그림 8-5의 내다지 보를 생각해보자. 보는 무한개의 질점을 가지고 있기 때문에 보의 처짐을 묘사하기 위해서는 무한 수의 좌표를 필요로 한다. 무한 수의 좌표는 보의 처짐선을 주게된다. 그러므로, 내다지보는 무한수의 자유도를 갖게된다. 대부분의 구조물 및 기계 시스템은 변형 가능한 부재를 갖고 있고 무한수의 자유도를 갖는다.
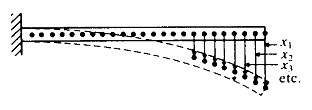
그림 8-5 내다지보
유한수의 자유도를 갖는 시스템을 불연속 혹은 Lumped Parameter 시스템이라 부르고 무한수의 자유도를 갖는 시스템을 연속 혹은 Distributed 시스템이라고 부른다.
8.1.2 스프링 요소 (Spring Elements)
선형의 스프링은 일반적으로 무시할만한 질량과 감쇠를 갖고있는 것으로 추정되는 일종의 기계적인 링크이다. 스프링의 양단 사이에 상대적인 운동이 있으면 스프링에는 힘이 발생된다. 스프링력은 변형량에 비례하고
F =![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (1)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (1)
로 주어진다.
여기서 F는 스프링력, χ는 변형 (한쪽 끝을 기준하여 다른 한쪽 끝의 변위), 그리고, ![]() 는 스프링 강성 혹은 스프링 상수라고 하는 비례상수이다. 만약
는 스프링 강성 혹은 스프링 상수라고 하는 비례상수이다. 만약 ![]() 에 대한 F를 그래프로 나타내면 식 (1)에 따라 직선이 된다. 스프링의 변형을 위해 가해진 일은 스프링에서 변형 혹은 위치에너지로 축적된다. 실제 스프링은 비선형이고 식 (1)은 변형의 어떤 범위 내에서만 유효하다. 변형이 어떤 값을 초과하면 (그림 8-6의 A점 이후), 응력은 후크 법칙의 비례한도를 초과하고 변형은 더 이상 가해진 힘에 비례하지 않는다. 대부분의 실제 적용에 있어서는 변형이 적다고 가정하고 식 (1)의 선형관계를 사용한다. 스프링의 힘-변형 관계가 비선형이더라도 때때로 선형화라고 알려진 과정을 사용하여 선형으로 개략화한다.
에 대한 F를 그래프로 나타내면 식 (1)에 따라 직선이 된다. 스프링의 변형을 위해 가해진 일은 스프링에서 변형 혹은 위치에너지로 축적된다. 실제 스프링은 비선형이고 식 (1)은 변형의 어떤 범위 내에서만 유효하다. 변형이 어떤 값을 초과하면 (그림 8-6의 A점 이후), 응력은 후크 법칙의 비례한도를 초과하고 변형은 더 이상 가해진 힘에 비례하지 않는다. 대부분의 실제 적용에 있어서는 변형이 적다고 가정하고 식 (1)의 선형관계를 사용한다. 스프링의 힘-변형 관계가 비선형이더라도 때때로 선형화라고 알려진 과정을 사용하여 선형으로 개략화한다.
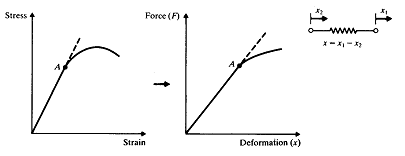
그림 8-6 비례한도를 초과한 비선형
그림 8-7과 같은 비선형의 힘-변형 관계를 갖는 스프링을 생각해보자. 먼저 힘 Fo를 가하면 ![]() 만큼 변형한다. 이 위치에서 평형상태를 유지하고 스프링 반력은 -Fo와 같다. 이 상태에서 힘 ΔF를 더 가하면 Δχ 만큼 더 변형하고
만큼 변형한다. 이 위치에서 평형상태를 유지하고 스프링 반력은 -Fo와 같다. 이 상태에서 힘 ΔF를 더 가하면 Δχ 만큼 더 변형하고 ![]() 가 된다.
가 된다.
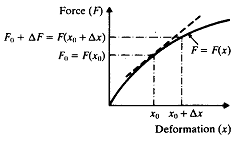
그림 8-7 선형화 과정
함수 F는 ![]() 에 대한 Taylor의 급수 전개를 이용하여 전개할 수 있다.
에 대한 Taylor의 급수 전개를 이용하여 전개할 수 있다.
![]() – – – – – – – – – (2)
– – – – – – – – – (2)
Δχ는 작기 때문에 높은 계수의 항목은 무시할 수 있고 식 (2)는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (3)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (3)
![]() 이기 때문에
이기 때문에
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (4)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (4)
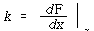
식 (4)는 바람직한 선형관계이고 스프링상수 k 는 F = F(χ)의 미분으로 구해지며 평형위치 ![]() 에서 평가된 것이다. 식 (4)는 단순화의 목적으로 사용할 수 있으나 때때로 개략화의 가정 중에 포함된 오차가 상당히 커질 수 있다.
에서 평가된 것이다. 식 (4)는 단순화의 목적으로 사용할 수 있으나 때때로 개략화의 가정 중에 포함된 오차가 상당히 커질 수 있다.
스프링상수(강성계수)란 부품이나 구조물을 어떤 거리만큼 휘거나 변형시키는데 필요한 힘이라고 간단히 정의할 수 있다. 강성의 단위는 통상 N/m으로 나타낸다. 예를 들면 코일 스프링 위에 100 N의 무게를 올려놓았을 때 0.01 m의 처짐을 가져오면 스프링 강성 즉, “![]() ” 계수는 10000 N/m이다. 또한 시스템에 대한 강성 즉, “
” 계수는 10000 N/m이다. 또한 시스템에 대한 강성 즉, “![]() ” 계수를 알면 실제의 강성력은 그 결과로 생기는 변위에 직접 비례한다. 따라서 강성은 시스템의 비례함수인 변위와 연관되며 진동주파수와는 별개임을 알 수 있다.
” 계수를 알면 실제의 강성력은 그 결과로 생기는 변위에 직접 비례한다. 따라서 강성은 시스템의 비례함수인 변위와 연관되며 진동주파수와는 별개임을 알 수 있다.
보와 같은 탄성요소도 스프링과 같이 거동한다. 예를 들면 그림 8-8과 같이 끝에 질량 m 이 있는 내다지보를 생각해보자. 간단하게 질량 m 에 비해 보의 질량은 무시할 만 하다고 가정한다. 이 보의 자유단에서의 정적처짐이
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (5)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (5)
W = mg 에서 W는 질량 m 의 무게, E는 Young 계수, I는 단면관성 모멘트이다. 즉, 스프링상수는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – -(6)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – -(6)
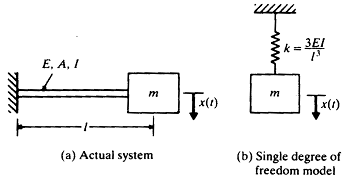
그림 8-8 내다지보
8.1.2.1 스프링의 組合 (Combination of Springs)
실제 적용에 있어서는 다수의 선형 스프링이 복합되어 사용된다. 이러한 스프링들은 다음에서 나타난 바와 같이 하나의 상당 스프링으로 조합할 수 있다.
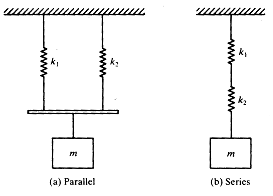
그림 8-9 스프링의 조합
경우(1) : 병렬 스프링
그림 8-9(a)와 같이 스프링이 병렬로 되어 있으면
![]() (7)
(7)
![]() 는 질량 m 의 정적처짐이다. 만약,
는 질량 m 의 정적처짐이다. 만약, ![]() 를 두 스프링의 조합에 의한 상당 스프링상수라면 같은 정적처짐
를 두 스프링의 조합에 의한 상당 스프링상수라면 같은 정적처짐![]() 에 대해
에 대해
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (8)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (8)
식 (7)과 식 (8)로부터
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (9)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (9)
일반적으로 스프링상수 ![]() ,
, ![]() , …
, … ![]() 을 병렬로 구성된
을 병렬로 구성된 ![]() 개의 스프링에 대해서는 상당스프링 상수가
개의 스프링에 대해서는 상당스프링 상수가
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (10)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (10)
경우(2) : 직렬 스프링
다음은 그림 8-9(b)와 같이 직렬로 연결된 2개의 스프링을 생각한다.
2개의 스프링은 같은 힘 W에 종속되어 있기 때문에 평형상태에 대해
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (11)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (11)
![]() 및
및 ![]() 는 스프링 1과 2의 변형량이다. 총 변형량은 정적처짐
는 스프링 1과 2의 변형량이다. 총 변형량은 정적처짐![]() 와 동일하다.
와 동일하다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (12)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (12)
만약 ![]() 가 상당 스프링 상수를 나타낸다면 같은 정적처짐에 대해
가 상당 스프링 상수를 나타낸다면 같은 정적처짐에 대해
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (13)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (13)
식 (11)과 식 (13)으로부터
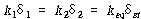
혹은
![]() ,
, ![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (14)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (14)
![]() 및
및 ![]() 를 식 (12)에 대입하면
를 식 (12)에 대입하면
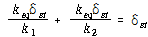
즉
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (15)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (15)
식 (15)를 일반화하면
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (16)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (16)
[예제] 그림 8-10(a)와 같이 무게 W가 천장 크레인에 의해 인양된다. Girder는 길이 ![]() , 굽힘 강성계수 EI를 갖는 균일보이고 두 케이블의 각각의 길이는
, 굽힘 강성계수 EI를 갖는 균일보이고 두 케이블의 각각의 길이는![]() , 직경 d 및 영계수 E이다. 트롤리, 전동기, 케이블 및 후크의 질량은 무시할 만 하다고 가정하고, Girder와 케이블의 상당 스프링 상수를 구하라.
, 직경 d 및 영계수 E이다. 트롤리, 전동기, 케이블 및 후크의 질량은 무시할 만 하다고 가정하고, Girder와 케이블의 상당 스프링 상수를 구하라.
[해] Girder를 단순히 어떤 부하를 지지하는 보로 생각하면 그 스프링 상수는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (17)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (17)
케이블은 길이 방향의 부하를 받기 때문에 각 케이블의 강성은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (18)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (18)
두 개의 병렬 케이블의 총강성은 ![]() 이다. 결국, Girder와 케이블은 직렬 스프링으로 간주할 수 있고 상당 스프링상수
이다. 결국, Girder와 케이블은 직렬 스프링으로 간주할 수 있고 상당 스프링상수 ![]() 는
는
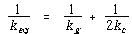
혹은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (19)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – (19)
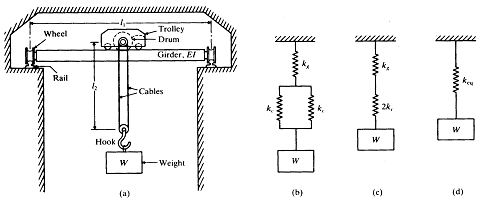
그림 8-10 천정 크레인
8.1.3 질량 혹은 관성요소 (Mass or Inertia Elements)
질량 혹은 관성요소는 강체라고 가정한다. 즉, 강체의 속도가 변할 때는 언제나 운동에너지를 잃거나 얻는다. 뉴튼의 운동 제2법칙으로부터 질량과 그 가속도의 곱은 그 질량에 가해진 힘과 같다. 일은 힘의 방향으로의 변위에 힘을 곱한 것과 같고 질량에 가해진 일은 질량의 운동에너지 형태로 축적된다.
대부분의 경우, 실제 진동시스템을 표현하기 위해서는 수학적 모델을 사용해야만 한다.
8.1.3.1 質量의 組合 (Combination of Masses)
실제 적용에 있어서는 다수의 질량이 조합되어 나타난다. 분석을 간단히 하기 위해 이 질량들을 하나의 상당 질량으로 나타낸다.
경우(1) : 레버에 의한 연결된 병진운동 질량
그림 8-11에서 보는 바와 같이 한쪽 끝이 피봇팅되어 있는 레버에 놓여있는 질량을 생각해 보자. 상당질량이 레버의 어떤 위치에 있을 수 있다고 가정한다. 세부적으로 나타내기 위해서 상당 질량이 ![]() 의 위치에 있다고 가정한다. 질량
의 위치에 있다고 가정한다. 질량 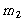 의 속도(
의 속도(![]() )는 다음과 같이 레버에 대해 작은 각변위를 가정함으로써
)는 다음과 같이 레버에 대해 작은 각변위를 가정함으로써 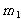 의 속도(
의 속도(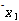 ) 항으로 표현할 수 있다.
) 항으로 표현할 수 있다.
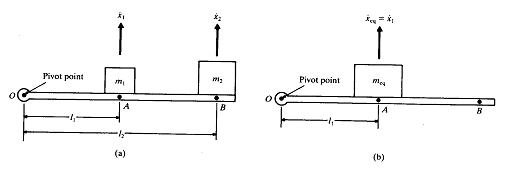
그림 8-11 레버에 연결된 병진운동 질량
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (20)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (20)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (21)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (21)
두 질량시스템의 운동에너지가 상당 질량시스템의 운동에너지와 같다고 하면
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (22)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – (22)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (23)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (23)
경우(2) : 병진 및 회전운동 질량의 합성
병진속도 ![]() 인 질량 m 이 회전속도
인 질량 m 이 회전속도![]() 인 질량(관성 질량모멘트
인 질량(관성 질량모멘트 ![]() )에 합성된 경우 (그림 8-12)를 생각해보자. 이 두 질량은 하나의 병진운동 상당질량
)에 합성된 경우 (그림 8-12)를 생각해보자. 이 두 질량은 하나의 병진운동 상당질량 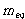 나 상당 회전질량
나 상당 회전질량 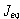 로 나타낼 수 있다.
로 나타낼 수 있다.
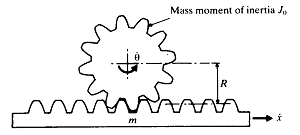
그림 8-12 병진 및 회전질량의 합성
[1] 상당 병진질량 : 두 질량의 운동에너지는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (24)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (24)
상당질량의 운동에너지는 다음과 같이 표현된다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (25)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (25)
![]() ,
, ![]() 이므로 T 및
이므로 T 및![]() 는
는
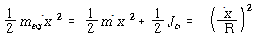
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (26)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (26)
[2] 상당 회전질량 :
![]() ,
, 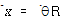 ,
,
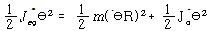
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (27)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (27)
8.1.4 감쇠요소 (Damping Elements)
감쇠는 시스템의 진동 속도를 줄이는 성향이라 할 수 있다. 예를 들면 종과 같은 물체가 타격을 받으면 진동을 일으키는데 그 충격력은 강성 및 질량이 본래부터 가지고 있는 힘을 이겨내지만 궁극적으로는 진동이 소멸된다. 감쇠가 클수록 진동은 보다 빨리 소멸하게 된다. 감쇠기는 질량이나 탄성을 갖지 않는 것으로 가정되며 감쇠력은 단지 감쇠기의 양단사이에 상대속도가 있어야만 존재한다. 감쇠기로 입력되는 에너지 혹은 일은 열이나 소리로 전환된다. 즉 감쇠요소는 비보존적이다. 감쇠는 다음과 같은 형태의 하나이거나 그 이상으로 되어있다.
점성감쇠 : 점성감쇠는 진동 분석시에 가장 일반적으로 사용되는 감쇠 메커니즘이다. 이러한 형태의 감쇠는 실린더의 피스톤 주위 혹은 베어링의 저널 주위로의 슬롯(Slot)을 통해 점성유체가 흐를 때 나타난다. 점성감쇠에 있어서 감쇠력은 진동체의 속도에 비례한다.
쿨롬 혹은 건마찰 감쇠 : 감쇠력은 그 크기가 일정하나 진동체의 운동방향과 반대이다. 이 힘은 두 미끄럼면 사이의 운동마찰에 의해 야기된다.
히스테릭(물질 혹은 고체) 감쇠 : 재료가 변형할 때 재료에 의해 에너지가 흡수되고 소산된다. 이 효과는 변형이 일어남에 따라 미끄러지는 내부면 사이의 마찰에 기인한다.
8.1.4.1 粘性 減衰器의 構成 (Construction of Viscous Dampers)
점성 감쇠기는 거리 d 만큼 분리되고 판사이의 점성계수가 μ인 두 평행판을 사용하여 구성할 수 있다 (그림 8-13).

그림 8-13 점성유체가 있는 평행판
한 판은 고정되고 다른 판이 ![]() 의 속도로 움직인다면 유체에 전단력이 작용한다. 이는 운동과 반대의 수평력 F를 야기한다. 이 저항 즉 감쇠력 F는 상대속도
의 속도로 움직인다면 유체에 전단력이 작용한다. 이는 운동과 반대의 수평력 F를 야기한다. 이 저항 즉 감쇠력 F는 상대속도 ![]() 에 비례하고
에 비례하고
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (28)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (28)
c =μA/ d 는 감쇠상수라고 한다. 비록 그림 8-13의 감쇠기는 넓은 범위의 속도 ![]() 에 대해서 선형이지만 실제적인 감쇠를 발생시키기 위해서는 아주 좁은 간격 d 나 아주 넓은 면적(A)의 판을 필요로 한다. 그래서 비선형의 힘-속도 관계를 갖는 장치를 사용하게 된다 (그림 8-14).
에 대해서 선형이지만 실제적인 감쇠를 발생시키기 위해서는 아주 좁은 간격 d 나 아주 넓은 면적(A)의 판을 필요로 한다. 그래서 비선형의 힘-속도 관계를 갖는 장치를 사용하게 된다 (그림 8-14).
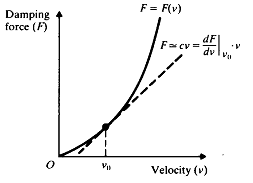
그림 8-14 비선형 감쇠기의 특성
만약 감쇠기가 비선형이라면 비선형 스프링의 경우와 같이 선형화 절차가 일반적으로 필요하게 된다.
8.1.4.2 減衰器의 組合 (Combination of Dampers)
감쇠기가 조합으로 구성될 때 전 절의 방법과 유사한 방법을 채용함으로써 상당감쇠기로 대치할 수 있다.
[예제] 그림 8-15의 대시포트의 감쇠상수를 계산하라.
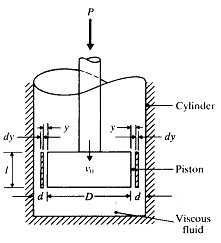
그림 8-15 대시포트
[해] 그림 8-15에서 보는 바와 같이 대시포트는 직경 D, 길이 ℓ의 피스톤이 점성계수 μ인 액체로 채워진 실린더 내에서 ![]() 속도로 움직이고 있다. 피스톤과 실린더 벽사이의 간극을 d 라고 한다. 운동 표면으로부터 y 의 거리의 속도 및 전단응력을
속도로 움직이고 있다. 피스톤과 실린더 벽사이의 간극을 d 라고 한다. 운동 표면으로부터 y 의 거리의 속도 및 전단응력을 ![]() 및 τ라하고
및 τ라하고 ![]() 거리의 속도 및 전단응력을
거리의 속도 및 전단응력을 ![]() 및 τ+dτ 라 한다.
및 τ+dτ 라 한다. ![]() 는 실린더 벽쪽으로 갈수록 속도가 감소한다는 것을 의미한다. 이 환형의 링에서의 점성력은
는 실린더 벽쪽으로 갈수록 속도가 감소한다는 것을 의미한다. 이 환형의 링에서의 점성력은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (29)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (29)
전단응력은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (30)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (30)
-는 감소하는 속도 기울기와 일치한다.
식 (29)에 식 (30)을 대입하면
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (31)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (31)
피스톤에 가해진 힘은 요소의 양끝에 압력차이를 일으키며 다음과 같이 주어진다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (32)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (32)
요소의 끝에서 가해진 압력에 의한 힘은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (33)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (33)
![]() 는
는 ![]() 와
와 ![]() 사이의 환형면적을 나타내고 유체의 운동방향에 있어서 균일한 평균속도를 가정한다면 식 (34)와 식 (33)의 힘은 같아야만 한다. 그러므로
사이의 환형면적을 나타내고 유체의 운동방향에 있어서 균일한 평균속도를 가정한다면 식 (34)와 식 (33)의 힘은 같아야만 한다. 그러므로
![]() , 혹은
, 혹은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (34)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (34)
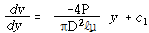
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (34-1)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (34-1)
이 방정식을 두 번 적분하고 경계조건 ![]() ( y =0)과
( y =0)과 ![]() =0( y = d )을 사용하여
=0( y = d )을 사용하여
![]() 일 때
일 때 ![]() 를 식 (34-1)에 대입하면
를 식 (34-1)에 대입하면
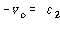
![]() 일 때
일 때 ![]() 를 식 (34-1)에 대입하면
를 식 (34-1)에 대입하면
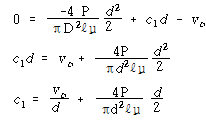
그러므로
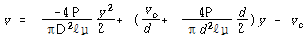
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (35)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – (35)
환형공간을 통한 유체의 유량은![]() =0과
=0과 ![]() = d 사이의 유량을 적분함으로써 구할 수 있다.
= d 사이의 유량을 적분함으로써 구할 수 있다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – (36)
– – – – – – – – – – – – – – – – – – – – – – – – (36)
단위초당 환형공간을 통하여 흐르는 유체의 체적은 피스톤에 의하여 대치되는 단위초당의 체적과 같아야만 한다. 즉, 피스톤의 속도는 체적유량을 피스톤 면적으로 나눈 것과 같아야 한다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (37)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (37)
(37)과 (36)으로 부터
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (38)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (38)
힘을 ![]() 로 표시하면 감쇠상수 c는
로 표시하면 감쇠상수 c는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (39)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (39)
이 된다.
8.1.4.3 減衰의 重要性 (Importance of Damping)
시스템에서 높은 감쇠값이 바람직하다는 것은 분명하다. 그러나 어떤 경우에는 감쇠가 역효과를 가질 수 있다. 만일 시스템의 감쇠계수가 영이라면 공진 주파수에서 진동진폭은 무한대에 이를 것이다. 물론 어느 정도의 감쇠가 항상 존재하므로 이런 일은 결코 발생하지 않는다.
마찰감쇠 또는 Coulomb 감쇠로부터의 과도한 감쇠로 인해 시스템이 그 공진 주파수에서 진동하도록 실제로 가진할 수 있다. 예를 들면 단순한 음료수 유리잔의 고유 진동수는 축축한 손가락으로 유리잔을 문질러도 가진될 수 있다. 마찬가지로 슬리브 베어링에 윤활유가 없으면 베어링, 축 및 관련 기계 부품의 공진을 가진할 만큼 충분한 마찰을 일으킬 수 있다. 이것은 Dry 베어링과 관련한 특이한 “소음(Squeal)”을 수반한다. 이로 인한 진동은 회전속도에 비하여 전형적으로 대단히 높은 주파수를 가지나 정상적으로는 회전 주파수의 배수 관계는 아니다. 윤활 부족에 의한 회전축과 정지한 베어링간의 과도한 마찰은 축이 베어링 표면을 따라 오르거나 구를 때 베어링 내에서 축이 선회하도록 할 수 있다.
축의 선회방향은 축의 회전 방향과 반대이며 선회 진동주파수는 축의 회전속도를 축의 원주로 나눈 값에 접근한다. 이것은 축의 회전수에 비하여 상당히 낮은 진동주파수이며, 통상적으로 축의 회전수의 정확한 약수는 아니다. 그러나 그 진동은 대단히 극렬하고 파괴적이어서 거의 직접적인 기계 손상을 일으킨다.
유막 베어링에서 유막에 의해 생긴 점성감쇠와 같은 정적인 감쇠는 일반적으로 기계가 기동 또는 정지중 로터의 임계속도를 통과할 때 로터 진동 진폭을 최소화하기 위해서는 바람직하다. 그러나 임계속도를 지나는 로터 진동이 상당히 극렬하면 베어링 내의 축진동은 이 점성감쇠를 크게 감소시킬 만큼 유막을 깨트릴 수 있다. 이런 일이 발생하면 임계속도에서 축 진동 진폭은 더욱 증폭되어 통상 가공할 만한 결과를 초래한다. 또한 이런 유막파괴는 로터의 임계상태를 더욱 가진하도록 베어링과 회전축간의 마찰감쇠를 초래할 수 있다. 이러한 이유 때문에 로터의 임계속도 이상에서 운전하고 있는 기계의 정지시 진동치는 정상적인 베어링 간극에 비하여 여유가 있다. 임계속도를 지나서 정지될 때 로터 진동은 증폭될 것이며 또 감속율이 때로는 제어되지 못하기 때문에 너무 높게 책정된 “Trip”치로 인해 정지시 파괴적인 진동치를 가져올 수 있다.
정적인 감쇠는 바람직하지만 회전체의 감쇠는 심각한 문제점을 일으킬 수 있다. 기록된 사고의 예를 들면 운전 속도보다 훨씬 아래에 있는 임계주파수와 똑같은 주파수에서 터빈 로터가 극렬하게 진동하고 있는 것이 발견되었다. 그 원인은 터빈과 감속기 간의 커플링에서의 윤활 부족이었음이 판명되었다. 커플링의 윤활 부족으로 인해 커플링 Spline과 Spool 기어간의 마찰을 초래하였다. 이 마찰은 축축한 손가락으로 유리잔을 문지르므로 인해 유리잔의 고유 진동수가 가진된 것처럼 로터의 고유 진동수를 가진 시켰다. 이러한 장면을 본 관찰자에 의하면 커플링 내에서 발생한 마찰은 커플링이 빨갛게 달아오를 만큼 상당히 심각하였다고 한다. 다른 예에서 터빈 제작자는 특별히 설계된 터빈 로터에서 진동 문제를 경험하였는데 여기서도 역시 진동 분석 결과 진동주파수는 회전속도 주파수 보다 훨씬 아래에 있는 로터의 임계속도 주파수이었음이 발견되었다. 이 경우 터빈 Wheel은 축에 열박음한 것인데 불충분한 끼워 맞춤으로 인해 운전 온도에서 Wheel이 축상에서 움직이게 되었음이 확인되었다. 축상에서 Wheel의 이동에 의한 마찰은 바이올린의 활이 줄에서 당겨질 때 고유 주파수가 가진되는 것과 같이 로터의 고유 주파수를 가진 시킨다.
원하지 않는 마찰이나 Coulomb 감쇠의 또 다른 예는 공작 기계에서 절삭 공구와 가공물간에서 발생된 마찰이다. 절삭 공구가 무디거나 절삭 이송율이나 깊이가 과도하면 이로 인한 마찰은 가공 물체, 공구, Tool Holder 및 기타 물체의 고유 주파수를 가진할 수 있다. 물론 그 결과는 Chattering 현상이 있어 가공표면 정도가 불량하게 된다. 여기서 발생한 진동주파수가 전형적으로 불평형, 벨트 문제, 기어나 베어링 주파수 등과 같은 다른 기계 문제점의 주파수와 관련이 없기 때문에 이 문제를 규명하는 것은 아주 간단하다.
8.1.4.4 減衰處理의 形態 (Types of Damping Treatments)
표면 감쇠 처리형태에는 크게 Free-Layer Type과 Constrained-Layer Type 2가지가 있다. 그림 8-16은 Free-Layer처리를 보여주고 있으며 이는 Base Structure에 적용한 단층의 점탄성 재질(Viscoelastic Material)로 되어 있고, 점탄성 재질의 변형을 유도하게 하는 Base Structure의 굽힘 진동에 따라 다르다. 즉 이것은 매 진동 Cycle과 더불어 인장 및 압축하도록 놓인 Metal에 따라 다르다. 이렇게 되면 Base Structure로부터의 탄성 응력하에 있는 재질의 인장 및 압축 결과로써 Energy는 발산된다. 그림 8-16의 경우 일정한 두께의 감쇠재(3/16 in)를 두께가 1/32 in에서 1/2 in까지 각기 다른 철판 위에 적용하였다. 그림 8-16은 3.5항에서 설명될 식 (128)로 정의된 시스템의 Loss Factor(η)에 어떻게 영향을 미쳤는지를 보여주고 있다. 그림 8-16은 감쇠 처리로 철판 두께를 감소시킴에 따라 크게 효과를 준 것을 보여준다. 또한 Loss Factor가 최고인 곳에 최적의 온도가 있었고, 이것은 철판의 두께에 따라 변화되었음을 보여준다. 이것은 감쇠재를 사용하는 경우 일반적인 사항이다. 실제로 감쇠처리를 선정할 때 일련의 처리형태 모두를 사용할 수 있다.
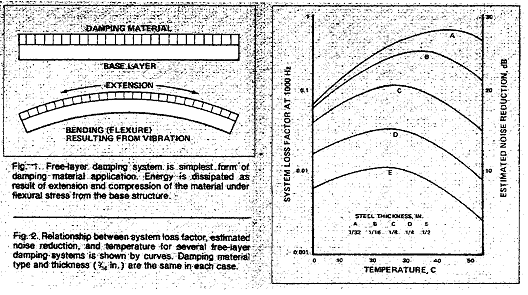
그림 8-16 Free Layer Damping
그림 8-17은 여러 제작자가 공급한 감쇠재에 대한 성능 자료이다. 이들은 Damping Loss Factor(Y)대 주파수를 나타낸 곡선을 가지고 있다. 감쇠 능력이 온도에 따라 어떻게 변화하는지에 대해 주목하라. 예를 들면 EAR C-203이라는 감쇠 처리중 하나를 보면 이 재질은 통상 그 재질이 적용된 표면 온도가 대략 4 ℃~16 ℃(40 ˚F~60 ˚F)와 60 ℃~71 ℃(140 ˚F~160 ˚F)일 때 (여기서 Loos Factor Y=0.60) 400 ㎐ 주파수에서 효과적이다. 한편 이 재질은 Loos Factor가 0.2이하일 때 -4 ℃이하나 71 ℃이상에서는 거의 감쇠효과가 없다. 400 ㎐ 주파수에서 약 121 ℃(250 ˚F)의 높은 표면 온도에 대해서는 그림 8-17은 Soundcoat DYAD609가 좋은 것으로 보여주고 있다.
일반적으로 최적의 감쇠를 주기 위하여서는 먼저 현존하는 주종 주파수를 알아야 한다. 그리고는 감쇠처리가 적용되는 곳의 온도를 알아야 한다. 그림 8-17과 같은 도표를 사용하여 이것을 알고나서 운전조건하에서 최적의 감쇠 처리형태를 선택해야 한다. 또 하나 중요한 것은 구조물위에 감쇠 처리를 위치시킬 때 가장 효과적이 되기 위해서는 진동진폭이 가장 높은 곳에 위치 시켜야 한다.
그림 8-18은 Constrained-Layer Damping이라고 불리는 감쇠의 다른 형태를 보여준다. 이 경우 Constrained Layer 처리는 2개의 층 즉, 하나는 탄 점성 재질 층, 또 하나는 상당히 강성이 있는 재질 층(통상 Sheet Metal)으로 되어 있다. 이들 각각은 기계 표면에 접착되어 있다. Base Structure의 굽힘 진동은 추가된 Sheet Metal층이 탄점성층의 외부 경계상에 주어지는 구속 때문에 탄점성 재질의 전단 변형을 일으킨다. 이 접착물은 전단 강성을 가져야한다. 이 접착물의 전단 변형은 효과를 감소시키는 감쇠층의 변형을 감소시킨다. 일반적으로 Constrained Layer를 가지는 감쇠 시스템은 진동 에너지가 감쇠재의 변형을 통해서 뿐만 아니라 Constraining Layer의 접착물을 통해서도 발산되기 때문에 Free-Layer 처리보다 크게 효과적이다. 또한 Constrained -Layer Damping은 구조물에 강도를 추가하여 고유주파수 이하의 영역에서도 진동을 낮게 할 수 있다. 왜냐하면 이 영역은 주로 강성에 의해 제어되기 때문이다. 또한 그림 8-18은 Constrained Layer처리가 가장 효과적인 상태가 되는 최적의 온도 및 주파수 영역을 가지는 온도에 종속됨을 보여준다.
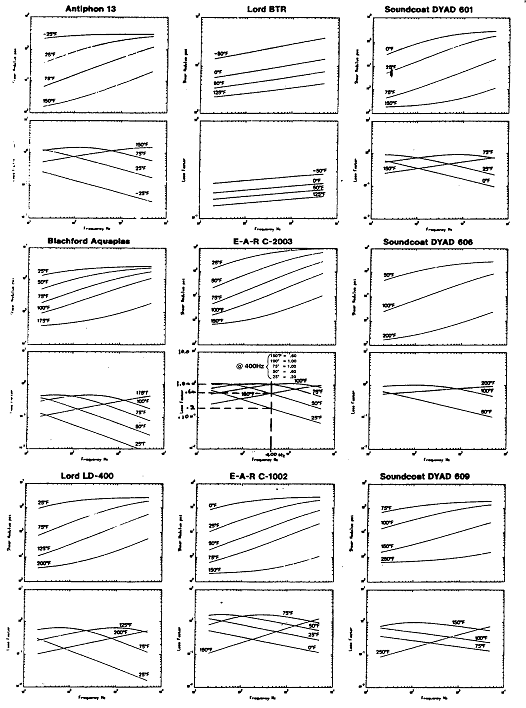
그림 8-17 여러 감쇠재의 물리적 특성
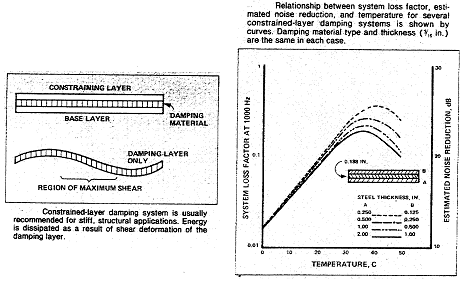
그림 8-18 Constrained Layer Damping
(최종적인 시스템 감쇠에 온도, 주파수 및 두께가 미치는 영향)
8.2 1 자유도계의 자유진동 (Free Vibration of Single Degree of Freedom Systems)
다수의 기계와 구조물계는 1 자유도계로 단순화할 수 있다. 대부분의 실제 시스템에 있어서 질량은 분산되어 있으나 질량이 한 점에 집중된 것으로 보고 그 거동을 개략화할 수 있다.
8.2.1 비감쇠 병진계의 자유진동 (Free Vibration of an Undamped Translational System)
8.2.1.1 뉴튼의 運動 第2法則을 利用한 運動方程式
(Equation of Motion Using Newton’s Second Law of Motion)
(1) 수평의 스프링-질량 시스템
그림 8-19(a)의 비감쇠 1 자유도계를 생각해 보자. 질량은 마찰이 없는 롤러에 지지되어 있고 수평방향으로 병진운동을 한다. 스프링의 당겨지지 않은 상태의 길이는![]() 이다. 질량을 정지상태로부터
이다. 질량을 정지상태로부터 ![]() 의 거리만큼의 위치에 놓으면 그림 8-19(c)에서와 같이 스프링력
의 거리만큼의 위치에 놓으면 그림 8-19(c)에서와 같이 스프링력 ![]() 를 야기 시킨다. 뉴튼의 제2법칙에 의하면
를 야기 시킨다. 뉴튼의 제2법칙에 의하면
질량×가속도 = 질량에 가해진 합성력 – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (40)
식 (40)을 m 에 적용하면 다음의 운동방정식을 세울 수 있다.
![]() 또는
또는 ![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (41)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (41)
![]() 에서 -의 의미는
에서 -의 의미는 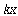 의 힘의 운동방향이
의 힘의 운동방향이 ![]() 의 힘의 운동방향과 정반대이기 때문에 등호를 성립시키기 위해서 -를 삽입하여야 하기 때문임. 또한 결과적으로 우변의 항을 좌변으로 옮긴
의 힘의 운동방향과 정반대이기 때문에 등호를 성립시키기 위해서 -를 삽입하여야 하기 때문임. 또한 결과적으로 우변의 항을 좌변으로 옮긴 ![]() 는 χ의 어느 위치에서나 합력은 “0”임을 의미한다. 여기서
는 χ의 어느 위치에서나 합력은 “0”임을 의미한다. 여기서 ![]() 는 질량의 가속도이다.
는 질량의 가속도이다.
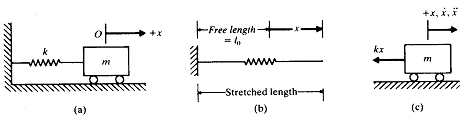
그림 8-19 수평의 스프링-질량시스템
(2) 수직의 스프링-질량 시스템
그림 8-20(a)에서 보는 바와 같은 스프링-질량시스템을 생각해보자. 질량 m 은 스프링의 아래쪽 끝에 매달려 있고 스프링의 다른 한쪽 끝은 벽에 고정되어 있다. 정지 상태에서 질량은 정적 평형위치라 불리는 위치에 매달려 있고 위쪽으로 향하는 스프링력이 아래쪽으로 향하는 중력과 정확하게 균형을 이루고 있다. 이 위치에서 스프링의 길이는![]() 이며 (
이며 (![]() 는 정적처짐) 질량 m 의 무게 W로 인한 신장량이다. 그림 8-20(a)에서 정적평형인 경우
는 정적처짐) 질량 m 의 무게 W로 인한 신장량이다. 그림 8-20(a)에서 정적평형인 경우
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (42)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (42)
여기서 g 는 중력가속도. 질량이 정적평형 위치에서![]() 만큼 움직이면 스프링력은 그림 8-20(c)에서와 같이
만큼 움직이면 스프링력은 그림 8-20(c)에서와 같이![]() 가 된다. 뉴튼의 운동 제2법칙을 질량 m 에 적용하면
가 된다. 뉴튼의 운동 제2법칙을 질량 m 에 적용하면
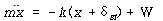
가 되며 -는 앞에서 설명한 바와 같은 의미이고 +W의 의미는 항상 지구 중심방향으로 W의 힘이 스프링에 작용하고 있음을 의미한다. 지구 중력에 의한 W는 항상 지구 중심방향으로 향하기 때문에 ![]() 와 W는 서로 상쇄된다.
와 W는 서로 상쇄된다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (43)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (43)
식 (41)과 식 (43)이 동일하다는 것을 알 수 있다. 즉 질량이 수직방향으로 움직일 때는 정적 평형 위치로부터![]() 를 측정하기 때문에 무게의 영향을 무시할 수 있다.
를 측정하기 때문에 무게의 영향을 무시할 수 있다.
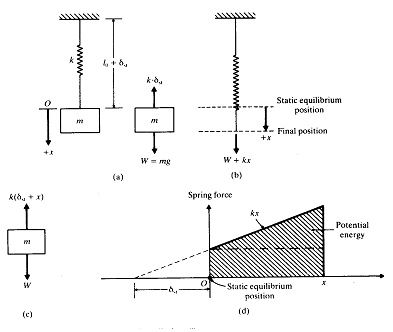
그림 8-20 수직방향의 스프링-질량시스템
8.2.1.2 에너지 保存의 原理를 利用한 運動方程式
(Equation of Motion Using the Principle of Conservation of Energy)
식 (41)은 또한 에너지보존의 원리를 이용하여 유도할 수 있다. 이 원리를 적용하기 위하여 우선 감쇠로 인한 에너지 소멸이 없어야 하며 그림 8-19(a)는 보존적이라고 한다. 진동중 시스템의 에너지는 일부가 운동에너지이고 나머지는 위치에너지이다. 운동에너지 T는 그 속도로 인하여 축적되고 위치에너지 U는 탄성변형으로 인하여 스프링에 축적된다. 에너지보존의 법칙에 따라
T + U = 일정 혹은 ![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (44)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (44)
운동 및 위치에너지는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (45)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (45)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (46)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (46)
식 (45) 및 식 (46)을 식 (44)에 대입하고 미분을 하게되면
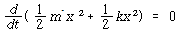
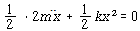
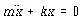
8.2.1.3 運動方程式의 解 (Solution of Motion Equation)
식 (41)의 해는 다음과 같이 가정함으로써 구할 수 있다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (47)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (47)
C 와 s는 결정되어야 할 상수이며
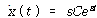
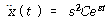
식 (41)에 대입하면
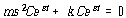
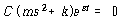
C 및 ![]() 는 0이 아니므로
는 0이 아니므로
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (48)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (48)
가 되고
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (49)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (49)
![]() 이며
이며
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (50)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (50)
식 (48)은 식 (41)의 미분방정식에 대응하는 보조 혹은 특성방정식이라 불린다.
식 (49)에 주어진 s의 두 값은 특성방정식의 근이며 문제의 고유치 혹은 특성치라고 알려져 있다.
s의 두 값은 식 (48)을 만족시키기 때문에 식 (41)의 일반해는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (51)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (51)
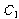 및
및 ![]() 는 상수이다.
는 상수이다.
오일러의 공식 ![]() 를 사용하여 식 (51)을 다시 쓰면
를 사용하여 식 (51)을 다시 쓰면
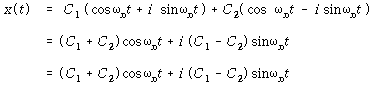 – – – – – – – – – – – – – (52)
– – – – – – – – – – – – – (52)
![]() 및
및 ![]() 는 새로운 상수이다. 상수
는 새로운 상수이다. 상수![]() 및
및![]() 혹은
혹은![]() 및
및![]() 는 시스템의 초기조건으로부터 결정되다. 만약, 변위
는 시스템의 초기조건으로부터 결정되다. 만약, 변위![]() 및 속도
및 속도 ![]() 가 t =0에서
가 t =0에서 ![]() 및
및 ![]() 로 주어지면 식 (52)로 부터
로 주어지면 식 (52)로 부터
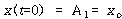
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (53)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (53)
그러므로, ![]() 및
및 ![]() 이 된다. 식 (53)의 초기조건에 좌우되는 식 (41)의 해는
이 된다. 식 (53)의 초기조건에 좌우되는 식 (41)의 해는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (54)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (54)
식 (52)는 다음과 같은 표현을 도입함으로써 다른 형태로 나타낼 수 있다.
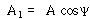
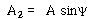
여기서 A 및 ψ는 새로운 상수이며 ![]() 및
및 ![]() 의 항으로 표시될 수 있다.
의 항으로 표시될 수 있다.
![]() = 진폭
= 진폭
![]() = 위상각
= 위상각
이를 식 (52)에 대입하면 그 해는
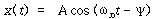
[예제] 10 ㎏의 질량을 매달 때 스프링-질량시스템이 10 rad/s(약 1.6 ㎐)의 진동수를 갖도록 헬리컬 스프링을 설계하여라.
[해] 고유진동수의 정의로부터 스프링은 강성이
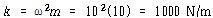
이 되어야 한다. 헬리컬 스프링의 강성은
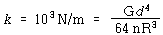
이 된다. 위의 식은 어떠한 설계를 하기 위한 출발점이 된다. 선택할 수 있는 것은 사용할 재료(즉, 여러 가지 값의 G), 재료의 직경 d, 코일의 반지름 R, 그리고 감은 수 n 등이다. G와 d 는 물론 얻을 수 있는 재료에 의해 제한되고 n은 정수가 되도록 제한되며, R은 기기의 크기에 따라 요구사항에 의한 제한을 받을 수 있다. 여기서 1 ㎝ 직경의 강철을 사용할 수 있다고 가정한다. 강철의 전단탄성계수는 약
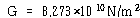
이 되므로 강성공식은
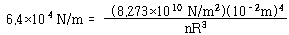
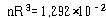
이 된다. 코일의 반지름을 10 ㎝로 선택하면 감은 수는
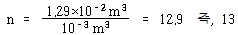
이 되어야 한다. 그러므로 1 ㎝ 직경의 강철을 반경 10 ㎝로 13회 감으면, 스프링은 원하는 강성을 갖고 10 ㎏의 질량은 약 10 rad/s로 진동할 것이다.
8.2.2 비감쇠 비틀림 시스템의 자유진동 (Free Vibration of Undamped Torsional System)
만약, 하나의 강체가 특정한 축에 관해서 진동할 때 결과적인 운동을 비틀림 진동이라 한다. 이 경우에 강체의 변위는 각좌표의 항으로 측정된다. 비틀림 진동 문제에 있어서 복귀 모멘트는 탄성체의 비틀림 혹은 힘이나 짝힘의 불평형 모멘트 때문일 것이다.
그림 8-21은 극관성 질량 모멘트 ![]() 인 디스크가 원형의 축 한쪽 끝에 설치되어 있고 다른 끝은 고정되어 있다. 축의 중심선에 대해 θ만큼 디스크를 각회전 시킨다 (θ는 축의 비틀림 각도를 나타낸다).
인 디스크가 원형의 축 한쪽 끝에 설치되어 있고 다른 끝은 고정되어 있다. 축의 중심선에 대해 θ만큼 디스크를 각회전 시킨다 (θ는 축의 비틀림 각도를 나타낸다).
원형축의 비틀림 이론으로부터
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (55)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (55)
![]() 는 비틀림θ를 일으키기 위한 토오크, G는 전단탄성계수, ℓ는 축의 길이, J는 축단면의 극관성모멘트이며
는 비틀림θ를 일으키기 위한 토오크, G는 전단탄성계수, ℓ는 축의 길이, J는 축단면의 극관성모멘트이며
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (56)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (56)
d 는 축의 직경을 의미한다. 만약, 디스크가 평형위치에서 θ만큼 움직였다면 축은 크기 ![]() 의 복귀 토오크를 제공한다. 그러므로, 축은 비틀림 스프링으로 거동하고 비틀림 스프링상수는
의 복귀 토오크를 제공한다. 그러므로, 축은 비틀림 스프링으로 거동하고 비틀림 스프링상수는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (57)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (57)
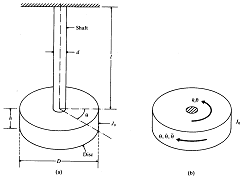
그림 8-21 디스크의 비틀림 진동
8.2.2.1 運動方程式 (Equation of Motion)
디스크의 2축에 관한 각운동 방정식은 뉴튼의 제2법칙 혹은 에너지 보존 원리를 사용하여 유도할 수 있다. 디스크의 자유물체 선도를 고려하여 뉴튼의 제2 운동법칙을 적용함으로써 운동방정식을 유도할 수 있다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (58)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (58)
식 (58)은 만약 극관성 질량모멘트![]() , 각 변위θ, 및 비틀림 스프링 상수
, 각 변위θ, 및 비틀림 스프링 상수![]() 가 질량 m , 변위
가 질량 m , 변위![]() 및 선형스프링 상수
및 선형스프링 상수![]() 로 각각 대치된다면 식 (41)과 동일함을 보여준다. 그러므로 비틀림 시스템의 고유각 주파수는
로 각각 대치된다면 식 (41)과 동일함을 보여준다. 그러므로 비틀림 시스템의 고유각 주파수는
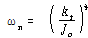 – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (59)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (59)
주기와 진동주파수는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (60)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (60)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (61)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (61)
이 비틀림 시스템에서 다음의 관점들에 주의하라.
① 디스크를 지지하고 있는 축의 단면이 원형이 아닌 경우는 적절한 비틀림 스프링계수를 이용하여야 한다.
② 디스크의 극관성 질량모멘트는
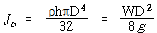
ρ는 질량밀도, h는 두께, D는 직경, 그리고 W는 디스크의 무게이다.
③ 그림 8-21의 비틀림 스프링-관성시스템은 비틀림 진자로서 언급된다. 비틀림 진자의 가장 중요한 적용중의 하나는 기계식 시계이며 라체트와 폴은 작은 비틀림 진자의 규칙적인 진동을 침의 움직임으로 변환하는 것이다.
8.2.2.2 解 (Solution)
식 (58)의 일반해는 식 (41)의 경우와 같이 구해진다.
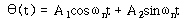 – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (62)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (62)
![]() ,
, ![]() 는 초기조건
는 초기조건
![]() ,
, ![]() – – – – – – – – – – – – – – – – – – – – – – – (63)
– – – – – – – – – – – – – – – – – – – – – – – (63)
로부터 구해지며
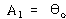
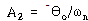 – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (64)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (64)
로 된다.
식 (62)도 또한 단순조화운동을 나타낸다.
8.2.3 점성 감쇠계의 자유진동 (Free Vibration with Viscous Damping)
8.2.3.1 運動方程式 (Equation of Motion)
점성감쇠력 F는 속도![]() 에 비례하며 다음과 같이 표현된다.
에 비례하며 다음과 같이 표현된다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (65)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (65)
c는 감쇠상수 혹은 점성감쇠계수이며 음의 부호는 감쇠력이 속도방향과 반대임을 의미한다. 점성댐퍼가 있는 1 자유도계가 그림 8-22에 제시되어 있다.
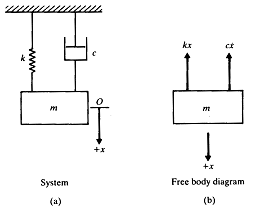
그림 8-22 점성댐퍼가 있는 1 자유도계
만약 질량 m 가 평형위치로부터 x 만큼 이동되었다면 뉴튼의 법칙에 따라 다음과 같이 운동방정식이 유도된다.
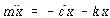
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (66)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (66)
8.2.3.2 解 (Solution)
식 (66)의 해를 구하기 위해 다음과 같은 형태의 해를 가정한다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (67)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (67)
여기서 c 와 s는 결정되지 않은 상수이다. 이 함수를 식 (67)에 대입하면 다음과 같은 특성방정식을 구하게 된다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (68)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (68)
그 근은
![]() – – – – – – – – – – – – – – – – – – – (69)
– – – – – – – – – – – – – – – – – – – (69)
이 근은 2개의 해를 제시하며
![]() 및
및 ![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (70)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (70)
식 (66)의 일반해는 두 해의 선형조합으로 주어진다.
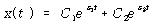
임계 감쇠상수와 감쇠비 : 임계 감쇠 ![]() 는 식 (69)의 근호내에 있는 감쇠상수 c가 0이 되는 것으로 정의한다.
는 식 (69)의 근호내에 있는 감쇠상수 c가 0이 되는 것으로 정의한다.
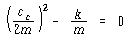
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (71)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (71)
어떠한 감쇠 시스템에서 감쇠비 ζ는 임계 감쇠상수에 대한 감쇠상수의 비로서 나타낸다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (72)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (72)
식 (71)과 식 (72)으로부터
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (73)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (73)
즉
![]() (74)
(74)
![]() – – – – – – – – – – – – – – – – – – – – – – (75)
– – – – – – – – – – – – – – – – – – – – – – (75)
근![]() 과
과 ![]() 의 특성 및 식 (75)의 거동은 감쇠의 크기에 좌우된다. ζ=0의 경우는 앞 절에서 설명되었기 때문에 ζ≠0로 가정하고 다음의 3가지 경우에 대해 생각해 보기로 한다.
의 특성 및 식 (75)의 거동은 감쇠의 크기에 좌우된다. ζ=0의 경우는 앞 절에서 설명되었기 때문에 ζ≠0로 가정하고 다음의 3가지 경우에 대해 생각해 보기로 한다.
경우 1 부족감쇠시스템 (ζ<1 혹은 ![]() 혹은
혹은 ![]() )
)
이와 같은 경우 ![]() 은 음이고 근
은 음이고 근 ![]() 는 다음과 같이 표현된다.
는 다음과 같이 표현된다.
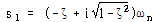
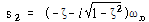
식 (75)는 다음과 같이 다른 형태로 표현할 수 있다.
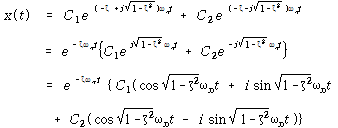
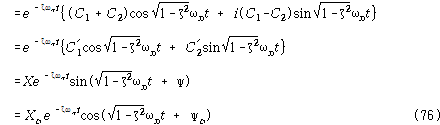
여기서![]() , (χ,ψ) 및
, (χ,ψ) 및![]() 는 임의상수이며 초기조건으로부터 결정된다.
는 임의상수이며 초기조건으로부터 결정된다.
초기조건 ![]() 와
와 ![]() 일 때,
일 때, ![]() 및
및 ![]() 는 다음과 같이 구해진다.
는 다음과 같이 구해진다.
![]() 에 t =0을 대입하면
에 t =0을 대입하면
![]() 가 되고, 위 식을 미분하면
가 되고, 위 식을 미분하면
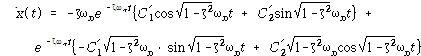
가 되고 t =0을 대입하면,
![]() 가 된다.
가 된다.
![]() 를 위 식에 대입하면
를 위 식에 대입하면
![]() 가 되고 결과적으로
가 되고 결과적으로
∴ ![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (77)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (77)
가 된다.
![]() 를 원식에 대입하면
를 원식에 대입하면
![]() – – – – – – – – – – – – (78)
– – – – – – – – – – – – (78)
상수 (Χ, ψ) 및 (![]() )는
)는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (79)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (79)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (80)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (80)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (81)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (81)
식 (78)에 의해 표시되는 운동은 각 주파수 ![]() 의 조화운동이지만
의 조화운동이지만 ![]() 로 인하여 진폭은 시간의 경과와 더불어 지수적으로 감소한다 (그림 8-23).
로 인하여 진폭은 시간의 경과와 더불어 지수적으로 감소한다 (그림 8-23).
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (82)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (82)
![]() 는 감쇠진동의 고유 주파수라고 하며 항상 비감쇠 고유진동수
는 감쇠진동의 고유 주파수라고 하며 항상 비감쇠 고유진동수![]() 보다는 작다.
보다는 작다.
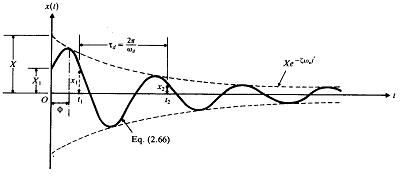
그림 8-23 부족감쇠의 해
감쇠량의 증가에 따른 감쇠 진동 주파수의 감소가 그림 8-24에 나타나 있다.
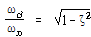
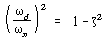
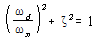
부족감쇠의 경우가 기계진동의 연구에 있어 가장 중요하며 그 이유는 유일하게 진동운동을 하기 때문이다.
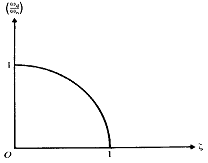
그림 8-24 감쇠의 크기에 따른 ωd의 변화
경우2 : 임계 감쇠 시스템 (ζ=1 혹은 ![]() 혹은
혹은 ![]() )
)
식 (69)에서![]() 이므로 2개의 근
이므로 2개의 근![]() 는 같고
는 같고
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (83)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (83)
이 된다.
중근이기 때문에 식 (68)의 해는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (84)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (84)
초기조건![]() 와
와 ![]() 를 적용하여
를 적용하여
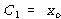
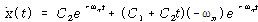
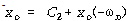
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (85)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (85)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (86)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (86)
식 (86)에 의해 표현되는 운동은 비주기적이다.
t = ∞이면 ![]() =”0″으로 되기 때문에 운동은 결국 그림 8-25에서 나타낸 바와 같이 진폭이 0으로 되어 사라진다.
=”0″으로 되기 때문에 운동은 결국 그림 8-25에서 나타낸 바와 같이 진폭이 0으로 되어 사라진다.
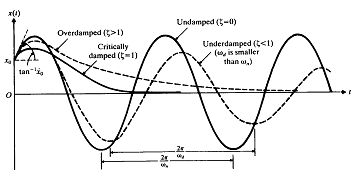
그림 8-25 감쇠의 형태에 따른 운동의 비교
경우3 : 과감쇠 진동시스템 (ζ>1 혹은 ![]() 혹은
혹은![]() )
)
![]() >0 때문에
>0 때문에 ![]() 및
및 ![]() 는 실수이며
는 실수이며
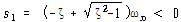
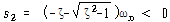
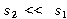
![]() – – – – – – – – – – – – – – – – – – – – – – – (87)
– – – – – – – – – – – – – – – – – – – – – – – (87)
초기조건 ![]() 와
와 ![]() 로부터
로부터 ![]() 과
과 ![]() 가 구해진다. 즉,
가 구해진다. 즉,
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (88)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (88)
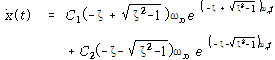
![]() – – – – – – – – – – – – – – – – – – – – – (89)
– – – – – – – – – – – – – – – – – – – – – (89)
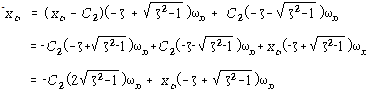
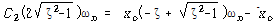
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (90)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (90)
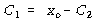
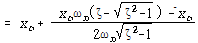
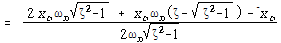
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (91)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (91)
식 (87)로부터 이 시스템에 가해진 초기조건에는 관계없이 주기적인 운동을 함을 알 수 있다. 근 ![]() ,
, ![]() 는 음이기 때문에 운동은 시간의 경과에 따라 지수적으로 감소하고 사라진다 (그림 8-25).
는 음이기 때문에 운동은 시간의 경과에 따라 지수적으로 감소하고 사라진다 (그림 8-25).
8.2.3.3 代數 減衰率 (Logarithmic Decrement)
대수 감쇠율은 자유감쇠진동의 진폭이 감소하는 비를 나타낸다. 어떤 2개의 연속되는 진폭의 자연대수비로서 정의된다. ![]() 과
과 ![]() 를 2개의 연속되는 진폭에 대응하는 시각을 나타낸다고 하면 각각의 시각에서의 부족감쇠시스템의 진폭은 다음과 같이 된다.
를 2개의 연속되는 진폭에 대응하는 시각을 나타낸다고 하면 각각의 시각에서의 부족감쇠시스템의 진폭은 다음과 같이 된다.
![]() 은 임의의 시간 에서의 진동진폭이고
은 임의의 시간 에서의 진동진폭이고 ![]() 는
는 ![]() 에서의 진동진폭이므로
에서의 진동진폭이므로
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (92)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (92)
가 된다.
여기서 ![]() (
(![]() : 감쇠진동의 주기)이다.
: 감쇠진동의 주기)이다.
![]() 와 같게 되므로 식 (92)는
와 같게 되므로 식 (92)는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (93)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (93)
대수 감쇠율 δ는 식 (93)으로부터
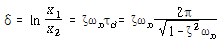
![]() – – – – – – – – – – – – – – – – – (94)
– – – – – – – – – – – – – – – – – (94)
감쇠가 작을 경우 식 (94)는 간략하게 다음과 같이 나타낼 수 있다.
δ = 2πζ (만약 ζ << 1인 경우) – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (95)
그림 8-26은 ζ에 따른 대수 감쇠율 δ의 변화를 보여준다. ζ= 0.3까지의 δ값은 식 (94)과 식 (95)에서 거의 동일한 값을 나타낸다.
대수감쇠율은 무차원이고 실제적으로 무차원 감쇠비 ζ의 다른 형태이다. 일단 δ가 기지의 값이라면 식 (94)로부터 ζ를 구할 수 있다.
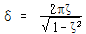
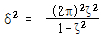
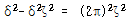
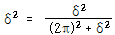
∴![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (96)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (96)
만약 식 (94) 대신에 식 (95)를 사용한다면
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (97)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (97)
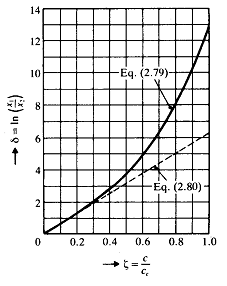
그림 8-26 감쇠값에 따른 대수감쇠율의 변화
주어진 진동 시스템에서 감쇠값이 알려져 있지 않으면 실험적으로 두 개의 연속되는 변위 ![]() 과
과 ![]() 를 측정함으로서 구할 수 있다.
를 측정함으로서 구할 수 있다. ![]() 과
과 ![]() 의 자연대수비를 취함으로써 δ를 얻을 수 있다.
의 자연대수비를 취함으로써 δ를 얻을 수 있다.
식 (96)을 사용함으로써 감쇠비 ζ를 계산할 수 있다. 실제적으로는 감쇠비 ζ는 수 개의 사이클에 의해 분리된 처음과 끝의 두 변위를 측정함으로써도 구할 수 있다.
만약 ![]() 과
과 ![]() 이 시간
이 시간 ![]() 과
과 ![]() 에 상응하는 진폭이라면
에 상응하는 진폭이라면
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (98)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – (98)
어떤 두개의 연속된 변위는 한 사이클에 의해 분리되기 때문에
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (99)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (99)
식 (98)은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (100)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (100)
식 (100)과 식 (94)로부터
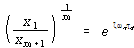
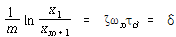
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (101)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (101)
[예제] 부족감쇠의 충격흡수기가 자동차에 설계되었다. 초기진폭은 그림 8-27에서 보는 바와 같이 첫째 반 사이클 동안에 ![]() 로 감쇠된다. 차의 질량은 500 ㎏이고 진동주기는 1초이다. 충격흡수기에서 필요한 강성 및 감쇠상수를 구하라. 또한, 간극이 250 ㎜라면 시스템의 Rubber Base를 타격하는 최소의 초기속도를 구하라.
로 감쇠된다. 차의 질량은 500 ㎏이고 진동주기는 1초이다. 충격흡수기에서 필요한 강성 및 감쇠상수를 구하라. 또한, 간극이 250 ㎜라면 시스템의 Rubber Base를 타격하는 최소의 초기속도를 구하라.
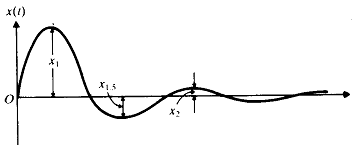
그림 8-27
[해]
![]() ,
, ![]() 이 되며 대수감쇠율
이 되며 대수감쇠율
![]() – – – – – – – – – – – – – – – – – – – – – (102)
– – – – – – – – – – – – – – – – – – – – – (102)
식 (102)로부터 ζ=0.4037, 진동주기는 1 sec이므로
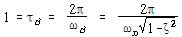
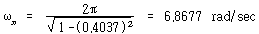
임계감쇠상수는
![]() = 2(500) (6.8677) = 6887.7 N•s/m
= 2(500) (6.8677) = 6887.7 N•s/m
감쇠상수는
![]() = (0.4037)(6867.7) = 2772.4905 N•s/m
= (0.4037)(6867.7) = 2772.4905 N•s/m
강성은
![]() = (500)(6.8677)2 = 23582.652 N/m
= (500)(6.8677)2 = 23582.652 N/m
질량의 변위는 시각 ![]() 에서 최대값을 갖으며
에서 최대값을 갖으며
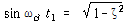
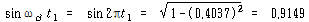
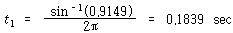
최대점을 통과하는 그림 8-23의 점선의 χ값은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (103)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (103)
χ = 250 ㎜이므로 식 (103)은
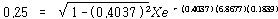
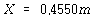
질량의 속도는 변위를 미분함으로써 얻을 수 있으며
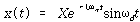
![]() – – – – – – – – – – – – – – – – – – – – (104)
– – – – – – – – – – – – – – – – – – – – (104)
t = 0 일 때 식 (104)은
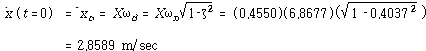
8.3 1 자유도계의 강제진동 (Forced Vibration of Single Degree of Freedon Systems)
8.3.1 개요 (Introduction)
어떤 동적 시스템은 강제 혹은 여기함수라 불리는 일종의 외력 혹은 여기력에 의해 지배된다. 이 여기력은 보통 시간 의존성이며 조화적, 비조화적이나 주기적, 비주기적 혹은 본질적으로 랜덤일 수도 있다. 조화 여기에 대한 시스템의 응답을 조화응답이라한다. 갑자기 가해진 비주기적인 여기에 대한 시스템의 응답을 과도응답이라 한다. 여기서는 조화여기에 의한 1자유도계의 동적응답을 논의한다. 가장 일반적인 형태의 조화여기는 ![]() 혹은
혹은 ![]() 의 형태를 가지며
의 형태를 가지며 ![]() 는 상수로써 여기 진폭을 의미하고 ω는 조화진동의 주파수, ψ는 위상각이다. ψ의 값은 t=0에서의 F(t) 값에 의존하며 보통 0이다.
는 상수로써 여기 진폭을 의미하고 ω는 조화진동의 주파수, ψ는 위상각이다. ψ의 값은 t=0에서의 F(t) 값에 의존하며 보통 0이다.
8.3.2 운동방정식 (Equation of Motion)
만약 힘 F(t)가 그림 8-28에서 보는 바와 같이 점성감쇠의 스프링-질량시스템에 가해진다면 운동방정식은 뉴튼의 제2법칙을 이용하여 구할 수 있다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (105)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (105)
이 방정식은 비동차이기 때문에 일반해 χ(t)는 동차해 ![]() 와 특수해
와 특수해 ![]() 의 합으로 주어진다. 동차해는 동차방정식
의 합으로 주어진다. 동차해는 동차방정식
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (106)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (106)
해이다. 식 (106)은 시스템의 자유진동을 나타내며 2항에서 언급되었다.
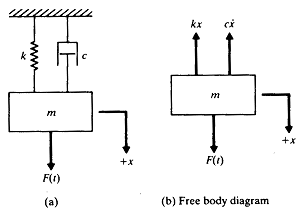
그림 8-28 스프링-질량-댐퍼시스템
2절에서 본바와 같이 자유진동은 3개의 가능한 감쇠조건과 모든 가능한 초기조건 하에서 시간이 경과함에 따라 소멸된다. 그러므로 식 (105)의 일반해는 결과적으로 특수해  와 같게되며 정상 상태를 나타낸다. 정상 상태의 운동은 강제함수가 존재하는 한 유지된다. 전형적인 경우에 대한 동차, 특수 및 일반해의 시간에 따른 변화가 그림 8-29에 제시되어 있다.
와 같게되며 정상 상태를 나타낸다. 정상 상태의 운동은 강제함수가 존재하는 한 유지된다. 전형적인 경우에 대한 동차, 특수 및 일반해의 시간에 따른 변화가 그림 8-29에 제시되어 있다.
![]() 는 소멸되고
는 소멸되고 ![]() 는 어떤 시간의 경과후
는 어떤 시간의 경과후 ![]() 가 됨을 볼 수 있다. 감쇠로 인해 소멸되는 운동의 일부분을 과도상태라 한다. 과도운동이 소멸되는 비율은 시스템의 변수
가 됨을 볼 수 있다. 감쇠로 인해 소멸되는 운동의 일부분을 과도상태라 한다. 과도운동이 소멸되는 비율은 시스템의 변수 ![]() , c 및 m 의 값에 좌우된다. 이 절에서는 과도상태는 생략하고 특수해만 유도한다.
, c 및 m 의 값에 좌우된다. 이 절에서는 과도상태는 생략하고 특수해만 유도한다.
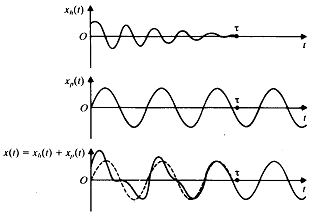
그림 8-29 부족감쇠에 대한 동차, 특수 및 일반해
8.3.3 조화가진에 대한 감쇠 시스템의 응답 (Response of a Damped System under Harmonic Force)
외력함수가 ![]() 로 주어지면 운동 방정식은
로 주어지면 운동 방정식은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (107)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (107)
식 (107)의 특수해는 역시 조화적이라고 예상되며 다음과 같은 형태를 가진다고 가정한다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (108)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (108)
Χ와 ψ는 결정되어야 할 상수이며, 각각 응답의 진폭과 위상각을 나타낸다.
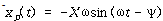
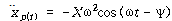
식 (108) 및 ![]() 식 (107)에 대입하면
식 (107)에 대입하면
![]() – – – – – – – – – – – – – – – – – (109)
– – – – – – – – – – – – – – – – – (109)
삼각법의 관계식을 이용하여
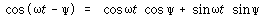
![]() – – – – – – – – – – – – – – – – – – – – – – – – – (110)
– – – – – – – – – – – – – – – – – – – – – – – – – (110)
가 되며 식 (109)를 위의 관계식을 이용하여 전개하면
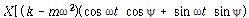
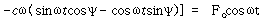
식 (110)을 cosω t 및 sinω t 항으로 정리하고 식 (109)와 비교하여 정리하면
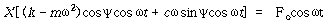
![]() – – – – – – – – – – – – – – – – – – – – – – – – – (111)
– – – – – – – – – – – – – – – – – – – – – – – – – (111)
이 된다. 앞에서 구한 2개의 방정식에 대해 cosωt나 sinωt의 상수항을 같다고 놓으면
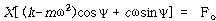
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (112)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (112)
행렬식으로 맞추기 위해 앞의 두 식을 순서가 맞도록 조정하면
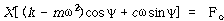
![]() 가 된다.
가 된다.
x 항을 정리하고 나면
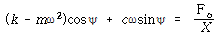
![]() 가 된다. 앞의 두 식을 행렬식으로 표현하면
가 된다. 앞의 두 식을 행렬식으로 표현하면
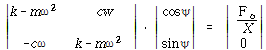 로 된다.
로 된다.
위의 행렬식을 풀면
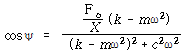
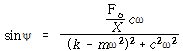 이 되고
이 되고
![]() 로부터
로부터
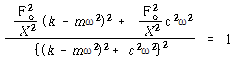
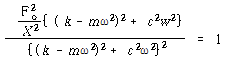
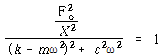
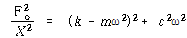
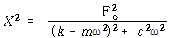
∴![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (113)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (113)
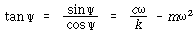
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (114)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (114)
식 (113)과 식 (114)을 식 (115)에 대입하면
![]() – – – – – – – – – – (115)
– – – – – – – – – – (115)
그림 8-30은 가진함수와 정상상태의 응답을 전형적인 그래프로 보여준다.
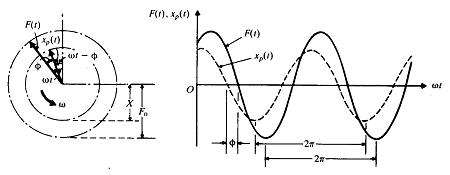
그림 8-30 가진함수와 그 응답의 그래프형태로 표현
식 (113)의 분모와 분리를![]() 로 나누고 다음 식을 대입하면
로 나누고 다음 식을 대입하면
![]() = 비감쇠 고유진동수
= 비감쇠 고유진동수
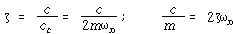
![]() = 가진력
= 가진력 ![]() 에 의한 정적변위
에 의한 정적변위
식 (113)을 변경하여
![]() = 주파수비로 나타내면
= 주파수비로 나타내면
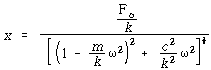
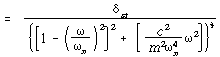
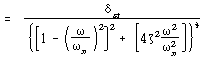
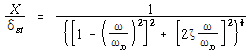
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (116)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (116)
가 된다. 같은 방법으로
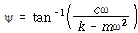
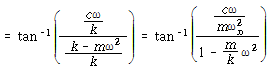
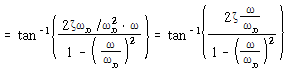
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (117)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (117)
![]() 는 확대계수(Magnification Factor), 증폭계수(Amplification Factor) 혹은 확대비라고 한다.
는 확대계수(Magnification Factor), 증폭계수(Amplification Factor) 혹은 확대비라고 한다. ![]() 및 ψ의 주파수비 r 및 감쇠비 ζ에 대한 변화가 그림 8-31에 나타나있다.
및 ψ의 주파수비 r 및 감쇠비 ζ에 대한 변화가 그림 8-31에 나타나있다.
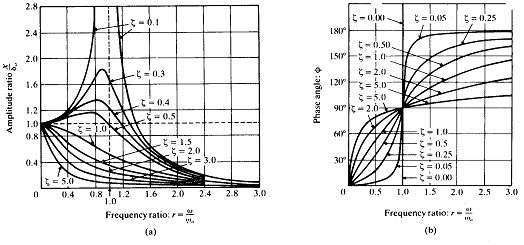
그림 8-31 주파수비 r에 따른 X 와 ψ의 변화
다음의 결과가 식 (116), 식 (117) 및 그림 8-31로부터 구해졌다.
① 부족감쇠계(ζ=0)에 대해 위상각 ψ=0가되고 식 (117)은
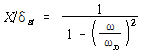 로 된다.
로 된다.
② 감쇠는 가진주파수의 모든 값에 대해 확대비를 감소시킨다.
③ 감쇠의 존재하에서 증폭비의 감소는 공진부근에서 매우 중요하다.
④ 감쇠가 존재하는 상태에서 최대 증폭비는 ![]() 혹은
혹은 ![]() 에서 나타나며 이는 비감쇠 고유진동수
에서 나타나며 이는 비감쇠 고유진동수![]() 과 감쇠 고유진동수
과 감쇠 고유진동수 ![]() 보다 더 낮은 주파수이다.
보다 더 낮은 주파수이다.
최대 확대비가 나타나는 주파수비를 찾기 위해서 식 (116)을 r에 대해 미분하고 좌변을 0으로 놓으면
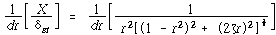
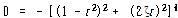
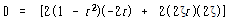
∴![]()
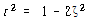
![]() (-항은 무시함)
(-항은 무시함)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (118)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (118)
가 된다.
⑤ X 의 최대값 (![]() 에서) 은
에서) 은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (119)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (119)
이다.
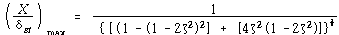
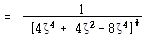
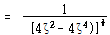
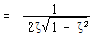
![]() 에서의 X값은
에서의 X값은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (120)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (120)
식 (119)은 시스템에 존재하는 감쇠 측정에 있어서 실험적 결정을 할 때에 사용할 수 있다. 진동 측정에 있어서 만약, 응답의 최대 진폭 ![]() 가 측정된다면 시스템의 감쇠비는 식 (119)을 사용함으로써 구할 수 있다. 역으로 만약 감쇠량을 알고 있다면 진동의 최대 진폭을 계산할 수 있다.
가 측정된다면 시스템의 감쇠비는 식 (119)을 사용함으로써 구할 수 있다. 역으로 만약 감쇠량을 알고 있다면 진동의 최대 진폭을 계산할 수 있다.
⑥![]() 에 대해 그림 8-31의 X 는 최대값이 없다. 그 이유는 식 (118)에서 ζ값이
에 대해 그림 8-31의 X 는 최대값이 없다. 그 이유는 식 (118)에서 ζ값이![]() 보다 큰 경우에는
보다 큰 경우에는 ![]() 가 허수가 되기 때문에 모든 값의 ω에 대해 최대값 혹은 피크값이 없다.
가 허수가 되기 때문에 모든 값의 ω에 대해 최대값 혹은 피크값이 없다.
감쇠가 감소함에 따라![]() 는 ω에 접근하며 일반적인 비감쇠 공진조건이 된다는 것을 주목해야 한다. ζ가 0에서 증가함에 따라 그림 8-31에서의 선도는 수직선 r=1에서 점점 더 왼쪽으로 떨어져서 피크를 가진다. 결국 감쇠비가
는 ω에 접근하며 일반적인 비감쇠 공진조건이 된다는 것을 주목해야 한다. ζ가 0에서 증가함에 따라 그림 8-31에서의 선도는 수직선 r=1에서 점점 더 왼쪽으로 떨어져서 피크를 가진다. 결국 감쇠비가 ![]() 보다 커지면
보다 커지면 ![]() 의 최대값은
의 최대값은 ![]() 에서 일어난다. 많은 경우에 ζ는 작으므로
에서 일어난다. 많은 경우에 ζ는 작으므로 ![]() 값은 1에 매우 가깝게 된다. 따라서 비감쇠 공진조건
값은 1에 매우 가깝게 된다. 따라서 비감쇠 공진조건 ![]() (즉,
(즉, ![]() )이 부족감쇠인 경우에도 공진에 대해 종종 사용된다. 예를 들면 ζ=0.1에 대해 비감쇠 고유진동수가 200 ㎐인 어떤 시스템은 198 ㎐의 피크값을 가지며 이것은 1%의 오차 보다 작다(
)이 부족감쇠인 경우에도 공진에 대해 종종 사용된다. 예를 들면 ζ=0.1에 대해 비감쇠 고유진동수가 200 ㎐인 어떤 시스템은 198 ㎐의 피크값을 가지며 이것은 1%의 오차 보다 작다(![]() 대신
대신 ![]() ). 따라서, 피크에 해당하는 주파수 값을 종종 단순히 고유진동수로 취할 때가 있다.
). 따라서, 피크에 해당하는 주파수 값을 종종 단순히 고유진동수로 취할 때가 있다.
⑦ 위상각은 시스템의 변수 m , c 및 ![]() 가 외력 주파수 ω에 따라 좌우되나 외력함수의 진폭 Fo와는 무관하다.
가 외력 주파수 ω에 따라 좌우되나 외력함수의 진폭 Fo와는 무관하다.
⑧ 응답 ![]() (t) 혹은 X가 외력함수 F(t) 혹은 Fo에 대해 지연되어 나타나는 위상각 ψ는
(t) 혹은 X가 외력함수 F(t) 혹은 Fo에 대해 지연되어 나타나는 위상각 ψ는 ![]() 의 값이 작을 때는 대단히 적다.
의 값이 작을 때는 대단히 적다.
![]() 의 값이 상당히 클 때는 위상각은 점차로 180˚에 접근한다. 그러므로 진동 진폭은
의 값이 상당히 클 때는 위상각은 점차로 180˚에 접근한다. 그러므로 진동 진폭은 ![]() <<1일 때 가진력에 대해 동위상(in-phase)이고
<<1일 때 가진력에 대해 동위상(in-phase)이고 ![]() >>1일 때는 역위상(Out of Phase)이다. 공진에서의 위상각은 모든 감쇠치에 대해 90˚이다.
>>1일 때는 역위상(Out of Phase)이다. 공진에서의 위상각은 모든 감쇠치에 대해 90˚이다.
⑨ 공진이하![]() 에서는 위상각은 감쇠가 증가함에 따라 증가한다.
에서는 위상각은 감쇠가 증가함에 따라 증가한다.
공진이상![]() 에서는 위상각은 감쇠가 증가함에 따라 감소한다.
에서는 위상각은 감쇠가 증가함에 따라 감소한다.
공진과 관련한 또 하나의 중요한 현상은 가진력과 이로 인한 진동간의 위상 관계(위상각)의 변화이다. 공진 주파수 이하에서 탁월한 구속력은 강성임이 분명하다. 환언하면 강성은 진동에 대항하는 주요한 힘이다. 그 결과 공진주파수 이하에서 발생하는 진동에 대해서는 강성력이 실제 진동 운동과 180˚ 위상차가 있음을 가정할 수 있다. 그러나 공진주파수 이상의 높은 주파수에서는 관성이 탁월한 구속력이 됨이 분명하다. 따라서 공진주파수 이상에서 발생하는 진동에 대해서는 관성력은 진동 운동과 180˚ 위상차가 있어야 한다. 그리고 그 결과는 시스템이 공진을 통과할 때나 그 시스템이 강성에 의해 주로 제어되는 상태로부터 관성에 의해 주로 제어되는 상태로 변화할 때 가진력과 실제 진동간의 위상각 관계에서 180˚ 변화가 있음이 틀림없다. 환언하면 공진 이하의 주파수에서 발생하는 진동에서는 기계의 진동 운동은 가진력과 동상이고 공진주파수 이상에서 발생하는 진동주파수에서는 기계의 진동 운동은 가진력과 역상(180˚ 위상차)이다.
그림 8-31은 고저 감쇠 시스템에서 진동주파수 함수로써 위상 관계의 변화를 나타내고 있다. 상당히 낮은 감쇠 시스템에서 180˚ 위상 변화는 대단히 작은 주파수 범위에서 발생할 수 있음을 기억하라. 또한 그림 8-31에서 정확히 공진 주파수에서 발생하는 위상 변화는 90˚임을 알 수 있다.
가진력과 이로 인한 진동 운동간의 위상 관계의 이러한 변화의 중요성은 축이 공진점, 그 이하 및 그 이상에서 운전할 때 불평형, 축진동 및 처짐의 영향을 나타내는 그림에서 잘 보여주고 있다. 임계 속도 이하의 속도에서 운전할 때 축은 주로 강성에 의해 제어되며 불평형력에 의해서는 상당히 작은 굽힘을 나타낸다. 실제로 임계속도 이하에서 운전할 때 축은 강성 로터로 간주된다. 그러나 임계속도 이상에서 운전할 때는 관성이 주요한 제어력이 되며 강성은 거의 관련이 없다. 그리고 로터의 임계속도 이상에서 운전할 때 근본적으로 강성이 없기 때문에 축은 탄성 상태가 되며 실제로 탄성 로터라고 한다. 이러한 상태 하에서 축은 저항이 가장 적은 길을 따른다. 즉 모든 축은 로터의 무게(또는 모멘트)가 균등하게 분포된 축인, 주관성축(Central Principal Axis)이라고 하는 축에 대하여 회전하려고 한다. 그리고 그림 8-32의 로터 무게는 무게 중심에 대하여 균등하게 분포되었고 또한 불평형은 축의 회전 중심으로부터 떨어져 무게 중심에 위치하고 있기 때문에 로터는 탄성에 의해 즉 강성이 없어 휘어질 것이고 따라서 회전축 즉 주관성축은 실제로 무게 중심을 통하여 통과한다. 이런 일이 발생하면 그림 8-32에서 로터 축은 실제로 Heavy Spot로부터 떨어져 휘게됨을 볼 수 있다. 환언하면 임계속도 이상에서 탄성 로터로써 운전할 때 축은 Heavy Spot과 180˚ 반대 방향으로 휠 것이다.
앞서 언급한 위상 문제는 학술적인 것 같이 보일지 모르지만 공진의 이해와 가진력과 그로 인한 진동 운동간에 존재하는 위상 관계에 미치는 공진의 영향이 공진을 정확히 진단하고 공진 문제를 해결하는데 아주 중요한 것임이 분명하다.
그림 8-32의 임계속도 이하에서 운전할 때 로터는 강성 상태가 되고 Unbalance Heavy Spot 쪽으로 휠 것이고, 임계속도 이상에서 운전할 때 로터는 탄성 상태가 되고 주관성축을 따라 회전하려고 할 것이며 Heavy Spot과 반대방향으로 휘게 하려는 힘이 작용한다.
⑩ 총 응답(Total Response)
완전해 ![]() 는
는
![]() – – – – – – – – – – – – – – – – – (121)
– – – – – – – – – – – – – – – – – (121)
여기서 ![]()
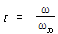

그림 8-32 임계속도 전후의 Unbalance 위치에 따른 로터 응답
8.3.4 회전 불평형에 대한 감쇠 시스템의 응답 (Response of a Damped System under Rotating Unbalance)
회전기계의 불평형은 진동의 주요 원인중의 하나이다. 이와 같은 기계의 단순모델이 그림 8-33에 나타나있다.
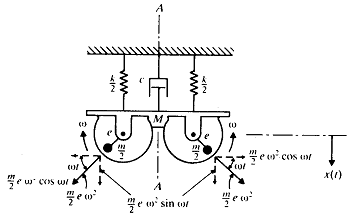
그림 8-33 회전 불평형 질량
이 기계의 총질량은 M이고 2개의 편심질량 m /2이 일정 각속도 ω로 서로 반대방향으로 회전하고 있다. 각 질량으로 인한 원심력 ![]() 는 질량 M을 가진 시키는 원인이 된다. 2개의 동등 질량 m /2이 서로 반대 방향으로 회전하게 함으로써 두 질량의 원심력의 수평방향 분력은 서로 상쇄된다. 그러나, 원심력의 수직분력은 서로 합해진다. 만약 질량의 각도의 시작점이 수평 위치로부터 시작한다면 원심력의 총 수직 분력은
는 질량 M을 가진 시키는 원인이 된다. 2개의 동등 질량 m /2이 서로 반대 방향으로 회전하게 함으로써 두 질량의 원심력의 수평방향 분력은 서로 상쇄된다. 그러나, 원심력의 수직분력은 서로 합해진다. 만약 질량의 각도의 시작점이 수평 위치로부터 시작한다면 원심력의 총 수직 분력은 ![]() 가 된다.
가 된다.
운동방정식은 다음과 같이 유도된다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (122)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (122)
이 방정식의 해는
![]() – – – – – – – – – – – – – – – – – – – – – – (123)
– – – – – – – – – – – – – – – – – – – – – – (123)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (124)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (124)
![]() 이라 하면
이라 하면
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (125)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (125)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (126)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (126)
각각의 ζ값에 대한 MΧ/ m e의 r에 대한 변화는 그림 8-34에 나타나 있다.
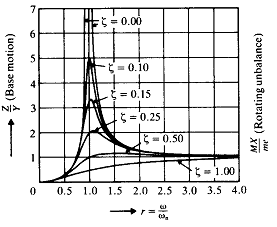
그림 8-34 주파수비 r에 대한 ![]()
다음의 결과는 식 (125)와 그림 8-33으로부터 구해진 것이다.
① 모든 곡선이 0의 진폭으로부터 시작한다. 공진 부근의 진폭![]() 은 감쇠에 의해 현저하게 영향을 받는다. 그래서 만약 기계가 공진부근에서 운전된다면 감쇠는 위험한 크기의 진폭을 피하기 위해 충분히 고려되어야만 한다.
은 감쇠에 의해 현저하게 영향을 받는다. 그래서 만약 기계가 공진부근에서 운전된다면 감쇠는 위험한 크기의 진폭을 피하기 위해 충분히 고려되어야만 한다.
② 아주 높은 속도에서는![]() 는 거의 1이 되고 감쇠 효과는 거의 무시된다.
는 거의 1이 되고 감쇠 효과는 거의 무시된다.
③ ![]() 의 최대값은
의 최대값은 ![]()
![]() 일 때이며
일 때이며
이 r값은 항상 1보다 크다.
피크 값은 공진에서의 값 (r>1)의 오른쪽에 나타난다.
[예제] 어떤 변속 전동기가 고정자와 회전자 사이의 반경 방향 간극이 1 ㎜이며 회전자의 질량은 25 ㎏이고 5 ㎏-㎜의 불평형량을 갖고 있다. 회전자는 그 베어링 사이의 중간에서 축위에 설치되어 있다. 두 베어링 사이의 거리는 2 m 이다. 이 기계의 운전속도는 600 rpm으로부터 6000 rpm까지 변화한다. 주어진 운전속도 범위내에서 로터는 항상 고정자와 접촉하지 않도록 하는 축의 직경을 결정하라. 감쇠는 무시한다.
[해]
회전 불평형으로 인한 축의 최대 진폭은
![]() (127)
(127)
로부터 구해진다. 여기서 me = 5 ㎏-㎜, M = 25 ㎏, X 의 제한값은 = 1 ㎜이다.
ω = 600 rpm일 때
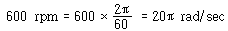
ω = 6000 rpm일 때
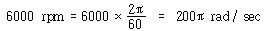
시스템의 고유진동수는 k 의 단위가 N/m라면
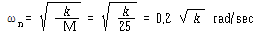
ω = 20π rad/sec에 대해
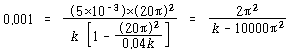
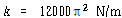
ω = 200π rad/sec에 대해
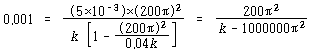
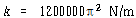
![]() 이 되도록 축을 제작함으로써 회전축의 진동진폭을 최소화할 수 있다. 그러므로, ω에 비해
이 되도록 축을 제작함으로써 회전축의 진동진폭을 최소화할 수 있다. 그러므로, ω에 비해![]() 이 작도록 해야하며, 그러기 위해서는 k 도 작아야만 한다. k 를
이 작도록 해야하며, 그러기 위해서는 k 도 작아야만 한다. k 를![]() 을 선택함으로써 앞에서 언급한 사항들을 만족할 수 있음을 알게된다. 중앙부하를 단순히 지지하고 있는 보의 강성은
을 선택함으로써 앞에서 언급한 사항들을 만족할 수 있음을 알게된다. 중앙부하를 단순히 지지하고 있는 보의 강성은