Data Formats and Methods for Vibration Analysis
1. 정적 및 동적 측정치 (Static and Dynamic Measurements)
2. 동적 신호의 표시방법 (Methods of Displaying Dynamic Signals)
3. 정상 상태의 자료형식 (Steady State Data Formats)
4. 과도상태 진동응답의 자료형식 (Transient Response Data Formats)
6. Shaft Orbit 분석 (Lissajous Pattern Analysis)
7. 모드/변형 형상 분석 (Mode/Deflection Shape Analysis
8. 위상 분석 (Phase Angle Analysis)
9. Full Spectrum 분석 (Full Spectrum Analysis)
1. 정적 및 동적 측정치 (Static and Dynamic Measurements)
기계 분석에 이용되는 측정치에는 정적 측정치와 동적 측정치의 두 가지 형식이 있다. Scaler 혹은 정적 측정치는 DC Type 측정치인데, 이는 측정된 변수를 하나의 특성 혹은 값으로 나타낼 수 있으며, 전형적으로 그 변화는 상대적으로 완만하게 발생한다. 정적 측정치에는 온도, 반경 및 축방향 위치, 부하 및 축 회전 속도 등이 있다.
동적 측정치는 AC 측정치인데 변수는 기계의 경우 거의 항상 주기적이다. 앞에서 설명한 것처럼 동적 신호는 3가지 특성 즉 진폭, 주파수 및 이미 알고 있는 기준에 대한 위상 관계로 나타낼 수 있다. 회전 기계에서 발생된 동적 신호는 일반적으로 회전 시스템 혹은 부품의 동역학과 관련되며, 한 사이클이나 그 이내에서 급속히 변할 수 있다. 소음은 가장 잘 알려진 동적 변수이다. 그렇지만 진동이 기계 상태 감시 및 진단에 훨씬 더 널리 사용된다. 소음보다 진동이 훨씬 더 널리 사용되는 몇 가지 이유가 있다. 발생원으로부터 감지기까지의 통로가 더 직접적이어서 주위 환경의 영향을 덜 받으며, 소음은 소음원의 멀고 가까움에 영향을 받는데 비하여 진동은 측정점에서 상태를 보다 자세히 나타내준다. Dynamic Strain도 동적인 측정치이나 자주 사용되지는 않는다. 비록 Dynamic Strain이 진동보다 측정하기가 더 어렵지만 터빈이나 압축기 Blade의 응력을 직접 측정하는 가장 훌륭한 방법이다.
어떤 측정치는 정적 및 동적 성분을 모두 가지고 있을 수 있다. 예를 들어 축방향 위치(정적 측정)는 일반적으로 모든 연속 감시 시스템에서 사용하고 있다. 비록 대부분의 위치 감시기가 정적 성분만 나타내도록 설계되어있지만 축 방향으로 설치된 비접촉식 감지기로부터 나오는 신호는 동적 성분을 포함하고 있다. 즉 여기서 동적 성분은 축방향 진동인데 이는 문제 분석과 상태감시에 유효하게 이용할 수 있는 변수이다. 마찬가지로 비접촉식의 반경 방향 축 변위 측정용 변환기로부터 나오는 신호는 반경 방향 진동과 축의 위치에 각각 비례하는 동적 및 정적 성분을 모두 가지고 있다. 반경 방향 축진동은 기계의 상태를 나타내는 훌륭한 지시치인 반면에 반경 방향 축 중심선 측정은 베어링의 손상을 검출하는데 아주 값진 역할을 한다.
축 회전 속도는 정적 변수로 분류된다. 축 속도는 대부분 동적 즉 AC 신호로부터 측정되는 반면 축 속도 그 차체는 그 신호의 한 특성 즉 주파수이며 따라서 이것은 정적인 량이다.
기계의 예방 감시를 위해서는 현재 값을 경보 설정치와 계속 비교할 것이 요구된다. 변화에 대하여 빠르게 감응하기 위해서는 정적인 값을 비교할 필요가 있다. 그러므로 복잡한 동적 진동 신호는 정적인 값(예를 들면 전체 진폭)을 나타내도록 처리되어야 한다. 그후에야 정적인 값은 경보치와 비교될 수 있으며 여러 가지 표시 형식으로 나타내지며 시간에 따라 경향 분석된다.
전형적으로 정적 값 그 자체는 가장 좋은 표시 방법이다. 하나의 정적 값은 아날로그나 막대 그래프, 디지털 숫자의 표시, 또는 시간에 따른 값의 변화 즉 그래픽으로 나타낸 경향 표시 등을 나타낼 수 있으며 이들은 쉽게 이해할 수 있다. 전형적으로 재래식 관례가 주어진 과제를 수행하는데 친숙한 표시를 나타낸다. 예를 들면 많은 사람들은 숫자로 나타낸 표시보다 재래식 시계 표지판에서 시간 보는 것을 좋아한다. 마찬가지로 자동차 속도 표시에 숫자로 표시하는 것이 잘 받아들여지지 않는다. 대부분의 사람들은 시계형 속도계를 좋아한다. 기계 감시에서 대부분의 사람들은 진동 진폭을 Vertical Meter나 막대 그래프로 나타내는 것을 좋아한다. 움직이는 값은 눈으로 쉽게 평균화되며 또한 보통의 관측자는 한 진동 형태에 익숙하게 되고 변화가 발생하면 쉽게 변화를 감지하나 수치로 나타내면 같은 경우에 숫자를 기억하여야 한다.
경보 설정치를 나타낼 수 있는 기능을 가지며 진동 진폭을 막대 그래프로 나타내면 여러 가지 이점이 있다. 때문에 현대의 많은 감시 시스템에서 이것을 적용하고 있으며 관찰자는 현재값이 경보치에 접근하는 현상을 일견하여 볼 수 있다. 온도, 축 회전 속도(rpm), 위상각 등은 전통적으로 숫자로 나타낸다.
축방향 위치는 중심인 0점을 기준으로 양측으로의 움직임을 전통적으로 아날로그로 표시하여 왔다. 여기서 다시 말하면 이렇게 나타낸 것이 실제 움직임과 유사하므로 알아보기가 쉽다.
2. 동적 신호의 표시 방법 (Methods of Displaying Dynamic Signals)
2.1 全體 振幅 (Overall Amplitude)
진동과 같은 동적 신호를 나타내는 가장 간단한 방법은 AC를 그것과 동등한 DC로 변환하여 계측기나 막대 그래프 등으로 나타내는 것이다. 휴대용 진동 계측기와 대부분의 진동 감시기는 이런 형태로 작동한다. 실제로 전체 진동값을 계측기로부터 읽고 그 다음 기계 상태 평가를 위하여 허용 진동값과 비교한다. 전체 진동을 수동으로 기록하고 그래프로도 그릴 수 있다. 그러나 컴퓨터를 이용한 저장, 경향 기록 및 표시가 훨씬 효율적이다. 주의할 점은 다른 계측기로 측정을 실시할 경우 전체 진폭이 같기 위해서는 5장에서 언급한 AC-to-DC 변환 방법이 있으며 계측기 통과 대역은 같아야 한다.
2.2 振幅, 周波數 및 位相角 (Amplitude, Frequency and Phase)
진폭, 주파수 및 위상각을 나타내기 위하여 통상 세 가지 방법이 사용된다.
• 필터를 통과하거나 혹은 가공하지 않은 신호를 Cursor를 사용하여 진폭, 주기 및 위상을 직접 시간 영역에서 나타낼 수 있다.
• 값들은 계측기 내에서 계산되며 수치로 보여준다.
• 신호를 주파수 영역으로 변환시킬 수 있으며 수치적 값은 Cursor의 위치를 조정하여 읽는다.
기계 상태 감시 및 분석을 위하여 사용되는 많은 계측기들은 이상의 세 가지 모두를 나타낼 수 있다.
진폭은 Cursor 위치를 이동하여 특정 주파수의 진폭은 물론 전체 진동값을 수치로 읽을 수 있다.
대부분의 분석기는 대수 눈금과 선형 눈금으로 전환 가능할 뿐만 아니라 매우 낮은 수준의 성분을 보기 위하여 진폭 눈금 확대 기능까지 가지고 있기도 하다. 대수 눈금은 전체 신호를 보여줄 뿐만 아니라 높은 수준의 성분이 있는 스펙트럼에서 매우 작은 수준의 성분을 강조하여 나타내며 선형 눈금은 높은 진폭 성분을 강조하여 나타낸다.
주파수도 역시 Cursor 위치 이동으로 값을 알 수 있다. FFT 분석기에서 Cursor는 실제적으로 한 Line(Bin)의 중심으로부터 인접 Line의 중심으로 이동한다. 그러므로 주파수 측정은 실제로 전체 눈금범위를 Line수로 나눈 값만큼씩 증가하게 된다.
위상은 여러 가지 방법으로 측정될 수 있다. 모두 축에 고정된 위상 기준을 가지고 있어야 한다. Fiberoptic, Infrared, Proximity Probe, 혹은 Strobe Tach 등에 의하여 감지되는 일회전당 한 번 발생하는(Once-per-turn) 위상 기준 신호는 Tracking 혹은 FFT 분석기의 Trigger 입력으로 연결될 수 있다. 위상각 측정은 기준 Trigger와 동기 성분의 진동 신호의 Positive Peak까지의 각도 차이이다.
2.3 Operating Deflection Shape(ODS)
위상을 측정할 수 있는 분석기는 특정 주파수나 주파수들로 진동하는 구조물의 운전시 변형 상태(Operating Deflection Shape)를 그려낼 수 있다. ODS 분석은 Modal Analysis와 구별되는데 이는 Modal Analysis가 외부 가진을 채택하는데 비하여 ODS는 정상적인 운전 상태에서 발생된 힘에 의한 변위(진폭)를 측정한다.
분석기가 ODS 분석을 위하여 사용될 때 위상의 기준이 되는 Pick-up은 위상 기준 마크를 제공하는 축에 위치하여야 한다. 진동 기준을 사용할 때 분석기를 동작시키기 전에 신호를 필터링 하는 것이 필요할 수도 있다. 일단 기준이 설정되면 기계나 구조물을 망 모양으로 세분하여 여기에 진동 Pick-up을 위치시키고 각 위치에서 진폭과 위상각을 기록한다. 이 자료들로부터 Mode Shape를 나타내는 그림을 그릴 수 있다. 똑같은 방법이 Strobe가 부착된 분석기에서 수행될 수 있는데 이 경우 위상을 측정하기 위하여 회전축에 표시를 하여야 한다는 것이 다르다.
2.4 時間 領域 (Time Domain)
2.4.1 振幅-時間 (Amplitude-Time)
시간을 수평축에, 진폭을 수직축에 동적 신호를 표시하는 방법을 시간 영역(Time Domain)이라 하며, 기계상태 분석에 이용되는 대부분의 FFT 분석기는 시간 영역으로 진동 신호를 직접 보여줄 수 있는 Oscilloscope 기능을 가지고 있다. Oscilloscope 대신에 이러한 형식의 계기를 사용할 때, 한가지 주의해야 할 점은 필터와 Sampling Process에 의해서 우리에게 보여지는 신호가 변경되거나 왜곡될지도 모른다는 것을 알고 있어야 한다는 점이다. 예로 Oscilloscope에 명확하게 나타나는 고속 Beat와 고주파 충격들은 FFT 분석기의 시간 영역 상에는 조금도 나타나지 않는다.
시간 영역 표시는 기계상태 분석에 매우 유용하다. Shaft Orbit, 기어 이빨 또는 Rolling Element 베어링의 결함으로 인해 발생되는 순간적인 충격, 그리고 Crank와 피스톤 핀의 접촉시 발생되는 충격(Slap)과 왕복동 기계에서의 Valve 작동과 같이 축의 회전과 관련된 동적인 현상들은 모두 시간 영역 상에서 가장 잘 관찰된다. 가장 단순한 시간 영역 표시는 단일 신호에 대한 진폭 대 시간 파형이다 (그림 7-1). 기계상태 분석기는 일반적으로 진폭과 수평축 상의 임의의 두 점간의 시간차를 측정하기 위한 Cursor를 가지고 있다.
일반적으로 임의의 두 점간의 시간차를 가장 정확하게 측정하는 방법은 여러 Cycle 동안의 시간차를 측정하고 이것을 평균하여 한 Cycle 동안에 걸린 시간을 얻는 것이다. 일단 한 Cycle 동안에 걸린 시간이 얻어지면 주파수(반복율)는 쉽게 계산되거나 즉시 표시될 수 있을 것이다.
만일 신호 분석기에 축이 한 번 회전할 때마다 위상 기준 신호를 발생시켜 주는 Trigger를 연결하여 사용한다면 대부분의 파형에서 Trigger가 위상 기준 신호를 발생시키는 위치에 하나의 점이 표시될 것이다. 이러한 위상 기준Trigger는 위상 측정에 있어서 기준이 된다.
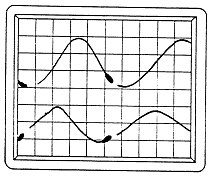
그림 7-1 단순한 시간 영역 파형
예로서 위상 기준과 High Spot 또는 특정점에서 측정된 순간 최대 진폭 사이의 각도차를 알아내기 위해서는 1 Cycle이 360˚라는 원리를 이용하여 두 점 사이의 각도 거리를 측정한다. 그림 7-2a는 축진동 변환기와 위상기준 변환기 (Keyphasor Transducer)가 동일한 수직면에 위치하고, High Spot 위치가 9시 방향에 있다. 로터상의 각도는 위상기준 마크인 Keyway가 0˚이고 로터 회전 반대 방향으로 각도가 증가하는 것으로 한다. 위상 측정은 Keyway가 위상 기준을 통과할 때(Keyphasor Pulse가 발생할 때)부터 로터의 최고 진동치 위치인 High Spot(Positive Peak)가 축진동 변환기로 검출될 때까지의 거리 또는 시간을 각도로 나타낸 것이다. 따라서 그림 7-2a의 경우는 High Spot 위치가 9시 방향에 있으므로 위상은 0˚ 위치인 Keyway 보다 90˚ 지연된 위치라고 한다.
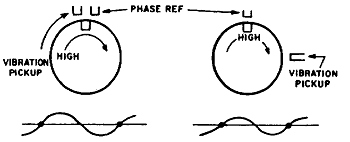
a b
그림 7-2 High Spot까지의 Phase Measurement
그림 7-2b는 축진동 변환기가 3시 방향으로 이동되었고 로터의 High Spot 위치는 0˚(12시 방향)인 경우로써 그림 7-2a와 마찬가지로 High Spot 각도는 90˚이다. 만일 그림 7-2a와 같이 High Spot이 9시 방향에 있다면 High Spot 각도는 180˚가 된다.
시간 영역 표시로부터 위상을 계산(Estimate)하여 Balancing에 이용할 수 있다. 더욱이 기계 분석시 장기간에 걸쳐 측정 위상이 변화한다는 것은 기계 상태의 판단에 값진 자료가 된다. 따라서 진동 경향을 알아보기 위해 진동 자료(특히 축진동)를 기록할 때는 필히 위상 측정치가 포함되어야 한다.
대부분의 컴퓨터화된 감시 및 분석 시스템은 위상 기준 입력이 주어지면 언제든지 자동으로 위상을 계산해 낸다. 이런 방법으로 위상은 다른 변수들처럼 직각 좌표계와 극좌표계에 표시할 수 있고 경향을 나타낼 수도 있다. 한가지 주의할 점은 2장의 내용을 상기해 볼 때 변위, 속도 그리고 가속도는 위상이 각각 90˚만큼 차이가 난다는 점이다. 그러므로 특정 계기에 따라서는 속도와 변위로 측정한 동일한 위상 측정이 90˚만큼 차이가 날것이다.
2.4.2 Orbit
대부분의 축변위 감시 시스템은 각 베어링에 원주 방향으로 90˚ 간격으로 설치된 2개의 변환기로부터 두 개의 신호를 만들어 낸다. 이 두 신호는 동시에 시간 영역 파형의 형태로 표시될 수 있다. 즉 두 신호가 하나의 Lissajous 즉 Orbit 표시 형태로 결합될 수 있다. Orbit 표시는 실제 축의 움직임을 크게 확대하여 이해하기 쉬운 매우 정밀한 그림을 보여주며 축의 움직임이나 응답을 분석하고 발란싱에도 이용될 수 있다.
진폭과 위상이 변화할 때 Shaft Orbit이 어떻게 응답하는가를 더 잘 이해하기 위해서 두 개의 파형을 손으로 작도하는 것이 교육적이다 (그림 7-3).
그림 7-3과 같이 참조 좌표상에 X 및 Y 파형을 상하로 구분하고 원점을 기준하여 오른쪽 및 위쪽을 각각 양으로 정한다. 축의 회전 증가분마다 Orbit을 만들기 위한 X 및 Y 파형의 조합을 위해 수치를 기록한다. 표 7-1은 그림 7-3의 파형에 기초하여 작성되었다.
X-Y 좌표의 동일한 번호에 해당하는 값을 조합하여 그래프를 그리면 그림 7-3의 오른쪽에 있는 Lissajou 즉 Orbital 형식을 얻게 된다. 그림 7-3에서 90˚의 위상차가 나며 진폭이 동일한 두 개의 순수한 정현파는 항상 원형 Orbit을 만들게 된다는 것을 알 수 있다. 기계상태 분석에 있어서 그림에 나타난 것과 같이 단순한 파형과 원형의 Orbit은 대칭 원통형 베어링에서 회전하고 있는 불평형 상태의 축에서 흔히 관찰된다. 만일 두 정현파의 진폭은 다르지만 위상차가 90˚라면 나타나는 Orbit은 최대 진폭 방향을 주축으로 하는 타원형일 것이다.
이러한 경우가 그림 7-3의 파형과 Orbit에서 점선으로 표시된 것이다. 타원형 Orbit은 중력이나 Pressure Dam 베어링 또는 Misalign된 상태의 축과 같이 외력이 축운동의 진폭을 한쪽 방향으로 억제하고 있는 기계의 상태를 분석할 때에 일반적으로 관찰된다.
그림 7-3의 예에서 진폭이 어떻게 변하든지 두 파형 사이의 위상차가 90˚를 유지하는 한 그로 인한 타원은 항상 X 및 Y 평면에서 정위치에 놓인 축을 가진다. 그림 7-4는 위상차가 90˚가 아니고 진폭도 서로 다른 두 개의 정현파에 의해서 만들어진 Orbit이다. 이 기울어진 타원형 Orbit은 150˚의 위상차를 가지고 있으며 진폭이 서로 다른 두 개의 정현파로 만들어진 것이다. 기울어진 타원형 Orbit은 일반적으로 Pressure Dam 베어링 또는 축의 Misalignment에 의해 발생되는 Preload의 결과로서 발생된다. 타원형 Orbit의 부축(Minor Axis) 은 축의 중심선과 Pressure Dam을 지나는 작용선(Line of Action)에 근접하게 될 것이고 또 축의 Misalignment의 방향을 지시할 것이다 (그림 7-5).
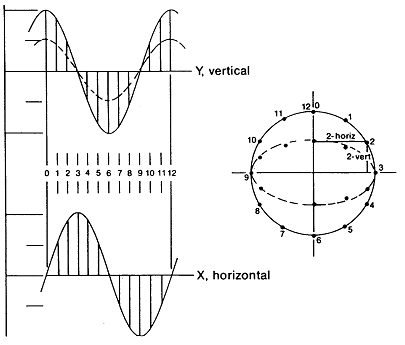
그림 7-3 90˚의 위상차를 갖는 두 정현파로 만들어진 Orbit

표 7-1 X-Y 진폭 성분, 위상은 90˚ 다름
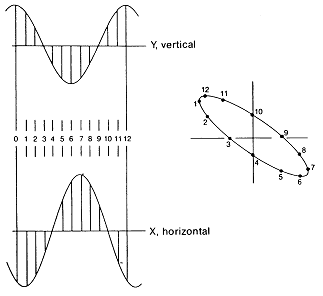
그림 7-4 위상차가 150˚이고 진폭이 다른 두 정현파형의 Orbit
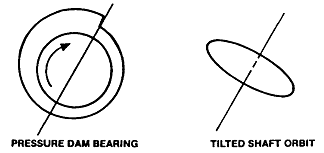
그림 7-5 압력 댐의 영향을 나타내는 기울어진 Orbit
만일 하나 이상의 주파수를 포함하고 있는 파형이라면 나타나는 Orbit은 포함된 주파수의 개수에 따라서 복잡해질 것이다. 그림 7-6은 기본파(기본 주파수)에 추가하여 기본파의 약 50% 정도의 차동기 성분을 포함하고 있는 두 개의 복잡한 파형으로부터 만들어진 Orbit의 유형이다. 불안정성과 관련하여 이런 형태의 파형과 Orbit은 부적절한 길이(L)/직경(D)를 가진 원통형의 유막저널 베어링을 사용하는 구형의 고속 기계에서 많이 관찰되었다.
앞서의 이러한 사항들에 대한 사전 지식을 가지고 다른 파형들에 대한 그래프를 작성해 보면 보다 기본적인 Orbit 형태들은 어떻게 만들어지는가에 대한 Idea가 떠오를 것이다. 그러나 축 변위 탐촉자로부터 얻어진 모든 신호들처럼 만일 그 신호에 축의 결함이나 또는 Runout의 영향이 포함되어 있다면 Orbit은 심하게 뒤틀려질 수 있고 또 유효성을 상실할 수도 있다.
게다가 만일 신호가 두 개 또는 세 개 이상의 주성분을 포함하고 있다면 나타나는 Orbit과 파형은 즉시 그 효용을 상실한다. 복잡한 Orbit의 경우에는 시간영역 표시에서 육안으로만 해석하기는 어렵다. 복잡한 신호를 단순화하기 위해서 Filtering 방법을 이용할 수 있으나 그럴 경우에는 중요한 Data가 손실되지 않도록 비상한 주의를 기울여야 한다 (그림 7-7). 대부분의 숙련된 분석가들은 모든 중요 데이터가 확실하게 수집되도록 운전 주파수에서와 1차 및 2차 차수에서의 보상되어진 Orbit과 함께 보상되지 않고 Filtering 되지 않은 Orbit도 함께 Printer로 출력할 것이다.
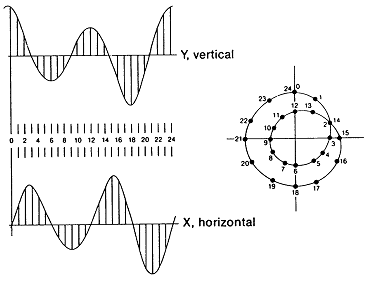
그림 7-6 축 불안정(Shaft Instability)을 나타내는 복잡한 Orbit
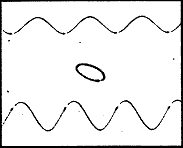

Bandpass filtered Unfiltered
to running frequency
그림 7-7 Filtered and Unfiltered 시간 영역 Signal
2.4.3 Smax
Shaft Orbit이 기울어져서 최대 진폭이 두 Probe 사이에서 발생했을 때(그림 7-8), 재래식의 X-Y 축변위 Monitor에서 얻어진 자료에 의한 진동 상태의 평가는 상당히 잘못된 것일 수 있다. 이러한 상황에서는 어떤 신호도 베어링 내에서의 상태를 전체적으로 나타내지 못한다. 이와 같은 상황에서는 실제 Orbit은 상당히 타원형인데 나타나기는 원형 또는 거의 원형에 가까운 Orbit의 형태로 나타날 수 있다. 이런 잘못될 가능성이 있는 상황을 없애기 위하여 최대 Peak-to-Peak 진폭이라고 정의된 계산된 값, 즉 Smax가 X 및 Y 신호값에 추가하여 또는 X 및 Y 신호값을 대신하여 진동상태 감시를 위하여 추천되어 왔다. Smax를 감시하면 축진동 진폭이 가장 높은 경우 또는 최악의 경우를 항상 알 수 있게 된다.
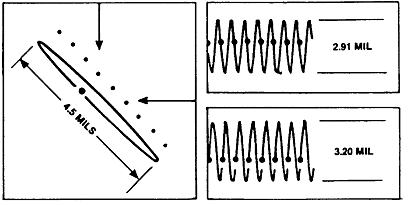
그림 7-8 터빈 발전기에서 측정된 시간 영역 파형(Time Waveform)과 기울어진 Orbit
2.5 周波數 領域 (Frequency Domain)
2.5.1 振幅 對 周波數 스펙트럼 (Amplitude Versus Frequency Spectra)
주파수 영역은 동적 신호를 나타내는 또 하나의 방법이며, 이의 좋은 예인 주파수 대 진폭 스펙트럼은 FFT 분석기나 Data Collector에서 쉽게 볼 수 있다(그림 7-9).
이런 종류의 표시는 진폭을 수직축에 표시하며 단위는 편리한 여러 가지를 사용한다. 수평축은 주파수 혹은 차수(회전 주파수의 배수)로 눈금 매김 되어 있다. FFT 스펙트럼 표시는 복잡한 진동 신호로부터 정보를 끌어내는데 유용한 수단이다. 신호의 주파수는 그 주기의 역에 비례하기 때문에 만약 진폭과 주기 혹은 주파수 중에 하나를 알면 한 영역으로부터 다른 영역으로 쉽게 변환될 수 있다. 그러므로 시간 혹은 주파수 영역에 미스터리는 없다. 간단히 말해서 이것들은 90˚ 각도를 이룬 두 개의 유리중 하나를 통하여 신호를 보는 것과 비교될 수 있다. 어떤 창이 좋은지는 측정 목적과 무엇을 조사하여야 하는 가에 달려있다.
스펙트럼 표시는 동적인 거동을 평가하기 위하여 실시간으로 나타낼 수 있다. 전산화된 감시 및 분석 시스템은 변화의 탐지와 분석을 위하여 저장된 스펙트럼을 다시 불러 볼 수가 있는데 이렇게 함으로써 보다 세밀한 분석이 가능하다. 많은 전산화된 시스템에서 저장된 스펙트럼을 자동적으로 정렬하고 찾아내며 또한 하나 혹은 그 이상의 여러 주파수 성분의 진동이 미리 설정한 값 이상 증가하면 경보를 하는 기능을 갖고 있다. 더 진보된 시스템은 단독의 이상 상태뿐만 아니라 통계적 이상 상태까지도 탐지할 수 있다.
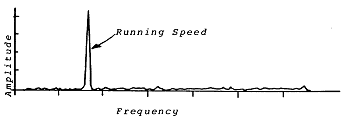
그림 7-9 FFT Display
2.5.2 制御할 수 있는 Cursor (Controllable Cursors)
제어할 수 있는 Cursor로 인하여 스펙트럼의 어느 위치에서나 진폭, 주파수, 위상(나타낼 수 있고 또한 입력이 위상 기준을 가지고 있을 때)을 빠르고 정확히 측정할 수 있다.
스펙트럼 표시에서 각 성분은 주파수를 축의 회전 주파수로 나누어 식별한다. 그 몫이 스펙트럼 성분의 배수 즉 조화차수(Harmonic Order) 이다. 낮은 차수-2배, 3배, 4배-는 통상 육안으로 식별된다. 더 높은 주파수에서는 분할을 하여 스펙트럼 성분의 차수를 구해야 한다. 일단 차수를 알면 그 성분은 흔히 그것을 발생시킬 수 있는 현상들과 관련시킬 수 있다. 이러한 예가 기어 맞물림 주파수(기어의 이빨 수에 축의 속도를 곱한 값)와 날개 통과 주파수(날개의 수에 축의 속도를 곱한 값)이다. 조화차수의 식별을 간단히 하기 위하여 대부분의 FFT 분석기는 Harmonic Cursor를 가지고 있다 (그림 7-10).
이 방법을 사용하면 주 Cursor가 위치한 주파수의 각 정수배에 Harmonic Cursor가 자동으로 위치한다. Harmonic Cursor는 복잡한 스펙트럼에서 날개 및 기어 맞물림 주파수와 같은 배수 성분을 식별하는데 아주 유용하다.
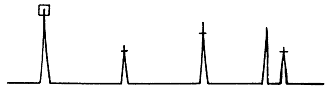
그림 7-10 Harmonic Cursor
대부분의 FFT 장비는 Difference Cursor 및 Sideband Cursor도 있다. Difference Cursor는 그 이름이 의미하는 바와 같이 표시 장치 상의 어떤 두 성분 사이의 주파수 차이를 직접 측정하는 것을 용이하게 해준다. 이의 특징은 합과 차의 주파수의 형태를 확인하는데 유용하다.
Sideband Cursor(그림 7-11)는 변조의 근원에 대한 진단시 신속한 확인을 위하여 중심 주파수의 양쪽에 일정한 간격을 유지하는 중심 주파수의 배수들을 표시한다. 이것은 Gear Mesh 주파수 근처 회전 주파수의 측대파와 전력 계통주파수의 두 배에 해당하는 주파수 근처에 있는 전동기 Slip 주파수의 측대파를 확인하는 용도로도 이용된다.
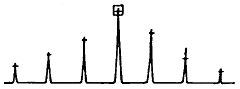
그림 7-11 Sideband Cursor
2.5.3 次數가 標準化된 Spectrum (Order Normalized Spectrum)
대부분의 FFT 분석기들은 위상 기준 입력 신호를 이용하여 차수 표준화 (Order Normalization)가 가능하다. 이러한 분석기 출력의 수직축은 진폭이며 수평축은 운전속도의 배수들이다 (그림 7-12). 차수가 표준화된 Spectrum에서 조화 성분들은 기계의 속도가 변하더라도 Display 상에서 그 위치가 일정하게 유지되는데 이러한 특징은 어떤 기간에 걸쳐 가변 속도형 기계의 특성을 비교하는데 아주 유리하다. 그러나 차수 표준화 표시방법이 불리할 때도 있다.
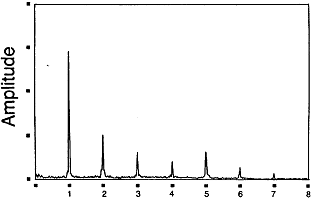
그림 7-12 Order Normalized Spectrum
Cascade Spectrum 항에 언급되어 있는 응답의 반전(Reversal of Response)은 종종 속도에 따른 진폭의 변화를 알아내기 어렵게 만든다. 예를 들면 공진은 실제로 특정 주파수에 고정되어 있는데 차수가 표준화된 화면에서는 움직이는 것처럼 나타난다. 회전속도 또는 그 배수가 되는 속도인 Exciting Frequency는 계속해서 변하지만 차수가 표준화된 표시 상에서는 고정되어 있는 것처럼 나타난다. 그러므로 차수가 표준화된 표시에서는 회전속도의 변화 또는 전달 통로를 따르는 Impedance의 변화에 의해 야기된 진폭 변화와 상태 변화 때문에 야기된 진폭 변화를 구별해 내는 어떤 손쉬운 시각화 방법이 없다. 진폭을 비교하는데 있어서는 Frequency Spectrum Plot 상에서의 진폭 비교가 약간 더 어려울는지 몰라도, 문제의 원인이 되는 주파수의 어떤 변화는 즉시 알 수 있게 된다.
2.5.4 Difference Spectra
Difference Spectrum (그림 7-13)은 정상상태를 나타내는 기준 즉 기본 스펙트럼(Reference or Baseline Spectrum)과 비교를 용이하게 하는 유용한 표시방법이다. Difference Spectrum은 동일한 주파수대의 비교하고자 하는 Spectrum의 진폭에서 기준 Spectrum의 진폭을 차감함으로 해서 만들어진다. 이런 절차를 통해서 기준 즉 기본 값을 초과하는 진폭은 Positive Peak로 나타나고, 기준과 비교하여 진폭이 더 낮을 경우에는 Negative Peak로 나타나며, 변화가 없는 경우에는 일직선으로 나타나는 Spectrum이 만들어진다. Difference Spectrum을 만들기 위해서는 동일한 속도 또는 동일한 차수 표준화 상태에서 기록된 Spectrum들이 필요하다.
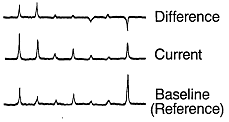
그림 7-13 Difference Spectrum
Difference Cascade (그림 7-14)는 일련의 Spectrum들, 특히 예측 감시를 위해 장기간에 걸쳐 기록된 Spectrum들을 비교하는데 매우 빠른 방법이다. 감시자는 단지 변화된 것만을 보게 되므로 현저한 특성에 주의를 빨리 기울일 수 있게 된다.
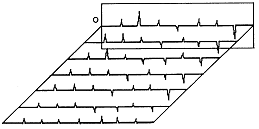
그림 7-14 Difference Cascade
3. 정상상태의 자료형식 (Steady State Data Formats)
3.1 傾向監視 (Trending)
기계의 정상 상태시의 감시는 장시간에 걸치거나 이와 관련된 상태 변화를 알아내기 위한 감시이다. 측정 결과를 시간의 함수로서 그래프화하는 경향감시는 사소한 변화라도 감지하는데 효과적인 방법이다. 사람의 눈과 뇌는 숫자표상에서는 전혀 감지해 내지 못할 것 같은 아주 작은 경향 변화를 감지해 낼 수 있는 강력한 컴비네이션을 이룬다. 경험에 의하면 진동 진폭의 변화율은 진폭이 높을 때보다도 낮을 때 훨씬 더 크다. 이것은 가장 초기의 경향 탐지 작업을 복잡하게 한다. 3~4회의 연속적인 측정을 통해 얻어진 적정한 곡선에 기초하여 경향 곡선을 만드는 것은 상태의 실제 변화를 반영하는 측정치 사이의 진폭 변화에 대한 확실성을 얻는 하나의 방법이다.
모든 현대의 컴퓨터화된 감시 시스템은 이력 정보에 기초한 경향을 나타낼 수 있는 기능을 가지고 있다. 대부분의 감시 시스템은 다음과 같은 사항에 대해서 하나 또는 그 이상을 인지하고 경보를 발생시켜 줄 것이다:
• 사용자가 정한 시간 간격 내에서 경보 설정치를 초과하는 값
• 미리 정해진 어떤 값을 초과하는 경향곡선(Trend Line)의 기울기 값
• 가장 최근의 값과 비교한 백분율 변화치
• 미리 설정된 표준 편차를 더하거나 뺀 계산된 값을 초과하는 현재의 값
이런 하나 또는 그 이상의 방법들을 이용하여 미세한 상승 발생시에도 실제로 경보 상황이 발생되기 훨씬 이전에 인지할 수 있다. 온도나 전체 진동값과 같은 정적 측정값을 경향 감시하는 것은 한 주파수에서 주된 증가가 발생했을 때 쉽게 이해된다. 신호가 더욱 복잡해질 때 그리고 신호가 수많은 성분들이 조합되어 만들어졌을 때는 전체 진동 경향은 그 신뢰도가 떨어진다. 한 개의 성분이 현저하게 변화해도 전체 신호 내에서는 간단히 관찰되지 않는다. 이러한 상황이 발생될 때는 특정 성분의 경향을 감시하기 위해서 예를 들어 회전 주파수와 같은 특정한 성분을 전체 신호로부터 분리할 수 있다. 다수의 Computer-Aided 감시 시스템은 복잡한 진동 신호를 진단 해석시 차동기 주파수, 운전 주파수, 운전 주파수의 2배 되는 주파수 등등과 같은 다수의 Band로 각각 분리할 수 있다. 적절하게 구성되기만 하면 이러한 유형의 경향은 다량의 정보를 알려줄 것이며 전체 진동의 경향에서 발견되어지는 것보다 훨씬 빨리 특정 성분의 변화를 감지할 것이다.
3.2 振輻, 位相 대 時間線圖 (The Amplitude, Phase Vs Time[APHT] Plot)
진동 진폭 및 위상각을 계속해서 기록하므로써 기계적인 문제가 시간의 경과에 따라 급격히 발생했는가, 점차적으로 발생했는가를 알 수 있다.
이것은 중요기계의 정지여부를 결정하는데 중요한 정보가 된다. 만약 진동이 오랜 기간에 걸쳐 매우 천천히 증가되어 왔다면 정비를 위한 정지는 필요시 연기할 수 있다. 그러나 만약 진동이 갑자기 증가했다면 상세분석과 정비를 즉시 실시해야 한다. 진폭위상대 시간은 기계적인 문제를 발견하는데 유용할 뿐 아니라 이상 상태를 진단하는데도 도움이 된다 (그림 7-15 참조).
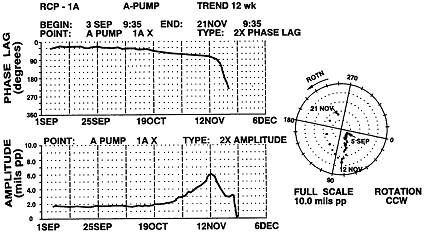
그림 7-15 n×의 진폭과 위상의 경향도
3.3 軸 中心線의 傾向 (The Shaft Centerline Trend)
X-Y Proximity Transducer로부터 DC Gap Voltage를 계속해서 감시해 두면 유용한 정보가 될 수 있다. 정상운전중, Slow Roll 중 및 정지중에 축 중심선의 위치변화는 기계의 힘이나 기계상태의 변화에 의한 것일 수 있다.
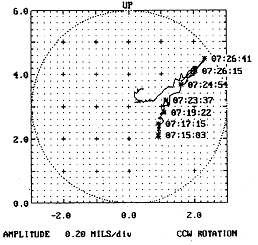
그림 7-16 Shaft Centerline Trend
3.4 Spectrum (周波數 대 振幅)
Spectrum은 진동주파수별 진동진폭 크기를 나타낸 것으로 Y축은 진폭, X축은 진동주파수를 나타내며 기계의 진동은 그 구성요소나 고장 원인에 따라 각기 고유한 주파수의 진동을 발생하므로 진동 발생원인 규명에 유효한 데이터이다 (그림 7-17).
진동 진폭 대 진동주파수는 여러 가지 방법으로 얻을 수 있는데 크게 나누어 Swept Filter를 이용하는 방법과 Real Time 분석기 (FFT)를 이용하는 방법이 있다. 수동 조정되는 간단한 Analyzer를 사용할 때는 Filter를 수동 조절하여 원하는 주파수에 맞추고 진폭과 주파수를 읽고 기록한다. 분석데이터를 수동으로 기록할 때 첫째로 Overall 즉 Filter-out 진동치와 진동이 가장 큰 주파수를 기록한다.
Filter-out 진폭과 주파수는 여러 가지 이유로 유용하다. 첫째, 진폭은 문제의 심각한 정도를 나타내며, Filter-in 진폭과 비교하여 주파수 분석이 완전하게 이루어졌는가를 알 수 있게 한다. 진동이 가장 큰 주파수는 문제의 근원이므로 이 주파수에 유의해야 한다. 그러나 문제점의 특성에 대한 결론은 Filter out 값만으로 기준으로 해서는 안되고 최종결정을 내리기 전에 철저한 진동주파수 분석이 이루어져야 한다.
필요한 Filter-in 측정치를 얻기 위해서는 조정필터로 각 주파수대를 주의하여 Scanning해야 한다. 각 주파수별 진폭을 측정한 후 측정이 잘되었는가를 즉시 점검하는 것이 좋다. 이것은 Filter-in 진폭과 Filter-out 진폭을 비교하므로써 알 수 있는데 일반적으로 Filter-in 진폭의 합계가 Filter-out 값보다 크거나 같아야 한다.
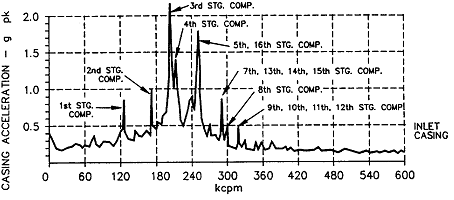
그림 7-17 Gas Turbine의 Blade Passing Frequency
3.5 Waterfall Plot (周波數 대 振幅 대 時間 = Spectrum 대 時間)
Waterfall Plot은 선택된 기계 진동 측정점에서의 스펙트럼들을 일정시간 주기로 나타내어 비교한 것이다. 가장 좋은 비교는 동일한 운전 조건하에서 스펙트럼을 취했을 때 이루어진다. Waterfall Plot은 진동 스펙트럼의 분명한 경향을 나타낸다. 기계응답의 변화를 분석하면 특정기계의 고장을 확인하는데 도움이 될 수 있다 (그림 7-18).
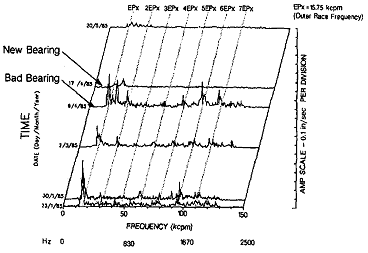
그림 7-18 Waterfall Plot
4. 과도상태 진동응답의 자료형식 (Transient Response Data Formats)
정상 상태의 자료들은 기계 상태의 경향을 분석하는데 유용하고 과도상태의 자료들은 정상상태의 자료에서는 얻을 수 없는 기동에서 정격 운전 속도까지 및 Coastdown과 같은 과도현상 동안의 기계 상태에 대한 지식을 제공한다. 베어링 안정성과 감쇠, 불평형 응답, 구조상 및 구성요소의 공진의 존재, 임계속도, 전자기적인 이상 상태, Rub와 축 균열 등은 과도상태의 자료를 가지고 가장 잘 탐지되고 분석되는 상태의 예이다. 과도상태 자료의 표시에는 3차원 즉 시간 또는 회전속도를 추가 포함하고 있어야 한다. 그러므로 과도상태 표시는 동등의 정상상태 표시보다 더 복잡하고 일회전마다 한번의 Pulse를 발생하는 기구를 필요로 한다.
4.1 Bode Plot (振幅/位相角 대 rpm)
회전기계의 응답특성을 나타내는데는 일반적으로 Bode Plot이 사용되는데 이는 rpm에 대한 진동진폭(1×)과 또한 rpm에 대한 진동진폭 Vector의 위상 지연각을 함께 나타낸 것이다 (그림 7-19 및 7-20).
Bode Plot에 담겨져 있는 정보를 통해 임계속도를 알아낼 수 있고 로터가 가지고 있는 감쇠를 평가할 수도 있으며 또 Balance 교정을 할 경우에 최적의 속도를 결정할 수 있다. 기계 상태 분석에 있어서 대부분의 Bode Plot은 축변위 변환기의 출력으로부터 작성된다. 여기서 주의할 점은 만일 축변위 변환기로부터 들어오는 신호에 조금이나마 감지할 수 있을 정도의 축 굽음이나 Runout에 대한 신호가 포함되어 있다면 Bode Plot은 왜곡되어질 것이다. Runout (즉, 축 거동과 관계없이 변환기 출력을 만들어 내는 측정대상인 축 표면의 어떤 기계적 또는 전기적 편차)과 축 굽음은 Bode Plot의 위상과 진폭 부분에서의 Initial Vector 또는 Offset을 야기할 것이다. 축 속도가 변할 때, 축의 굽음과 Runout 값(아마 일정한 값일 것임)은 변환기로부터의 총 출력신호를 발생시키는 실제 축의 움직임과 벡터적으로 결합한다. 이를 무보상(Uncompensated) Bode Plot이라 하며 Slow Roll 속도나 벡터를 구하는 경우를 제외하고는 사용되지 않는다(그림 7-19). 만일 축 굽음 또는 Runout이 전체 신호의 대부분이라면 이 신호는 Bode Plot의 모양을 크게 변화시킬 수 있다.
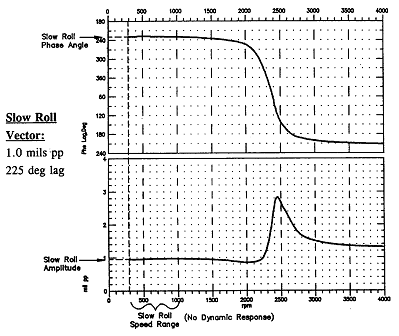
그림 7-19 무보상 Bode Plot
실재 임계 속도로부터 상당히 멀리 떨어진 진폭의 Peak값과 위상의 변화, 180˚ 내외에서의 위상의 변화, Peak가 발생하기보다는 진폭의 감소가 발생하는 경우 또는 아무런 응답이 없는 것 등은 심한 정도의 Runout이 있을 경우 발생할 수 있다. 그러므로 최대 운전속도의 약 5%에 해당하는 속도(Slow Roll 속도) 이하에서 “0”에 접근하지 않는 진폭 응답의 Bode Plot은 그 응답에 오차를 포함하고 있다. 이 오차를 제거하기 위해서는 Slow Roll 상태에서의 초기 Runout 성분(진폭 및 위상)을 벡터적으로 빼주어야 한다. 이를 보상된(Compensated) Bode Plot이라 한다 (그림 7-20). Bode Plot을 작성해 내는 계기들과 프로그램들은 Slow Roll의 보상과 Sampling한 각 속도에서의 자동 교정 기능을 가지고 있다.
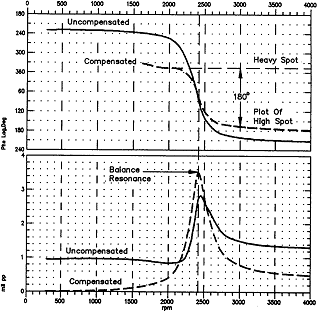
그림 7-20 보상된 Bode Plot
Bode Plot을 작도하는데 추천된 규칙은 다음과 같다.
① 위상지연각(Φ Lag) 대 rpm은 그래프의 상부에 그린다.
② 그래프에서 위상지연각의 증가방향이 아래가 되도록 그린다.
③ 그래프 아래에 1×(Absolute Rotative Speed Amplitude) 진동값을 그린다.
④ 완성된 위상지연각 곡선에서 High Spot-Heavy Spot 관계를 확인한다.
⑤ 각 공진속도 아래의 Rotor 회전속도에서의 1×(Rotative Speed Absolute Amplitude) 값을 무효화(Zero Nulling)시킨다. 이것을 무효화시키지 않으면 항상 잘못된 Plot이 그려진다. 오류가 없는 1× Bode Plot은 먼저 무효화 작업을 거쳐야 한다.
4.2 Polar(Nyquist) Plot (振幅 대 位相角 대 rpm)
Polar Plot은 극좌표에서 축의 회전속도 함수로써 그려진 일련의 진동 Vector(전형적으로 1×)이다. 각기 다른 회전속도에서 1×의 진동 Vector의 진폭 및 위상지연각은 2축상에 직접 그려지고 대응하는 축 회전속도도 기재되어 있다.
Polar Plot은 Bode Plot과 동일한 정보를 가지고 있으나, 강조하는 바는 다르다. 즉 Slow Roll Speed, Slow Roll Vector 및 동기 증폭계수는 통상 Bode Plot에서 얻기가 용이하고, Heavy Spot와 Structural Resonance는 통상 Polar Plot으로 확인하기가 보다 쉬우며 발란싱 목적으로 많이 사용된다.
Polar Plot은 좌표상에 표시되는 내용이 Bode Plot과 같지만 Bode Plot이 갖지 못한 몇 가지 이점을 갖고 있다. 첫째, Bode Plot처럼 따로 분리되어 표시된 진폭과 위상각을 비교할 필요없이 즉시 Unbalance Vector를 알 수 있다. 둘째, Bode Plot에서 진동진폭치가 작으면 위상각이 나타나지 않으나 Polar Plot에서는 나타난다. 셋째, 여러 베어링으로부터 구한 Polar Plot을 비교하여 쉽게 Mode Shape을 구할 수 있다. 근래에 들어 Polar Plot의 인기가 증가하여 점점 널리 사용되고 있는데 그 이유는 이상의 장점 이외에도 다음과 같은 특징이 있기 때문이다.
Bode Plot의 모양이 Runout이나 축 굽음(Bow)의 존재에 의해 심하게 변형될 수 있음에 반해, 그림 7-21 및 7-22에서와 같이 Polar Plot의 형태나 모양은 Runout이나 축 굽음과 관계가 없고 또 그로부터 영향을 받지 않는다. 그림 7-21에서 어떠한 축 굽음이나 Runout의 존재는 Slow Roll(Initial) Vector로 나타나며 이를 무보상 Polar Plot 이라 한다. 이러한 영향을 제거하기 위해서는, Plot의 원점(시작점)을 Initial Vector의 머리(끝)로 이동시켜야 한다. 새로운 원점을 기준으로 하여 원점 이후에 이어지는 어떤 벡터들도 벡터적인 차감이 자동적으로 적용되어, 무보상 Polar Plot에 대해 교정이 이루어진 것을 보상된 Polar Plot 이라 한다(그림 7-22).
또한 Polar Plot는 회전기계의 거동을 아주 분명하게 나타내준다. 예를 들면
① 각 Lateral Plane에서 Heavy Spot 대 High Spot이 전 속도범위에 걸쳐 관찰된다.
② 여러 개의 Lateral Plane을 이용하면 이것은 각 속도에서 축의 3차원 모양을 보여준다.
③ 위 그림에서 기계 발란싱을 위한 불평형 상태를 알 수 있다.
④ 고의적으로 불평형 상태를 만들어 그 응답을 관찰함으로서 기계적인 Impedance 일반특성을 관찰할 수도 있다.
⑤ Polar Plot은 Bode Plot과는 달리 축의 휨의 영향을 받지 않는다.
⑥ Polar Plot으로부터 각 공진 곡선(Loop)을 직접 측정하여 운동 증폭 계수를 알 수 있으며, 이로부터 감쇠율(Damping Factor)을 쉽게 구할 수 있다.
⑦ Polar Plot을 자세히 살펴보면 Heavy Spot과 High Spot을 알아낼 수 있다.
⑧ Piping, 커플링 Shroud, 기초 등의 공진과 같은 2차 공진은 Polar Plot에서는 Inner Loop로 나타나는데 이 경우 Bode Plot에서는 거의 구별하기가 어렵다.
⑨ 지지계의 Mismatch(Anisotropy)가 Polar Plot에서는 분명하게 나타난다.
⑩ Impedance가 가진의 함수로 변하며 응답크기가 Polar Plot에서는 분명하게 나타난다.
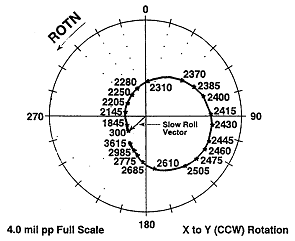
그림 7-21 무보상 Polar Plot
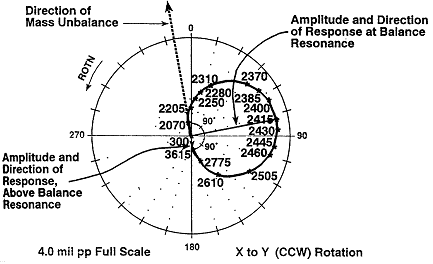
그림 7-22 보상된 Polar Plot
4.3 Cascade (周波數 대 振幅 대 rpm = Spectrum 대 rpm)
Bode와 Nyquist Plot은 본래 운전 주파수에서의 응답을 관찰하기 위하여 이용되었다. 그러나 꽤 자주, 속도가 변화하는 동안의 주파수 Spectrum 내의 몇몇 성분의 동적 거동을 관찰할 때도 유리하다. 이러한 상태하에서 Cascade Spectrum은 유용한 정보를 제공해 줄 수 있다.
Waterfall과 Cascade는 비슷하나 Waterfall이 Spectrum을 시간대별로 나타내 주는 것, 즉 Spectrum의 경향분석인데 비하여 Cascade는 Spectrum을 회전기의 속도별로 나타낸 것이다. 따라서 정상 운전상태일때는 Waterfall이 사용되며 과도 운전상태일때는 Cascade가 사용된다. 비록 과도상태일지라도 일정 회전수마다가 아닌 일정시간마다 Sampling하여 Waterfall을 사용할 수는 있다.
하나의 Spectrum은 특별한 속도, 특별한 부하에서 한순간의 진동 특성을 보여주는데 이것을 계속 반복하여 관찰하는 것이 필요한 경우가 많다. 예를 들어 기계의 기동시 기계의 각 부품에 의하여 발생된 여러 주파수에 의하여 임계속도에서 가진 되는지 혹은 공진구간이 있는지를 알아야 한다.
또한 부하, 온도 등 다른 운전변수의 변동에 따른 기계의 진동진폭과 주파수의 변화를 알아야 할 필요가 있을 수 있다. Real Time Spectrum Analyzer는 고속으로 분석할 수 있는 능력이 있기 때문에 이러한 요구조건에 이상적으로 부응할 수 있다. 즉, Cascade 및 Waterfall은 고유진동역의 통과여부, Oil Whip과 Oil Whirl의 존재 및 Oil Whirl로부터 Oil Whip으로 변화되는 모습은 물론 1×, 2×, 3× 등의 존재여부와 이들의 크기를 비교할 수 있으므로 진동원인 규명에 아주 유용하다 (그림 7-23 참조).
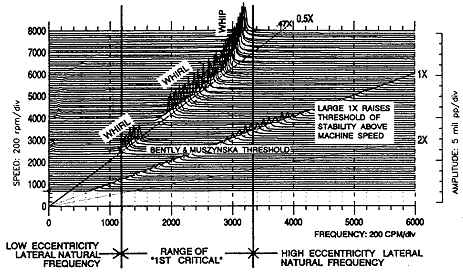
그림 7-23 Cascade Plot
5. 파형 분석 (Waveform Analysis)
비록 진폭 대 주파수(스펙트럼) 특성에 의한 진동분석이 기계 진동문제 해결에 유용하지만 때로는 특별한 운전조건에서 운전되는 기계의 결함을 진단하고 운동특성(Dynamic Behavior)을 연구하기 위한 또 다른 정보가 필요한데, 그림 7-24와 같이 오실로스코프에 나타나는 진동의 파형을 관찰하는 것이 도움이 된다. 파형의 수직축은 진폭이고 수평축은 시간을 나타낸다.
기계에서 발생하는 진동파형을 Oscilloscope에서 관찰하면 많은 기계의 문제점들을 확인할 수 있다. 예를 들면 불평형 및 Misalignment시 정상적인 파형은 그림 7-24a와 같이 정현파를 발생한다. 마찬가지로 기계적 이완, Oil Whirl 및 구름 베어링의 손상시는 그림 7-24 b, c, d와 같은 진동 파형이 생긴다. Oscilloscope의 또 다른 용도로는 충격 또는 과도상태 진동을 측정하는데 사용된다.
Scratch가 발생된 축의 진동 진폭과 주파수를 비접촉식 Pickup으로부터 측정하면 실제 축진동과 다른 값이 검출되므로 Oscilloscope에 연결하여 보면 Scratch의 특성이 Spike와 같은 신호로 나타나 쉽게 알 수 있다.
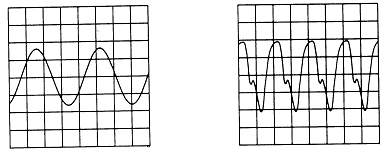
a) 불평형이나 Misalignment시의 파형(1×RPM) b) 기계적 이완시의 파형(2×RPM)
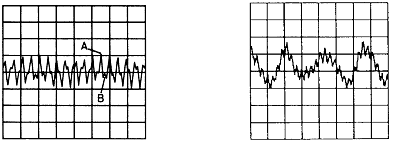
c) 작은 신호 “B”는 1×RPM 파형 d) 구름베어링 손상시 1×RPM에
“A”는 Oil Whirl 파형 고주파가 중첩된 파형
그림 7-24 전형적인 Time-Waveform
어떤 기계적 문제는 주파수는 같더라도 운동특성은 아주 다르다. 예를 들어 기어에서 하나의 이가 변형되거나 손상된 경우 그이는 매 회전시마다 맞물리는 기어에 충격을 가하여 1×RPM의 진동주파수를 발생할 것이다. 이것은 불평형에 의한 진동으로 잘못 판단할 수 있다.
그러나 파형으로 보면 손상된 기어에 의한 진동과 불평형에 의한 진동은 그림 7-25와 같이 확연히 구별된다. 불평형에 의한 진동은 정현 곡선 모양인 반면에 손상된 기어에 의한 진동은 못과 같은(Spike-Like)모양이다. 또한 손상된 기어 이빨에 의하여 실제 진동진폭이 나타날 수 있는가 하는 것도 의심스럽다. 못 모양의 신호는 주파수 분석을 위해 필터를 통과하면 진폭이 나타난다.

그림 7-25 불평형에 의한 진동과 손상된 기어에 의한 진동과의 파형 비교
진동의 파형을 관찰하는 또 다른 이점은 Oscilloscope에 의하여 감쇠되지 않은 진동모양을 즉시 볼 수 있다는 것이다. 따라서 짧은 과도상태 진동을 분석하는데 Oscilloscope는 아주 중요한 역할을 한다. 예를 들어 그림 7-26은 전동기의 기동시 얻은 과도상태 진동을 나타낸다. 이 진동은 아주 짧은 기간만 나타나지만 Oscilloscope에 실제 Peak 진폭이 쉽게 나타난다.
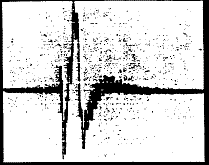
그림 7-26 전동기 기동순간 진동의 파형 분석
대부분의 진동계와 분석기에 있는 진폭 측정기의 경우는 지침의 흔들림을 방지하기 위하여 Damping이 있어 이 Damping 때문에 측정기의 응답이 늦어져 실제 Peak 진폭을 나타내지 못한다. 디지털 측정기라도 Reading값이 나타나기 전에 데이터를 “Count”해야하기 때문에 과도상태 진동의 실제 최대진폭을 나타내지 못한다.
6. 축 중심 궤적 분석 (Shaft Orbit [Lissajous Pattern] Analysis)
Spectrum 및 Waveform 이외에 진동해석에 유용한 데이터가 Shaft Orbit 이다. 이를 얻기 위해서는 각 베어링에 두개의 Non-Contact Pickup을 서로 90˚ 각도 떨어지게 설치해야 한다. 한 Pickup으로부터 발생된 신호는 Oscilloscope의 수평축 입력이 되고 다른 Pickup으로부터 발생된 출력은 수직축 입력이 된다. Pickup을 설치할 때 베어링 내에서 축의 수직방향 움직임이 Oscilloscope상에서 수직방향으로 나타나며, Oscilloscope 하단이 베어링의 하부로 나타나도록 계기를 Setup하는 것이 좋다. 그러나 Pickup을 정확히 수직과 수평방향으로 설치하기가 현장 작업상 어려운 경우는 45˚ 회전시켜 설치하는 경우가 많은데 이때는 Oscilloscope상에 Orbit가 45˚ 회전되어 나타나는 것 외에 다른 점은 없다.
최근에 Pickup 고장시 기계가 정지될 가능성을 줄이고 좀더 완전한 보호를 위해 중요한 고속 Turbo-Machine에는 보통 두개의 Non-Contact Pickup을 설치한다.
Oscilloscope상에서 Orbit을 관찰할 때 동기(1×RPM)와 같은 어떠한 주파수 기준이 없으면 주파수 정보를 얻을 수 없다. 예로써 그림 7-27과 같은 경우 주파수가 1×RPM인 경우에는 통상적으로 Unbalance 상태라고 간주될 수 있다. 그러나 만일 1×RPM 기준 Pulse가 그림 7-28과 같이 Orbit에 중첩 입력되면 그 해석은 완전히 다르다. 그림 7-28에서 동기 Pulse가 2번 나타나는데 축의 이러한 운동은 축이 2회전 할 때마다 한번 발생하는 것을 나타낸다. 따라서 이 진동은 분명 ½ 회전속도에서 발생하고 있다.
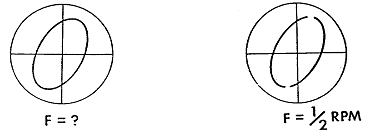
그림 7-27 주파수 정보가 없는 Orbit / 그림 7-28 축진동의 주파수 정보가 있는 1/2×RPM에서의 Orbit
동기 기준 Pulse는 Non-Contact Pickup(Proximity Probe)에 의해 얻을 수 있고, Oscilloscope가 장착되어 있으면 기준 Pulse를 “Z”축(Intensity) 입력단자로 보내면 Orbit상에 “Blank”점이 나타난다.
진동 원인별 Orbit 모양을 살펴보면 다음과 같다
6.1 Unbalance
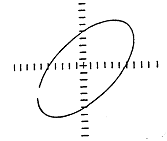
이상적으로는 순수한 불평형 상태의 Shaft Orbit은 완전한 진원이다 (그림 7-29(a)). 물론 원의 직경은 진동진폭의 증가에 따라 증가한다. 모든 실제 기계가 이상적인 조건에 아주 접근할지라도 불평형을 나타내는 Orbit의 모양은 타원이다 (그림 7-29(b)). 진원을 가지려면 베어링의 수평 및 수직 강성이 같아야 한다. 통상 기계는 수직방향으로 기초에 체결되기 때문에 수직방향의 강성이 더 크다. 중력의 영향 또한 수직 방향(하향방향)으로 작용하는 힘이다. 따라서 Orbit은 동일하지 않은 강성 즉 운동의 저항으로 인해 어느 정도의 타원이 된다.
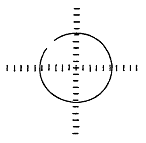
(a) (b)
그림 7-29 불평형 시의 전형적인 Orbit
Orbit이 어느 정도로 타원이 되어야 불평형 문제와 관계가 없을까? 엄격한 규칙은 없다. 일반적으로 Orbit의 큰 직경과 작은 직경의 비가 3:1 내지 5:1 정도면 아직도 불평형 상태에 있다고 할 수 있고, 그 비가 5:1을 초과하면 이 상태는 불평형보다는 Misalignment, 공진, 편심 또는 베어링 마멸에 의한 과도한 간극 등과 같은 다른 문제로 점차 기울어지는 것이다. 그러나 예외 없는 규칙은 없다라는 말을 명심할 것.
6.2 Misalignment
특히 커플링을 전후하여 축에 Misalignment가 존재하면 Orbit모양은 그림 7-30과 같은 심한 타원이 된다. 일반적으로 Misalignment 상태일 때 Orbit의 큰 직경과 작은 직경의 비는 3:1 내지 8:1이지만 통상은 5:1 내지 6:1이다. 그러나 불평형과는 달리 2×, 3× 또는 고조파 진동을 수반한다. 그림 7-31은 기계적 이완 문제 즉 축의 “End Play”의 영향이 결합된 Misalignment 상태의 Orbit이다. 이 타원은 변형 되였음에 주의하라. 완전한 8자 모양은 아니다. “꼬리”의 길이는 조화(변형)성분에 의한 상대적인 진폭 크기를 나타낸다. 만일 1×RPM 성분이 2×RPM 성분의 1 1/2 또는 2배의 진폭이면 그림 7-32와 같이 8자 모양을 띤다. 이 경우 역시, 전체 모양과 “꼬리”는 존재하는 다른 고조파 성분의 위상과 상대 진폭에 의하여 영향을 받는다.
Misalignment 상태가 과도한 경우는 다른 모양을 띨 수 있다. 즉 그림 7-33과 같은 Truncated Orbit, 그림 7-33(b)와 같은 Banana 모양의 Orbit및 그림 7-33(c)와 같은 복잡한 모양의 Orbit들이 있다. 이 복잡한 모양의 Orbit은 고조파 성분을 가지는 1×RPM 변위 성분의 변형에 의해 생긴다.
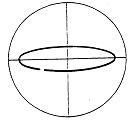
그림 7-30 Misalignment, 베어링 마멸 또는 공진시의 Orbit
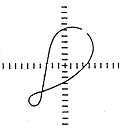
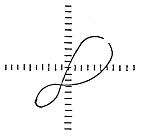
그림 7-31 Misalignment 및 기계 그림 7-32 1×RPM 비가 2:1인
이완 문제가 결합된 Orbit Misalignment 문제의 Orbit
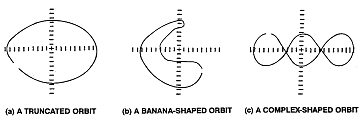
그림 7-33 과도한 Misalignment시의 Orbit
6.3 Orbit상에서 不平衡, 誤整列 또는 共振 區別
Orbit 분석만으로는 이런 문제들을 구별하는 확실한 방법이 없다. 한가지 해결 방법은 축속도를 더 높게 또는 더 낮게 변화시켜 보는 것이고 또 한가지 방법은 속도가 변화 할 때 기준 “Blank” Spot의 위치 변화를 관찰하는 것이다. 예를 들면 Orbit이 불평형 또는 공진에 의한 것인지를(특히 모양이 타원인지 아닌지를 ) 알아내기 위해서는 “Blank” Spot의 위치변화(방위측정)를 관찰하라. 만일 축이 1차 임계속도 아래에서 운전되고 축속도가 증가되었다면 Orbit상의 “Blank Spot는 바뀔 것이다. 공진시에는 “Blank” Spot는 축의 속도가 변화되기 전의 위치로부터 약 90˚ 바뀔 것이다. 축의 속도가 계속 증가하여 1차 임계속도를 지나면 “Blank” Spot는 원래 위치로부터 약 180˚ 바뀔 것이다. 그러나 이것은 축이 1차 임계속도 아래에서 운전되고 있다는 것을 가정한 것이다. 만일 축의 속도가 1차 및 2차 임계속도 사이에 있다면 “Blank” Spot의 변화가 1차 임계속도 아래의 속도에서 감소하는 것같이 유사하게 “Blank” Spot의 180˚ 위치변화가 관찰될 것이다. 이두가지 경우에서 타원 모양은 임계 속도에 가까이 있는 축의 속도에 기인한 것임이 결론지어진다. 이것은 불평형 상태에 기인한 것이 아니다. 만일 “Blank” Spot이 속도가 증가함에 따라 이동하지 않으면 문제점이 불평형이나 아마도 Misalignment로부터 기인한 것으로 결론 지을 수 있다.
타원 Orbit이 Misalignment 또는 공진으로 기인한 것인지를 알기 위해서는 속도가 변화했을 때 Orbit모양의 변화를 관찰하라. 축이 거의 임계속도에 가깝게 운전되고 있을 때 Orbit의 모양은 축의 속도가 증가되었는지 또는 감소되었는지에 따라서 상당히 변화한다. Orbit 직경의 대소의 비는 8:1 내지 10:1 이상이면 이것은 Rotor가 임계속도 가까이에서 또는 구조물 공진에 가까이에서 운전되고 있음을 강력히 암시한다. Orbit 모양에 영향을 미치는 축의 속도의 변화에 대하여 다시 한번 관찰하라.
이상의 내용은 지침을 의미하지 확실한 규칙은 아니다. 기계의 동적 거동은 대단히 복잡하다. 때로는 그 해는 이처럼 단순하지 않다. 예를 들면 많은 경우에 축의 속도를 증가시키거나 감소시키는 것이 쉬운 과정이 아니다.
6.4 Rotor Rubs
Rub는 일반적으로 로터가 베어링 표면이나 Seal과 같은 정지체와 접촉하므로써 발생되고 통상적인 원인은 과도한 불평형, Misalignment, Soft Foot, 과도한 베어링간극, 열적인 휨 등이 있다. Rotor Rub는 주로 부분 Rub와 전체 Rub로 구분하여 설명된다.
(1) 부분(약한) Rub
아주 약한 Rotor Rub는 축이 단지 1회전에 한번 정지체와 접촉하는 Rub이다. 이런 Rub의 결과는 그림 7-34와 같이 진원의 Orbit이 약간 변형되거나 타원이다. 약한 변형과 더불어 Orbit의 “Blank” Spot의 전후이동이 있다. Keyphasor Oscillation을 나타내는 “Blank” Spot의 이러한 이동이 특히 “Blank” Spot 의 위치가 10˚이상 변할 때 Keyphasor ”Jitter”라고 한다. 부분 Rub는 시간이 경과함에 따라 전체 Rub로 진전되기도 한다.
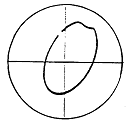
그림 7-34 아주 약한 Rub시의 Orbit
(2) 전체(심한) Rub
Rub가 더욱 심해지면 Orbit은 점차 더욱 복잡하고 일정하지 않는 경향을 띤다. 부품 공진이 가진될 수 있고, 고조파 주파수가 나타날 수 있으며 또한 비동기 주파수들은 상호작용하여 무한한 가능성 있는 영향을 생기게 한다. 그림 7-35는 전체 Rub시의 Orbit의 여러 가지 모양을 나타내는 예이다.
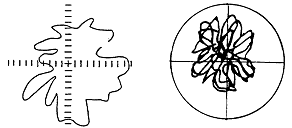
그림 7-35 전체 Rub시의 Orbit
“Blank” Spot의 Oscillation을 관찰하므로써 Rub의 정도를 알 수 있다. Rub로 인해 더 나쁜 상태로 될 때 “Blank” Spot 의 이동은 더욱 불규칙하고 일정하지 않게 된다. 이것은 Rub가 발생할 때 축에 발생하고 있는 것을 반영하는 것이다. 처음 약한 Rub가 발생하면 축 회전방향에 약한 저항이 있다. 상황이 더욱 나빠져 진폭의 크기가 증가하면 축회전 반대방향으로 베어링이나 Seal과 접촉하여 축상에 작용하는 접선력이 생긴다. 축이 실제로 정지체 표면과 접촉할 때에 Orbit에서 역세차 운동이 관찰될 것이다. 심한 Rub의 경우에서처럼 접선력이 커질 때 축은 회전하기 위해 구동되는 방향과 반대 방향으로 궤도를 그리며 돈다. 대부분의 경우 전체 Rub 상태로 운전하고 있는 축은 기계의 가공할 만한 손상을 초래한다. 그림 7-36은 심한 Rub시의 역세차 운동의 Orbit을 나타낸다.
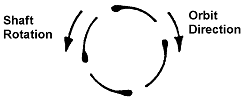
그림 7-36 전체 Rub시의 역세차 운동의 Orbit
(3) Hit and Bounce Rubs
약한 Rub와 심한 Rub 사이에 “Hit and Bounce”라고 하는 부분 Rub이 있다. Misalignment와 같은 상태는 축이 베어링 표면과 접촉하여 로터를 원주방향 바깥쪽으로 이동하게끔 억압할 수 있다. 그러나 상태가 악화됨에 따라 축은 충돌하고 튕겨 나오며 이로 인해 역세차 운동이 발생할 수 있다. 이것은 정확히 1/2×RPM에서 거의 발생하고 이때 Orbit은 Internal Loop를 가지게 된다. 상태가 더욱 악화됨에 따라 더 많은 충돌이 일어날수 있고, 그림 7-37에서와 같이 Orbit에 영향을 미친다. 충돌이 더욱 빈번할수록 Internal Loop는 더욱 촘촘해진다.
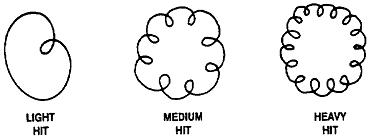
그림 7-37 여러 가지 Hit and Bounce Rub시의 Orbit들
(4) 결언
부분 Rub의 경우
•Internal Loop를 가지는 Orbit이 생긴다.
•“Blank” Spot가 Jitter한다.
전체 Rub의 경우
•Orbit회전은 축회전과 반대방향(역세차 운동)이다.
•Rub로 인해 축속도가 감소할지라도 주파수 및 역방향 Rub Orbit은 일정 하다.
6.5 Oil Whirl
Oil Whirl 은 통상 저널 베어링 및 가압 윤활 시스템을 가지는 기계에서 발생한다. 일반적으로 축은 길고 상당히 높은 회전수(1차 임계속도 이상)를 가진다. 불평형이나 Misalignment는 통상 Oil Whirl을 일으키는 힘을 공급하는 가진력을 준다.
축은 축을 들어올리는 영향을 가지는 Oil Wedge상에서 운전하려는 경향이 있다. 이 작은 불안정력은 축과 윤활유가 축회전 방향으로 강력하게 회전하도록 하는 가진력이 있어 축이 회전함에 따라 축을 Whirling하도록 한다. 이 Oil Whirl 주파수는 축 속도의 42~48%사이에 있다.
Oil Whirl 상태에서의 Orbit은 Displacement Orbit축에 대하여 서서히 회전하는 Internal Loop를 나타낸다. 이것은 회전과는 비동기이므로 Displacement Orbit과는 관계없는 주파수에서 회전한다. 그림 7-38은 Oil Whirl상태에 있는 축의 Orbit의 한 예이다.
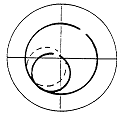
그림 7-38 Oil Whirl 상태에 있는 축의 Orbit 예
6.6 Mechanical Looseness
기계적인 이완에 의한 Orbit의 특성은 Rub의 경우와 유사하다. 기계적인 이완의 가장 일반적인 원인은 베어링의 간극이 너무 큰데 있다. 기계적인 이완의 현저한 결과는 1×RPM의 조화 진동뿐만 아니라 정수배의 차동기(통상 1/2× 또는 1/3×)진동이 있다는 것이다. 차동기 주파수는 Rotor Rub시의 Orbit과 유사한 Internal Loop를 생성한다. 물론 아주 복잡한 상황에서는 Orbit은 그림 7-39에서와 같이 매우 변화가 심하다.
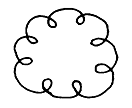
그림 7-39 기계적 이완에 의한 복잡한 Internal Loop를 나타내는 Orbit
6.7 Orbit상에서 機械的 弛緩, Rotor Rub 또는 Oil Whirl의 區別 方法
문제점이 기계적인 이완에 의한 것인지 Rotor Rub에 의한 것인지를 아는 주요 요점은 Orbit이 축의 회전과 관계하여 이동하는 방향을 아는데 있다. 만일 문제점이 기계적인 이완이라면 Orbit과 Internal Loop는 축이 회전하는 방향과 관계없이 고정된다. 만일 문제점이 Rotor Rub라면 Displacement Orbit은 특히 전체 Rub인 경우는 축회전과 반대 방향으로 회전하는 경향을 가진다.
문제가 기계적 이완으로부터 생긴 것인지 Oil Whirl로부터 생긴 것인지 알기 위해서는 Internal Loop를 참조할 것임. 만일 문제점이 Oil Whirl이라면 Internal Loop는 축의 회전방향과 같은 방향으로 천천히 회전한다. 만일 문제점이 기계적인 이완이라면 Loop는 1×RPM Displacement Orbit과 동기하고 있기 때문에 정지상태로 있다.
7. 모드/변형 형상 분석 (Mode/Deflection Shape Analysis)
질량이나 강성의 구조적 개선이 상당히 단순하고 올바르다 할지라도 추천하는 첫 번째 조치는 공진하는 시스템의 유한한 또는 특정한 부품을 확인하는 것이다. 이것은 Mode Shape 즉 Deflection Shape 분석을 하면 된다. 기계 및 지지 구조물의 Mode Shape 분석에는 여러 측정점에서 취한 진동진폭값과 진동 모양 및 공진 부품을 나타내기 위해 Chart상에 그려진 그림이 필요하다. 그림 7-40의 기계는 Bump Test, Coastdown Test 또는 다른 분석 기술에 의해 확인된 공진으로 수직 방향의 진동 진폭이 높다고 가정해 보자. 그림에서와 같이 구조물을 따라서 여러 위치에서 수직 방향의 진동 진폭을 단지 측정하고 기록함으로써 단순 Mode Shape을 취할 수 있다. 이 경우 측정점은 자료를 작도하기 위하여 동일 간격으로 위치되어야 한다. 자료를 작도하기 위하여 편리한 눈금을 사용하여 구조물의 그림을 그리고 각 측정점의 위치를 그림 상에 나타낸다. 그림 상의 각 측정점에서 측정한 진동 진폭과 동일한 길이로 수직선을 그린다. 그림 7-41에서 진폭 선은 어떠한 편리한 눈금을 사용해도 되지만 진동 진폭값의 범위에 기준하여 선정한다. 일단 모든 진폭선이 그려지면 그림 7-41과 같이 선의 끝부분을 연결한다. 취한 측정치가 진폭이 낮은 점 즉 절점이 있음을 나타내면 그림 7-41이 그림 9-37과 같이 Mode Shape가 생기는지의 여부를 알기 위하여 분명한 정점의 한쪽에서 측정한 진동에 대한 비교할 만한 위상값을 취할 필요가 있다.
그림 7-42의 Mode Shape 분석 결과 그 구조물이 정형파의 Mode 특성으로 인해 수직 방향으로 2차 탄성공진에서 진동하고 있음을 나타내고 있다. 공진 상태가 확인되었을 뿐만 아니라 절점도 잘 확인되고 있다. 수직 방향의 강성을 증가시킴으로써 구조물의 수직 방향공진을 변화시키려는 결정이 수립되어 그림 7-43과 같이 강성 보강재가 절점에 취부 된다면 어떠한 개선 결과도 얻기 못하기 때문에 Mode Shape 분석이 아주 중요하다. 가장 좋은 결과를 얻기 위해서는 최대 진폭 지점에 구조물이 보강되어야 하며 이 지점들은 Mode 분석에 의해 확실하게 확인된다.
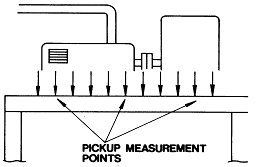
그림 7-40 구조물의 Mode Shape을 얻기 위하여 구조물을 따라서 균일한 간격을
가진 위치에서 진동 진폭과 위상을 측정한다.
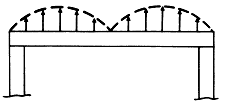
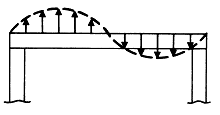
그림 7-41 Mode Shape를 작도하기 그림 7-42 진폭 값이 절점이 있음을
위하여 Chart 상에 각 위치에서의 나타내면 Mode Shape을 구하기
진동 진폭을 그린다. 위해서는 비교되는 위상 값이
필요하다.
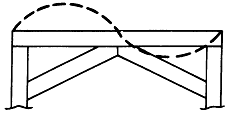
그림 7-43 절점에서의 구조물 강성 보강은 거의 개선이 되지 않는다.
Mode Shape 분석의 중요성을 설명하는 다른 사례로서 가스터빈으로 구동되는 발전기가 있다. 그림 7-44의 발전기는 주파수 3600 cpm 즉 1×RPM에서 수평방향으로 높은 진동(25.4 ㎜/sec)을 나타내었다. 수직 및 축방향 진동은 수평 방향 진동에 비하여 대단히 낮았기 때문에 수평 방향 공진이 예상되었다. Bump Test 결과 발전기는 3600 cpm에서 수평 방향의 고유 주파수를 가졌고 회전속도 주파수에서 공진 상태이었다. 모든 가능한 해결책을 강구한 후에 그림 7-44의 점선으로 나타난 바와 같이 철강 바침대로 용접하므로써 발전기의 강성을 높이려는 결정을 하였다. 받침대를 설치한 후 발전기를 기동하였으나 수평 방향의 진동은 전혀 개선되지 않았다. 그 결과 그림 7-45에서와 같은 Deflection Mode를 나타내는 다음 같은 Mode Shape 분석이 수행되었다. Mode Shape 분석 결과 강성 보강 개조는 시스템의 공진 부품 아래에 적용하여 공진 시스템을 강성 보강하는데는 전혀 효과가 없었음을 보여주고 있다.
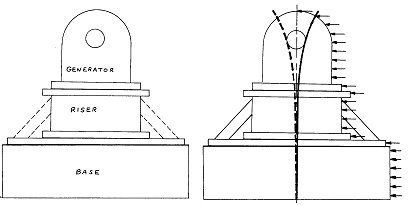
그림 7-44 수평 방향의 공진 주파수 그림 7-45 Mode Shape 분석결과
(1×RPM)에서 운전하는 이 발전기 발전기는 시스템의 공진 부품 아래
에는 진동개선에 전혀 개선이 안되도 보강되었음을 보여주고 있다.
록 강성 보강되었다.
그림 7-42~7-45에서 설명한 Mode Shape 분석은 2차원으로 나타낸 단순한 Mode Shape 만을 보여주고 있다. 그림 7-46에서와 같이 3차원의 기계 및 구조물의 Mode Shape 특성을 구하도록 이 분석 기술을 확장시킬 수 있다. 구조물을 모눈 모양으로 표시하고 표시된 각 위치에서의 진동 진폭과 위상각을 측정하고 기록한다. 기계 및 구조물의 3차원 도면 위에 이 값들을 그리고 시스템의 Mode를 나타내도록 진폭 Vector를 서로 연결한다.
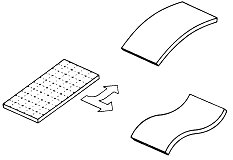
그림 7-46 3차원 그림으로 나타내도록 Mode Shape 분석 기술을 확장할 수 있다.
위 예에서 설명한바 와 같이 Mode Shape 분석은 좋은 결과를 얻기 위해 질량이나 강성의 구조적 개조가 행해져야 하는 것을 결정하는데는 가치가 있다. 이와 같은 분석을 행하지 않으면 전혀 개선되지 않을 수도 있다. 앞서 언급한 Mode Shape 분석 기술은 기본적인 진동 분석 계측기만이 필요한 단순한 것이다. 시스템의 진동 Mode Shape 특성의 자세한 설명이 필요하면 Software 회사로부터 Mode 분석 Computer Software를 구입하여 사용하면 된다. 먼저, 분석을 하고자하는 기계나 구조물의 개략도를 그려 진동 진폭과 위상각 측정이 취해질 곳을 확인한다. 자료를 취하고 Computer에 입력한 후 Software를 이용하여 진동 Mode의 움직이는 모습을 본다. 대부분의 Mode분석 Software Program은 운전 조작자가 상세한 검토를 하기 위하여 모든 위상각을 알아볼 수 있으며 동화상의 속도도 조정할 수 있도록 되어 있다.
Mode(Deflection) Shape 분석은 구조적인 개조에 앞서 공진 문제를 평가하는데 유용할 뿐만 아니라 구조물의 이완 및 취약과 같은 구조적인 문제를 확인하는데도 대단히 유용한 분석 기술이다.
8. 위상 분석 (Phase Angle Analysis)
위상각을 이용하면 로터의 발란싱, 축균열 검출, 축 또는 구조물의 공진 검출, 축의 Mode Shape, 진동의 방향 및 유체 유동에 의한 불안정 근원의 위치를 알아낼 수 있다.
8.1 로터 발란싱 (Rotor Balancing)
Balancing 이란 Heavy Spot의 량과 위치를 알아내어 이와 같은 량의 무게를 로터의 반대방향에 달거나 Heavy Spot에서 그만한 량을 제거하는 과정이다. 불평형량이 클수록 진동 진폭은 이에 비례하여 증가하며, 불평형의 위치를 알기 위해서는 Keyphasor Transducer나 Strobe Light를 이용한다. 이와 같이 로터의 질량불평형 상태를 교정하기 위해서는 불평형 위치 즉 위상각 측정 및 이용이 절대 필요하다. 보다 상세한 내용은 “Balancing” 항에서 언급할 것이다.
8.2 Cocked 베어링 또는 휜 축의 檢出 (Detecting of Cocked Bearing or Bent Shaft)
그림 7-47 및 7-48과 같은 축계에서 4곳(1, 2, 3, 4)의 베어링 하우징에서 축방향 위상각을 측정한 결과 모두가 동상(150˚)인 경우는 하우징이 Planner Motion을 하고 있는 경우이고, 각각 90˚ 차이를 가지는 경우는 (1과 3은 180˚, 2와 4는 180˚차)상하 및 좌우로 비틀려 운동하고 있어 Cocked 베어링 또는 휜 축인 것이 예상된다. 특히 휜 축인가를 재확인하기 위하여 그림 7-49와 같이 Shaft Stick을 사용하여 축길이 방향으로 베어링 전후에서 동일방향으로 축진동 위상각을 측정하였을 때 역상 (180˚)으로 나타난다.
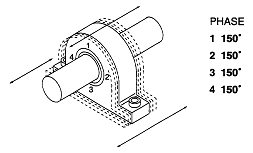
그림 7-47 Planner Motion을 나타내는 축방향 위상각
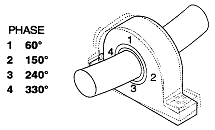
그림 7-48 휜 축 또는 Cocked 베어링에 의한 Twist 상태를 나타내는 축방향 위상각
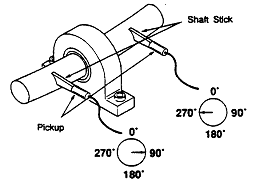
그림 7-49 Bent Shaft 확인용 Shaft Stick의 이용
8.3 不平衡에 의한 位相特性 (Phase Behavior due to Unbalance)
그림 7-50과 같이 원주방향의 4곳에서 위상각을 측정하였을때 위상각이 90˚차가 있으면 통상 불평형 상태이다.
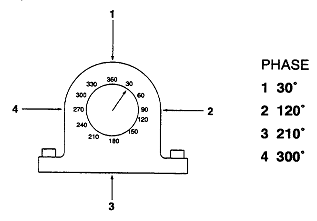
그림 7-50 불평형시의 원주방향 위상각 측정
그림 7-51과 같은 펌프인 경우 불평형 상태가 심하면 1×RPM 진동은 높아야 하고 양쪽 베어링에서 수평방향의 위상차는 수직방향의 위상차와 같아야 한다 (±30˚이내). 그림의 예에서 전동기 베어링에서 수평방향 위상차는(90˚ – 30˚) = 60˚, 수직방향의 위상차는(180˚ – 120˚) = 60˚로 강력한 불평형 상태를 나타내고 있다.
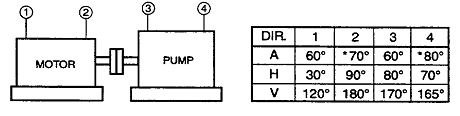
그림 7-51 1×RPM에서의 탁월한 정적 불평형
8.4 弛緩/脆弱에 의한 位相特性 (Phase Behavior due to Looseness/Weakness)
기계부품들이 서로 견고하게 체결되어 있다면 큰 위상차나 진폭차 없이 함께 움직여야 한다. 그림 7-52와 같이 Base Plate와 Concrete Base간에 심한 진폭 및 위상차가 있으면 이들 표면사이에 부적절한 Grouting이 원인이 되어 이완/취약 상태가 예상된다.
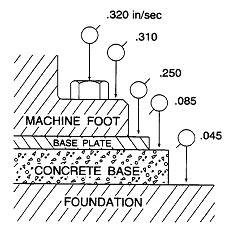
그림 7-52 Looseness에 대한 위상측정
8.5 誤整列에 의한 位相特性 (Phase Behavior due to Misalignment)
Misalignment는 Angular(Face) Misalignment와 Parallel(Rim) Misalignment 2가지 형태가 있다. Shaft Misalignment는 커플링을 전후로 하여 180˚ 위상차를 가지는 특성이 있다. 원주방향의 위상각은 Parallel Misalignment에, 또 축방향 위상각은 Angular Misalignment에 아주 민감하다. 커플링에 인접한 두 베어링에서의 위상각을 측정, 비교할 때 위상자료의 혼동을 피하기 위하여 진동변환기의 설치방향이 일정하여야 하고, 90˚ 간격의 4개의 측정점은 그림 7-53과 같이 동일한 관측방향이어야 한다.
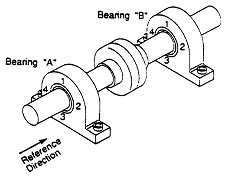
그림 7-53 인접 베어링에서의 위상측정 위치
그림 7-54는 커플링 Misalignment의 한 예로써 간단히 하기 위해 축방향 값만 기록하였다. 전동기 베어링 1과 2 및 Fan 베어링 3과 4는 각기 동상으로 움직이며 따라서 Internal Misalignment, Bent Shaft 또는 Cocked 베어링 징조를 보이지 않고 있다. 그러나 커플링 전후 베어링간의 180˚ 위상변화는 축의 Misalignment 상태를 나타낸다.
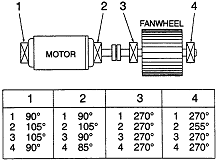
그림 7-54 Angular Misalignment에 관한 축방향 위상각의 비교
대부분의 Misalignment 상태는 Parallel 및 Angular Misalignment의 조합이지 어느 한쪽만 존재하는 일은 거의 없다. 위상값은 서로 꼭 0˚ 또는 180˚ 차이가 나지 않는다. 통상 위상값이 서로 30˚이내에 있으면 대략 동상으로 간주한다.
상당한 위상변화가 축방향이던 원주방향이던 위상차가 180˚에 가까울수록 Misalignment의 가능성은 더욱 높다.
8.6 反力 對 不平衡 檢出 (Detecting Reaction Forces Versus Unbalance)
기계 진동이 1×RPM에서 발생할 때 수평과 수직 방향의 위상 비교로 불평형 상태를 확인할 수 있고 풀리와 기어의 편심, 왕복동력 또는 공진상태 등에 의해 야기되는 반력과 같은 진동에 대한 원인을 규명할 수 있다.
정상적인 불평형 상태는 불평형의 Heavy Spot이 360˚ 회전하면서 동일한 힘을 발생한다. 이로 인해 축 중심선이 기계의 수직 및 수평 방향의 상대 강성에 따라 원형 또는 약간의 타원형으로 움직이게 된다(그림 7-55 참조). 좌우간 기계의 수평방향에서의 최대변위가 발생되기 전에 수직 방향의 최대 변위는 1/4회전 즉 90˚에서 발생된다. 결론적으로 정상적인 불평형 상태에서는 수평방향과 수직방향의 위상차이가 약 90˚ 정도로 나타난다.
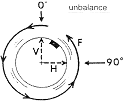
그림 7-55 불평형 상태에서는 수평방향과 수직방향의 위상차이가 약 90˚ 정도 나타난다.
다음으로, 편심된 V벨트에 의해 야기되는 기계의 진동은 벨트 장력의 변화로 인해 나타난다(그림 7-56). 즉, 편심된 Pulley의 상단부가 하단부보다 큰 벨트 장력을 일으켜 풀리가 회전함에 따라 벨트장력의 변동으로 불평형 상태에서와 유사하게 편심된 풀리의 1×RPM과 동일한 주파수에서 진동을 일으킨다. 그러나 불평형 상태와는 달리 편심 풀리에 의한 반력은 풀리가 360˚ 회전하는 동안 균일하게 작용하지는 않는다. 대신에 두 축의 중심선을 지나는 선을 따라 벨트 장력의 방향으로 힘이 발생된다. 이것은 수직방향의 최대변위는 수평방향의 최대변위와 동시에 발생될 수 있다는 것을 의미한다. 결론적으로 그림 7-56에서와 같이 편심된 풀리는 수직방향과 수평방향으로 같은 위상차를 나타낸다(Pickup이 베어링의 어느 쪽에 위치하는가에 따라 180˚가 됨). 하여간 위상은 불평형 상태에서 나타난 위상과는 현저하게 다르게 나타난다. 편심된 기어의 경우도 편심 풀리에서 나타난 수직 및 수평방향의 위상과 유사하며 이때 나타나는 반력은 불평형 상태의 진동과 유사하다. 그러나 이러한 힘은 발란싱으로 교정되지 않는다. 이러한 힘들을 발란싱하면 한쪽 원주방향의 진동은 감소되지만 다른 원주방향의 진동은 증가된다. 즉, 수평방향의 진폭을 감소시키기 위한 발란싱은 수직방향의 진폭을 증가시킨다. 압축기나 가솔린 또는 디젤엔진과 같은 왕복동 기계는 밸브불량이나 분사의 문제 또는 점화 등과 같은 결함으로 인해 1×RPM의 진동이 발생한다. 또한 이러한 진동도 불평형 상태와 유사하게 나타나지만 전적으로 발란싱에 의해 보정될 수 없다. 편심된 풀리나 기어에 의해 야기된 반력과 같이 왕복동 기계의 작동상의 문제로부터 야기된 관성력은 편심에 대해 언급한 바와 같이 수직방향과 수평방향의 위상을 취함으로써 검출될 수 있다.
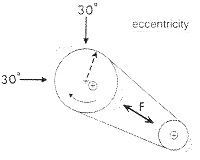
그림 7-56 편심 또는 왕복운동으로 인해 반력이 발생하면
수직방향과 수평방향의 위상차는 0˚ 또는 180˚가 된다.
부가적으로 그림 7-57에서와 같이 왕복동 기계에서는 크랭크축상의 불평형 토오크 반력으로 인해 진동을 야기시킬 수 있다. 이것은 질량 불평형에 의해 야기된 원형이나 타원형의 운동이 아닌 크랭크축 중심선에 대한 기계의 비틀림 진동이나 ‘Rocking’을 일으킨다. 이러한 진동의 비틀림 형태는 종종 크랭크축의 중심선 상하 부분의 수평방향 위상차를 비교하여 검출할 수 있다. 비틀림 진동은 180˚ 다른 위상차를 나타내는 반면에 질량 불평형에 의한 기계의 원형 또는 타원형의 운동은 거의 동일한 위상차를 보여주게 된다.
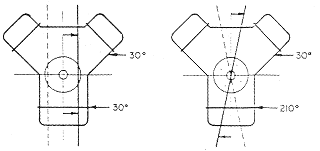
그림 7-57 왕복동 기계의 비틀림 진동은 크랭크 축 상하에서 측정한
진동 위상을 비교함으로써 불평형과 구별할 수 있다.
8.7 共振 糾明 (Resonance Determination)
앞에서 Bode Plot과 Polar Plot에 대해 논술하였고 몇 가지 예를 들면서 기계의 기동 또는 정지시 위상은 기계의 공진 주파수를 검출하고 규명하는데 도움된다고 하였다. 단순 공진은 기계의 속도가 공진 주파수를 통과할 때 위상이 180˚ 이동될 것이다. 만약 기계가 공진점 근처에서 운전되고 있다면(수평 방향의 베어링이 공진 한다고 하면) 수평 및 수직방향에 대한 위상비교를 통하여 확인할 수 있다. 앞에서 논의된 것처럼 대개의 불평형 조건은 일반적으로 수평과 수직 위상 차이가 약 90˚이다. 그러나 만약 기계가 수평 또는 수직 공진 주파수에서 진동하고 있다면 수평 및 수직 방향의 위상은 베어링 픽업 설치위치에 따라 동일하거나 180˚ 반대값이 될 것이다. 이와 같은 상대위상의 뚜렷한 90˚ 오차는 공진 조건에 의해 야기된 90˚ 위상 지연의 결과이다.
9. Full Spectrum 분석 (Full Spectrum Analysis)
9.1 Spectrum과 Full Spectrum
100여년 전에 Jean Baptiste Fourier 남작은 반복성이 있는 파형이라면 그 어떤 것이라도 사인파를 합성하여 만들어낼 수 있다는 점을 증명하였는데 이것을 바꾸어 말하면, 어떤 신호든지 이러한 사인파들로 분리해낼 수 있다는 말이다.
그림 7-58은 두 개의 사인파를 합성하여 만들어진 간단한 파형을 보여준다.
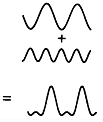
그림 7-58 실제 파형은 사인파를 합성하면 만들어 질 수 있다.
전통적으로 사람들은 시간영역에서 신호를 관찰해 왔다. 시간영역 자료는 어떤 변수가 시간에 따라 어떻게 변했는가에 대한 기록이다. 그림 7-59A는 이러한 사인파들을 삼차원 그래프로 나타낸 것이다. 서로 직각을 이루는 세 개의 축은 진폭, 시간, 주파수 축이다. 이 그래프를 시간과 진폭의 관점에서 보면 시간영역에서 자료를 관찰하는 것이 되고, 이는 사인파들의 합을 보게되는 것이다 (그림 7-59B).
만일 이 그래프를 주파수와 진폭의 관점에서 보면 자료를 주파수 영역에서 관찰하는 것이 되고, 시간영역에서 보는 것과는 완전히 다른 그림을 보게되는데 흔히 이러한 Plot을 Spectrum Plot이라고 부른다 (그림 7-59C). 주파수 영역에 나타나는 모든 사인파는 마치 이 사인파를 그 진행방향의 끝에서 바라본 것처럼 하나의 수직선으로 나타나는데, 이 수직선의 크기는 진폭을 나타내고, 그 위치는 주파수를 나타낸다.
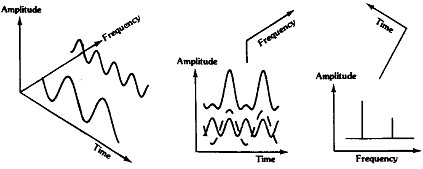
A) 시간, 주파수 및 진폭을 B) 시간영역에서 본 것 C) 주파수영역에서 본 것 나타내는 3차원 좌표
그림 7-59 시간 영역과 주파수 영역간의 관계
최근 들어 세계적으로 Full(Plus And Minus) Spectrum Plot에 대한 관심이 증대되고 있다. Full Spectrum에 대한 연구는 벤틀리 네바다사(Bently Rotor Dynamics Research Corporation, Bently Nevada Corporation)에서 하고 있는 연구 외에 한국에서 연구중인 “Directional Power Spectrum”과 중국에서 연구중인 “Holo Spectrum” 등이 있다.
Fast Fourier Transform (FFT)은 하나의 신호를 그 신호를 구성하고 있는 각 주파수 성분으로 분해하는 방법중의 하나로서, 자료를 시간영역에서 주파수 영역으로 바꾸는 수학적인 연산방식이다. 오늘날의 Microprocessor는 소형이지만 FFT를 수행하는데 충분한 성능을 가지고 있다. FFT를 수행하기 위해 입력, 계산과정, 계산결과를 나타내는데 복소수가 이용된다. 복소수는 Direct(Real) 부분과 Quadrature(Imaginary) 부분으로 구성되어 있다 (그림 7-60).
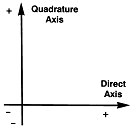
그림 7-60 복소수 축
보통 무시되지만, 한가지 흥미있는 것은 FFT의 특징이 주파수 영역의 출력이 실제로 양(Positive)의 주파수 성분과 음(Negative)의 주파수 성분을 모두 포함하고 있다는 것이다. 하나의 진동 변환기에서 수집된 시간영역 신호가 FFT 분석장비로 입력될 때, 그 신호는 일반적으로 Direct 부분의 입력으로 되고, Quadrature 부분의 입력은 “0”으로 설정된다. 이렇게 되면, FFT 분석장비는 음 주파수 부분의 스펙트럼이 양 주파수 부분의 스펙트럼과 동일한 스펙트럼을 만들게될 것이다. 이런 상황은 일반적인 경우인데, 이런 이유로 음의 주파수는 양의 주파수와 중복되는 정보를 가지게 되고 그래서 쓸모 없는 정보로 간주되어 무시되게 된다.
그러나 만일 Direct와 Quadrature 복소수 축(그림 7-60)을 눈여겨본다면 이 둘의 관계는 XY 진동 변환기와 동일하다는 것을 발견하게 된다. 만일 X와 Y 변환기에서 자료를 동시에 수집하고, X Probe에서 수집한 자료는 FFT 분석장비의 Direct 부분 입력으로, Y Probe에서 수집한 자료는 Quadrature 부분의 입력으로 연결한다면 어떤 결과가 나타날 것인가? 이런 경우에 양 및 음의 주파수는 서로 같은 모양이 아니며, 음의 주파수 부분은 양의 주파수 부분과 동일한 중복되는 정보가 아닌 필요한 부가적인 정보를 포함하게 된다.
간단히 말해, Orbit이 시간 영역에서의 파형(Waveform)과의 관계처럼 Full Spectrum은 주파수 영역에서의 보통 이야기하는 Spectrum과의 관계와 같다. Spectrum이나 시간영역 파형 Plot은 Probe 하나에서의 입력신호만 있어도 Plot을 만들 수 있지만, Orbit이나 Full Spectrum Plot은 서로 직각으로 설치되어 있는 두 개의 Probe로부터의 입력신호가 있어야 Plot을 만들 수 있다. Orbit과 Full Spectrum Plot은 이렇게 직각으로 설치된 Probe로부터의 신호를 받아 Orbit의 모양이나 진동의 회전방향 등과 같이 Spectrum이나 시간영역 파형에서는 알 수 없는 정보를 제공해준다. 만일 진동의 회전방향을 축의 회전방향과 비교해 보면 진동의 세차운동 방향을 알 수 있다. 보다 신뢰성 있는 기계상태에 대한 진단 및 분석을 위해서는 사전에 두 가지 기본 특성인 Orbit의 타원된 정도와 진동의 세차운동 방향을 알고 있어야 한다.
단일 주파수 성분의 타원형 Orbit은 축의 회전방향과 같은 방향으로 회전하는 진동 성분과 반대방향으로 회전하는 진동 성분으로 구성될 수 있다.
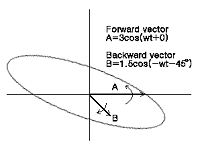
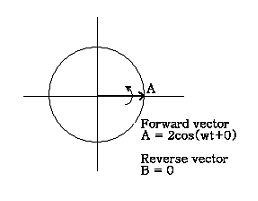
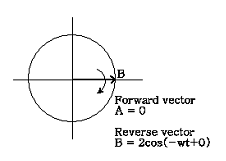
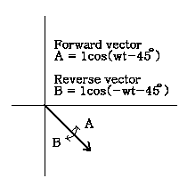
만일 벡터 A와 B가 동일 주파수로 서로 반대방향으로 회전하고 있다면 직교좌표에서 이 벡터들의 합은 타원으로 나타난다. Orbit의 타원 정도와 세차운동 방향은 A 벡터와 B 벡터 사이의 진폭에 따라 달라지고, 타원의 주 진동축의 회전방향은 A 벡터와 B 벡터의 위상에 따라 달라진다. 그림 7-61은 이에 대한 간단한 예를 보여준다.
Full Spectrum을 이용하여 기계상태를 진단할 때도 반대방향만 제외하고는 동일한 개념을 적용할 수 있다. 실제 기계는 Orbit에 나타나는 것과 동일하게 움직인다. 축의 회전방향과 같은 방향으로 회전하는 진동성분인 벡터 A와 반대방향으로 회전하는 진동성분인 벡터 B는 각각 동일한 Orbit을 만들어내는 FFT 계산의 결과이다.
여기서 두 가지 약속 사항이 있다.
① 회전방향[시계방향(CW)과 반시계 방향(CCW)]은 별도의 표시가 없는 한 원동기에서 종동기를 바라본 방향을 기준으로 정한다.
② 진동의 회전방향과 축의 회전방향이 같을 경우에는 정방향 세차운동(Forward Precession)이 일어나고 있는 것이고, 회전방향이 서로 다를 경우에는 역방향 세차운동(Reverse Precession)이 일어나고 있는 것이다.
Full Spectrum은 새로운 기술적인 진보라고 할 수 있다 (그림 7-62). Full Spectrum은 우리가 보통의 Spectrum에서 얻을 수 있는 것보다 더 많은 정보를 제공해준다. 그림 7-62는 정방향 및 역방향으로 회전하는 원형, 타원형 및 과도한 Preload를 받고 있는 기계의 Orbit/Timebase, Full Spectrum과 일반 Spectrum Plot을 보여준다.
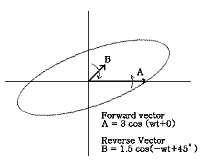
(A) (B)
(C) (D)
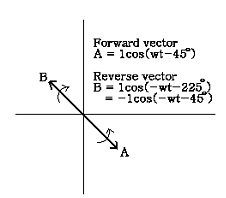
(E) (F)
그림 7-61 Orbit의 타원 정도는 정방향 및 역방향의 진동성분에 따라 다르다
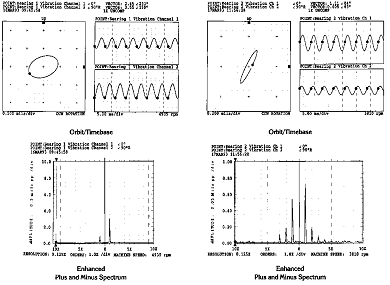
(예 1) (예 2)
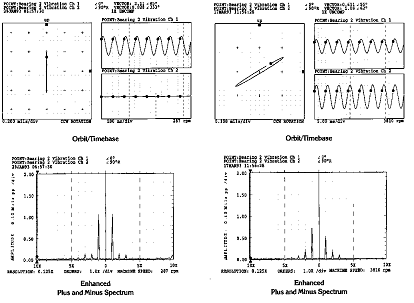
(예 3) (예 4)
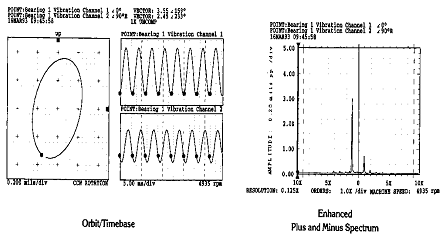
(예 5)
그림 7-62 Orbit 및 Full Spectrum 비교
보통의 Spectrum 대신 Full Spectrum을 사용하면 다음과 같은 4가지 주요한 이점이 있다.
① Preload의 존재 여부, 기계의 상태, Orbit의 타원된 정도를 알 수 있다.
② 모든 진동 성분의 회전방향을 알 수 있다.
③ 비동기 진동성분을 포함하고 있는 Orbit의 경우에도 특정 성분의 진동 회전방향을 쉽게 알아낼 수 있다. 이러한 점은 Orbit/Timebase 기술을 상당히 확대시킨 것이라 할 수 있다.
④ Orbit/Timebase 또는 Digital Vector Filter 등과 같은 다른 방법을 이용해서 알게된 진동의 회전방향은 얻은 정보를 확인하는데 이용될 수 있다.
하나의 변환기로 측정한 자료를 이용하여 작성된 Timebase Plot과 보통의 스펙트럼 Plot은 서로 일치되는 결과를 나타내며 동일한 정보를 제공해준다.
Orbit/Timebase Plot이 기계의 이상상태 진단에 있어서 매우 중요하긴 하지만, Full Spectrum Plot은 부가적인 도구로서 거기에 더하여 유용한 정보를 제공해 준다.
다음에는 유체에 의해 유발되는 불안정(Fluid-Induced Instability), Rub, Preload, Misalignment, Shaft Crack 및 Split Critical 등에 대해 Full Spectrum Plot을 이용한 기계의 진단 및 분석에 대해서 이야기 하고자 한다.
9.2 流體 誘導 不安定 (Fluid-Induced Instability)
보통 Oil Whirl 또는 Oil Whip으로 불리는 유체 유도 불안정은 시스템의 기계적인 공진과 관련된 Direct Dynamic Stiffness와 시스템의 유체 공진과 관련된 Quadrature Dynamic Stiffness가 동시에 “0”이 될 때 나타나는 특별한 두 공진 상태이다. 원래 Direct Dynamic Stiffness는 Mass Stiffness항과 Spring Stiffness항이 서로 크기가 같고 방향이 서로 반대일 때(K=Ω2M) “0”이 되며, 이때에는 오직 Quadrature Dynamic Stiffness만이 시스템에 작용하는 유일한 항이 된다. Quadrature Dynamic Stiffness항은 ω ≈ λΩ일 때 “0”이 되며, 이때에는 Direct Dynamic Stiffness만이 시스템에 작용하는 유일한 항이 된다.
여기서 M=Rotor Mass, K=Spring Stiffness, Ω=Rotative Speed, λ=유막의 평균 속도, ω=Rotor 회전 각속도 이다.
Direct Stiffness와 Quadrature Stiffness가 동시에 “0”이 될 때, 시스템은 자체의 기계적 공진점과 유체 공진점에서 운전되게 되고, 이때 시스템의 움직임을 억제하는 힘이 하나도 없게되어 시스템이 불안정해진다. 이런 불안정한 상태는 축이 베어링이나 Seal 간극에 접근하게 되면 곧바로 새로운 힘의 균형이 이루어진다.
기계를 진단하는 견지에서 보면 유체 유도 불안정 진동은 항상 축의 회전방향으로 작용하는 Fluid Wedge Support Force의 접선방향 성분에 의해 유발된다. 유체 유도 불안정 진동의 가장 두드러진 특징은 진폭이 크고 진동의 λΩ 부근의 주파수에서 정방향으로 회전하는 진원이거나 또는 진원에 가까운 Orbit이다. 그러나 λ가 축의 편심, 베어링이나 Seal의 형상, 표면 거칠기, 유입되는 유체의 조건 등과 어떤 선형적인 관련이 없기 때문에 유체 유도 불안정 진동의 주파수가 바뀔 수 있으나, 일반적으로 Whirl 불안정 진동의 경우에 진동 주파수는 1/2× 보다 조금 작다.
그림 7-63은 약 2300 rpm 부근에서 유체 유도 불안정 진동이 시작되는 반시계 방향으로 회전하는 어떤 기계의 Full Cascade Plot을 나타낸다. 이 기계에는 유체 유도 불안정 진동이 발생하는 위치인 베어링 Outboard에 서로 직각(0˚ 및 그 90˚ 우측)으로 설치된 두 개의 변위 센서가 있다. 그림 7-64와 7-65는 Whirl (2790 rpm)과 Whip (4890 rpm)이 발생한 상태의 Orbit/Timebase Plot이다.
여기서 주목할 것은 Oil Whirl이나 Whip의 경우 모두, Orbit이 원형이고 진폭이 크며 또 정방향 세차운동을 한다는 점이다 (축은 반시계 방향으로 회전하고 수평방향 진동성분이 수직방향 진동성분보다 위상이 약 90˚ 가량 앞선다). Full Cascade Plot을 보면 이점을 확인할 수 있는데 약 4500 rpm이하의 속도에서는 진폭이 크고 정방향 진동성분이 거의 대부분을 차지하고 있다. 역방향 진동성분이 존재하지 않은 것은 Orbit이 원형이고 그 회전방향이 정방향임을 의미한다. Whirl의 경우에 유체 유도 불안정 진동 주파수는 약 0.45×이고, 축의 회전속도가 약 5000 rpm에 이르러 시스템이 Whip 상태로 변화하게 되면 진동 주파수는 0.45×에 더 이상 고정되지 않게 된다. Whip 상태(그림 7-65)에서는 Orbit의 모양이 약간 타원형이고, 이러한 사항은 Full Spectrum Plot에서 기계 회전속도가 약 4500 rpm이상에서 그 크기는 작지만 역방향 진동성분이 존재한다는 점에서 확인할 수 있다.
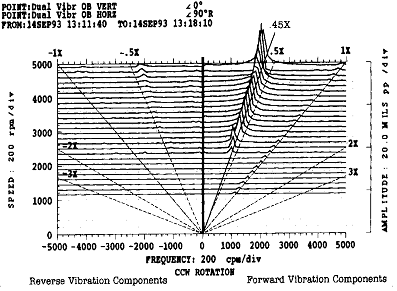
그림 7-63 유체 유도 불안정 진동
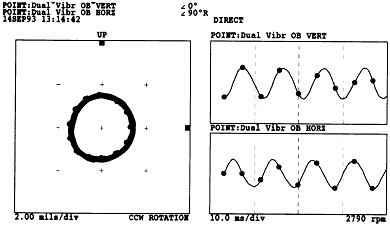
그림 7-64 유체 유도 불안정 진동 : Oil Whirl이 발생하면 정방향 세차운동을 하며
원형 또는 거의 원형에 가까운 Orbit이 나타난다 (2790 rpm).
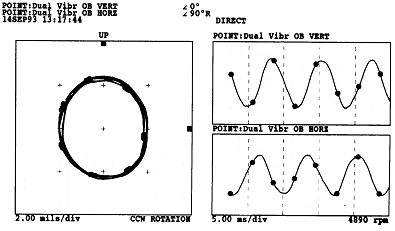
그림 7-65 유체 유도 불안정 진동 : Oil Whip이 발생하면 정방향 세차운동을 하며
원형 또는 거의 원형에 가까운 Orbit이 나타난다 (4890 rpm).
9.3 Rub
Rub는 2차적인 고장으로 분류된다. Rub는 스스로 발생하는 것이 아니고 항상 무엇인가 다른 원인의 결과로 나타난다. 간극이 너무 작거나 혹은 클 때, 중력이나 Misalignment, Gear Mesh, 유체의 유동 등과 같은 원인으로 나타나는 과도하거나 부적절한 Preload, Balancing이 제대로 되어있지 않은 Rotor, 변형된 Casing 등과 같은 것들도 Rub을 일으키는 요인이 될 수 있다. 기계에서 나타나는 진동신호는 여러 요인들이 복합되어 그 결과로 나타나기 때문에 기계에서 나타나는 진동신호만으로 Rub가라고 진단하는데는 어려움이 있다. 기계상태에 영향을 미칠 수 있는 여러 요인중 어느 한 요인의 작은 변화라도 기계에는 급격한 변화를 일으킬 수 있다. Rub이라도 나타나는 신호가 Wiping에 의한 것인지, Impact 및 그 반동으로 인한 것인지를 생각해봐야 하고, 그 정도가 심각한지 또는 경미한지, 윤활이 되고 있는 상태인지 비윤활 상태인지, 부분 Rub인지 전원주 방향에 걸친 Rub인지?, 만일 전원주 방향에 걸친 Rub이라면, 그 세차운동 방향이 정방향인지 역방향인지, Rub가 발생하는 동안에 로터의 강성이 더 강해지는 유형인지 또는 더 약해지는 유형인지? 공진 주파수와 관련이 있는 기계의 회전속도는 얼마이며, 그때의 속도는 공진 주파수 보다 낮은지 혹은 높은지? 또는 두배 이상인지? 등
여러 가지 형태의 Rub으로 인해 기계에서 나타날 수 있는 다양한 형태의 응답은 다양한 기법과 도구들이 필요하게 됨을 의미한다. Rub 상태에 대해 신뢰할 만한 진단을 하기 위해서는 Orbit, Shaft Centerline Position, Bode, Polar, Spectrum/Full Spectrum Plot 등을 모두 검토해야만 한다. Full Spectrum Plot에는 축의 회전방향과 반대방향으로 회전하는 진동 성분이 나타나기 때문에 역방향 진동 성분을 발생시키는 마찰이 큰 Rub을 진단하는데 매우 유용하게 이용될 수 있다. 그림 7-66과 7-67은 Full Spectrum Cascade Plot의 예이다.
기동․정지 과정에서 나타난 역방향 세차운동을 하는 전 원주방향 Rub의 경우에 대한 Full Spectrum Cascade Plot이 그림 7-66과 7-67에 나타나 있다. 전 원주방향 Rub가 발생하고 있는 상태의 Orbit은 일반적으로 원형이고 베어링이나 Seal 크기만큼 크다. 이때 나타나는 진동의 주파수는 축이 베어링이나 Seal과 접촉할 때 강성이 증가되기 때문에 고유 진동수가 변하는데 이는 회전속도와는 무관하다. Orbit의 모양과 그 회전방향은 Full Spectrum Cascade Plot을 통해서 확실히 확인할 수 있다. 시스템의 변경된 고유 진동수를 쉽게 알 수 있다. 그러나 이 두 Plot만으로는 Non-Rub인 경우의 고유 진동수를 찾아내거나 베어링이나 Seal 간극을 확인하기에는 충분한 정보를 얻을 수 없다.
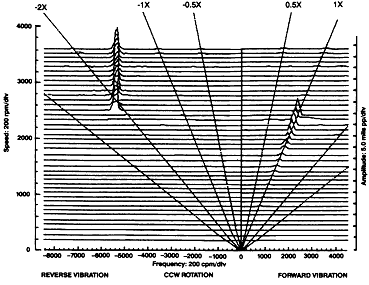
그림 7-66 기동중에 나타난 전 원주방향 Rub
앞서 언급한 역방향 세차운동을 하는 전 원주방향 Rub가 매우 드물게 발생하긴 하지만, 한번 발생할 경우 그 결과는 매우 파괴적이다. 유능한 기계 진단자는 빠르고 정확하게 이런 Rub 상태를 감지할 수 있어야 한다. 모든 역방향 세차운동을 하는 진동성분이 항상 나쁘다거나 그 역방향 진동 성분이 항상 Rub 때문에 발생한 것이라고 생각해서는 안된다는 말은 모두 사실이 아니다. 자세한 사항은 다음에 나오는 Split Critical (Resonance) 참조.
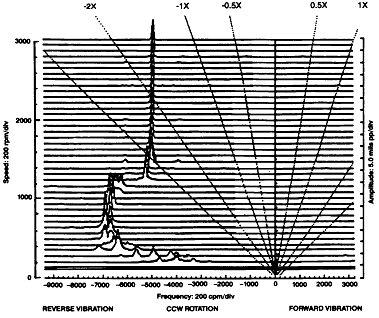
그림 7-67 정지중에 나타난 전 원주방향 Rub
9.4 Preload 및 Misalignment
Preload는 로터 시스템에 작용하는 방향 및 크기가 일정한 힘이다. 가장 일반적인 Preload는 중력이다. 그 외에 Preload를 발생시키는 다른 요인으로는 내적 및 외적인 Misalignment, 공정중에 발생하는 힘, 유체 공학적 힘, 베어링 형상, 파이프 응력, 차동 팽창 등이 있다. Preload를 신호로 감지할 수 있는지 여부는 기계의 종류나 그 심각한 정도, 공정상의 상태 및 운전속도와 공진 주파수와의 관계 등에 따라 다르다. 명확한 신호가 나타나지 않을 수도 있다. 축에 Preload를 가하게 되면, 베어링 간극내에서 축의 편심위치가 변하게 되며 이로 인하여 시스템의 강성이 변하게 된다. 강성의 증가로 인해 기계의 안정성이 변화될 수 있고 그로 인하여 종종 기계의 진동이 감소될 수도 있다. 보통 진동이 낮은 것이 좋은 상태라고 알려져 있지만, 만일 진동치가 낮게 나오는 것이 심각한 Misalignment에 의한 결과일 경우에는 바람직한 것이 아니다. 높은 반경방향 Preload는 축이 비선형 강성구역에서 운전되게 만드는데, 이것은 진동신호의 조화성분을 발생시키고 보통 2× 성분이 나타난다.
Preload를 조사하는데 최우선으로 사용되는 Plot은 Orbit과 Shaft Centerline Position Plot이다. Full Spectrum Plot은 Preload 문제가 의심될 때 다른 Plot에서 얻은 정보를 확인하는 목적으로 가장 많이 사용된다. 그림 7-68은 Preload를 받고 있는 축에 대해 정방향으로 회전하고 타원형이며 1× 성분이 주성분인 Orbit/Timebase Plot을 보여준다. 이러한 사항은 Full Spectrum Cascade Plot을 통해 확인할 수 있다 (그림 7-69). Full Spectrum Cascade Plot에는 기계가 기동되는 전과정에 걸쳐 정방향으로 회전하고, 타원형이며 1×가 주성분인 동일한 모양의 Spectrum Plot이 연속적으로 나타난다는 점에 주목하라.
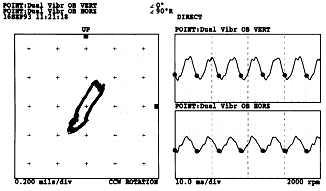
그림 7-68 Preload를 받고 있는 축의 Orbit/Timebase Plot
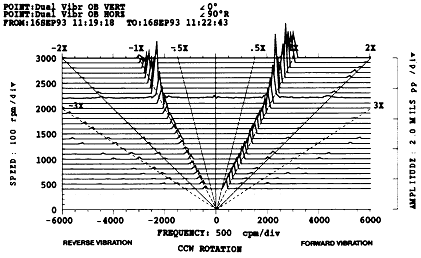
그림 7-69 Preload를 받고 있는 축의 Full Spectrum Cascade Plot
9.5 Shaft Crack
축에서 어느 한 방향의 강성이 그 방향과 수직인 방향의 강성보다 더 강한 비대칭 강성이 나타나는 원인으로는 기하학적인 형상(Keyway, 완전한 원형이 아닌 단면 등)이나 제작상 또는 유지정비 과정에서의 문제(잘못되었거나 부적당한 끼워 맞춤) 또는 축균열과 같은 것이 있다. 비대칭성 강성을 가진 수평축을 어느 한 점에서 관찰하면 강성이 강해졌다가 약해지는 과정이 반복되는 것을 볼 수 있다. 축에 있어서의 이러한 강성 변화는 Preload의 크기에 따라 축이 한번 회전하는 동안 축이 많이 휘고 적게 휘고, 많이 휘고 적게 휘는 과정을 반복하게 된다. 이렇게 축이 한번 회전하는 동안 변위가 두 사이클 변화함에 따라 2× 신호가 발생되게 된다. 이러한 2× 진동성분은 마치 강성의 변화가 없는 것처럼 선형성을 가지며, 정방향 세차운동을 하는 원형 Orbit이 나타나고 2× 공진영역에서 1× 진동보다 더 크게 나타날 것이다. 통계적으로 보면 약 75% 정도의 경우에 있어서는 운전속도에서 1× 거동만 나타난다.
기계진단의 관점에서 볼 때, 축 균열은 축 균열에 관한 제1법칙 및 제2법칙을 적용해보면 감지해낼 수 있다. Cascade, Full Spectrum Cascade, Orbit, Polar, Acceptance Region, Bode Plot은 축 균열을 탐지할 때 기본적으로 사용되는 Plot들이다.
축균열 제1법칙 (1st Rule of Shaft Cracks)
축에 균열이 발생되면 거의 확실히 축이 휘게된다.
① Acceptance Region 및 APHT Plot에서 보면 1× 및 2× Vector에 있어서 예기치 못한 진폭 또는 위상변화가 나타난다.
② 축이 휘게되면 기계적 및 전기적인 Runout과 함께 그 영향이 1× Slow Roll 벡터로 나타나게 된다. 오랜 동안 동일한 상황하에서 측정했을 때 1× Slow Roll 벡터는 특별한 이유 없이 변하지 않아야 한다. 참고로 각 기계에 대한 1× Slow Roll 벡터에 대한 기록 사항은 잘 보존해야 한다. 1× Slow Roll 벡터의 현저한 변화는 면밀히 조사되어야만 하고 축 균열이 아닌가 의심해 보아야 한다.
축균열 제2법칙 (2nd Rule of Shaft Cracks)
축의 강성이 비대칭이고 반경방향으로 가해지는 Preload를 가지고 있는 축이 공진 주파수의 약 1/2에 해당하는 속도로 회전하고 있을 때 높은 2× 진폭과 2× 위상 변화가 나타날 수 있다.
① 축이 공진 주파수의 약 1/2 부근의 속도로 회전하고 있고 2× 진동을 일으킬 만한 가진력이 존재할 때 공진 주파수가 가진되게 된다. Full Spectrum Cascade Plot(그림 7-70)은 약 1300~1400 rpm에서 2× 진폭의 Peak치를 보여준다. 이 기계에서는 3×와 4× 성분도 나타나고 있음에 주목하라. 3× 진동 진폭의 Peak치는 약 900 rpm에서 나타나고, 4× 진동 진폭은 약 700 rpm에서 나타난다. 이 기계의 1차 공진속도는 약 2700 rpm이다
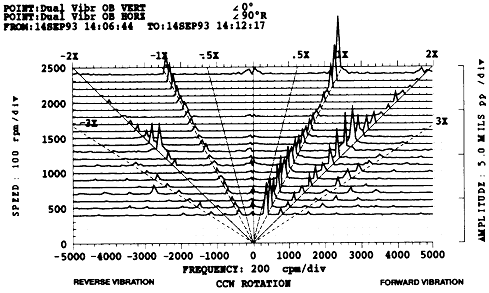
그림 7-70 기동시에 Shaft Crack 징후가 나타난 Full Spectrum Cascade Plot
② 1차 공진 주파수의 1/2 근방인 1390 rpm에서 운전중일 때, Direct Orbit(그림 7-71)과 Slow Roll 값이 보상된 1× Orbit(그림 7-72), Slow Roll 값이 보상된 2× Orbit(그림 7-73), Full Spectrum Plot(그림 7-74)에 나타난 정보를 종합해보면 다음과 같은 사항을 발견할 수 있다.
• 1× 진동성분은 진동 회전방향이 정방향이고 Orbit 모양은 약간 타원형이다.
• 2× 진동성분은 진동 회전방향이 정방향이고 Orbit은 1× 보다 약간 더 타원형이며 1× 성분보다 진폭이 더 크다.
• Direct Orbit에 나타나는 Internal Loop는 같은 방향으로 회전하는 두 가지 진동성분을 포함하고 있는 신호를 가지는 특성이 있다.
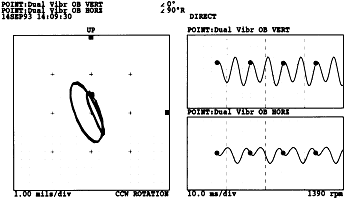
그림 7-71 1390 rpm에서 Shaft Crack 징후가 나타난 Direct Orbit Plot
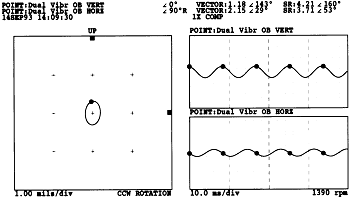
그림 7-72 1390 rpm에서 Shaft Crack 징후가 나타난 1× Orbit Plot
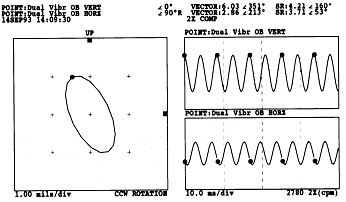
그림 7-73 1390 rpm에서 Shaft Crack 징후가 나타난 2× Orbit Plot
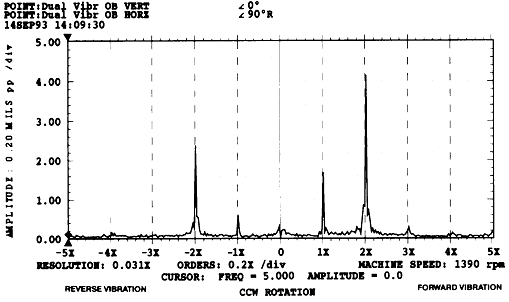
그림 7-74 1390 rpm에서 Shaft Crack 징후가 나타난 Full Spectrum Plot
9.6 Split Critical
기본 동기 Rotor 응답으로부터 간단한 Rotor의 공진 주파수를 알 수 있다.
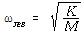 ω = 공진 주파수, K = 강성, M = 질량
ω = 공진 주파수, K = 강성, M = 질량
기계의 강성이 다른 방향보다 어느 한 방향으로 강할 경우에 기계의 공진 주파수가 강성이 강한 방향에서는 더 높고, 강성이 약한 방향에서는 더 낮을 것이라는 것을 예상할 수 있다. 실제로 이러한 현상은 사실상 모든 기계에서 나타난다. 베어링 지지 상태, 기계 기초, 배관으로부터의 영향이 포함된 시스템 강성은 거의 전방향에 걸쳐 동일하지 않다.
그림 7-75는 축이 시계방향으로 회전하는 기계의 Outboard 베어링에 직각(0˚ 및 90˚)으로 설치되어 있는 두 개의 변위 측정기에서 얻어진 Data를 가지고 작성된 Bode Plot을 보여준다. 수직방향(0˚)으로 설치되어 있는 센서로부터 측정된 축의 1차 공진속도는 2,230 rpm이고, 수평방향(90˚)으로 설치되어 있는 센서로부터 측정된 축의 1차 공진속도는 2,350 rpm이다.
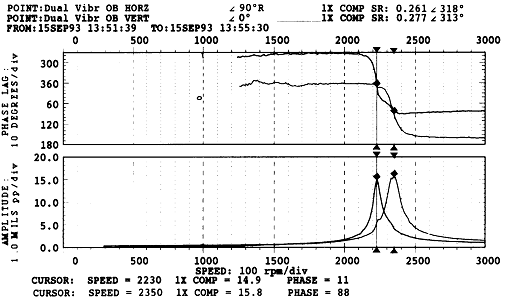
그림 7-75 Split Critical이 잘 나타난 Bode Plot
두 Probe에서 얻어진 Data를 기준으로 작성된 Bode Plot을 비교하여 위상지연을 검토해 보면, 2230 rpm 이하와 2350 rpm 이상에서의 진동의 회전방향은 정방향 즉, 수직방향에서 측정한 진동의 위상이 수평방향에서 측정한 진동의 위상보다 앞서나, 2230 rpm과 2350 rpm 사이에서의 진동의 회전방향은 역방향 즉, 수평방향에서 측정한 진동의 위상이 수직방향에서 측정한 진동의 위상보다 앞서는 것으로 나타났다. 이러한 역방향 진동성분은 나쁜 것이 아니며 기계에 아무런 이상점도 없었다. 역방향 진동성분은 축의 강성이 비대칭인 관계로 나타난 것이고, 흔히 발생하는 현상이다.
Full Spectrum Cascade Plot(그림 7-76)과 1× Orbit/Timebase Plot(그림 7-77, 7-78, 7-79)은 이런 분석결과를 확인하기 위해 사용된다. 1× 진동의 회전방향은 약 2300 rpm 부근에서의 잠시동안만 제외하고는 기동과정 전체에 걸쳐 모두 정방향으로 나타났다 (이는 1× 진동성분중 정방향으로 진동하는 성분이 역방향으로 진동하는 성분보다 크다는 것을 의미함). 정방향으로 회전하는 1× 진동성분의 Peak는 수직 및 수평방향에서의 임계 주파수(Critical Frequency)에 따라 2200 rpm과 2400 rpm에서 나타났으며, 역방향 1× 진동성분의 Peak는 2300 rpm에서 나타났다.
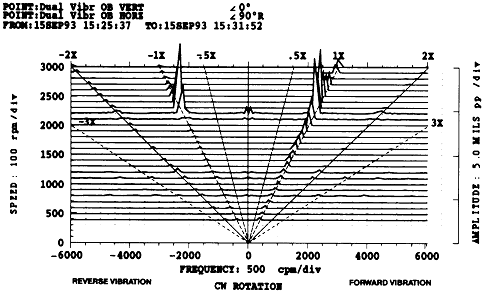
그림 7-76 Split Critical이 나타난 Full Spectrum Cascade Plot
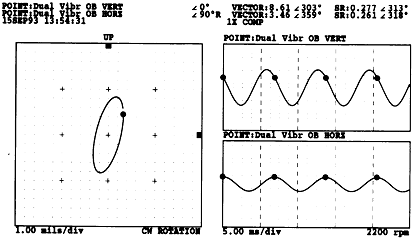
그림 7-77 2200 rpm때의 1× Orbit/Timebase Plot
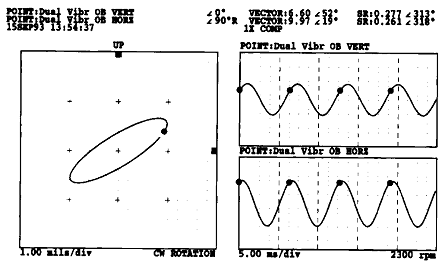
그림 7-78 2300 rpm때의 1× Orbit/Timebase Plot
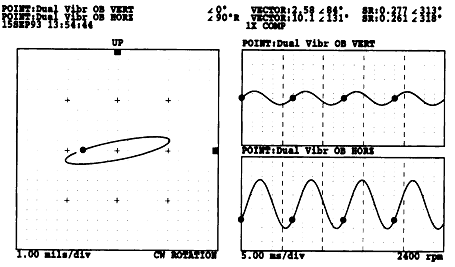
그림 7-79 2400 rpm때의 1× Orbit/Timebase Plot
