Signal Processing
1. Decibel 단위와 대수 척도 (Decibel Units and Log Scale)
4. AC에서 DC로의 변환 (AC to DC Conversion)
5. 자료의 질을 향상시키기 위한 신호 처리 (Signal Processing for Data Enhancement)
기계 상태 감시에 사용되는 모든 장비는 어떤 형식이든지 신호 조절 기능을 갖추고 있다.
상태 감시 장비의 성능과 특징을 이해하기 위하여 기계 분석자들은 Filters, 적분기, AC에서 DC로의 변환 등과 같은 신호 조절을 하는데 있어서 자주 접하게 되는 기본 원리들은 물론 용어에 익숙해지는 것이 중요하다.
1. Decibel 단위와 대수 척도 (Decibel Units and Log Scale)
Decibel(dB)은 진동 진폭의 측정값이나 더 정확하게는 측정된 진폭과 가속도와 속도 값에 대한 기준 규격 값과의 비율이며 보다 일반적인 의미로는 dB 척도(Scale)는 어떤 비율을 표현하는데 사용되는 로그 함수적인 척도이다. 일반적으로 dB로 표현되는 매개변수는 한 개의 장비에 의하여 동시에 수용될 수 있는 가장 크고 가장 작은 진폭 신호 사이의 비율을 나타낼 수 있는 역학적 범위(Dynamic Range)이다. 역학적 범위는 데이터 수집기나 분석기, 기록 장치와 같은 기계 감시 및 분석에 사용되는 장비를 선정하는데 중요한 기준이 된다.
진동에서 사용되는 척도로는 2가지가 있는데 하나는 선형적인 것이고 다른 하나는 대수적인 것이다. 선형적인 것은 사용하기가 쉽고 측정된 값은 큰 어려움 없이 다른 값들과 비교할 수 있다. 그러나 이것을 대수척도로 바꾸면 쉽게 식별할 수 있는 선형성이 없어진다. 한편 대수척도는 변화하는 값들에 대한 많은 정보를 작은 공간 내에 삽입할 수 있고 때로는 평균화함으로써 신호 대 잡음비(Signal to Noise Ratio)의 질을 향상시킨다. 좋은 신호 대 잡음비를 가진다는 것은 낮은 신호도 계측기 시스템의 기본 잡음에서도 검출할 수 있다는 것이다. 여기서 잡음이란 전기적인 잡음이지 음향 소음이 아니다.
많은 사람들이 Log와 Decibel(dB) 술어에 대하여 공포심을 가지고 있는데 특히 데시벨 값은 음향 기술자만이 사용하는 음향 측정단위라고 생각하기 때문이다. 물론 음향학에서 데시벨 척도를 사용하지만 물리학에서 처음으로 발생되었고 전기적 술어로써 주로 사용되고 있다.
학술적으로는 dB은 벨(BeL)의 1/10이고, 입력(또는 기준치)에 대한 출력(또는 측정치) 비율의 상용대수에 로그를 취한 것에 10배(전력인 경우) 또는 20배(음압, 전압 및 전류인 경우)를 곱한 것이다. 출력이 입력과 같을 때는 Log 1=0 즉 0 dB이 된다. 다르게 표현하면 dB 척도에서의 Zero는 입력(기준치)과 출력(측정치)이 같을 때이다. 이와 같이 dB 측정값은 입력 값이나 기준 값으로부터 벗어난 정도 또는 편차를 로그함수 형식으로 표시한 것이다.
전력 계통에서 공급 시스템이 10 dB 감도를 가진다는 것은 비율로는 10:1 이다. 기준 전력이 100 ㎾라면 출력이 1,000 ㎾이다. 즉 dB=10 Log(1,000/100) = 10 log(10) = 10(1) = 10 이다. 증폭기가 20 dB 감도를 가졌다면 이 증폭기는 입력의 102 또는 100배 출력이 발생한다.
음압, 전압 및 전류는 왜 20Log를 기준하고 있는 것일까? 전력은 Impedance (Resistance)가 같거나 일정하면 전압의 제곱에 따라 변한다. 전력(Watt)=E2/R이므로 dB=10 Log(측정치E/기준치E)2=(10)(2)Log(측정치E/기준치E)=20Log(전압비)이다.
40 dB의 감도 편차를 두고 한사람은 100:1, 다른 사람은 10,000:1 이라고 말할 때 전자는 전압 기준이고 후자는 전력 기준이기 때문이다.
원동기의 진동은 변환기나 진동 분석 장비에 의해 검출 및 분석되며 또한 이들 장비에서는 전압(mV)에 의해 처리되므로 dB=20 log(전압비)가 적용된다. 따라서 전압 비가 10이면 20 dB, 전압비가 2이면 6 dB 또 전압비가 ![]() 이면 3 dB이다.
이면 3 dB이다.
다음과 같은 예제를 풀어 보자.
a : 17 dB까지의 진동 증가를 절대 숫자로 변환하라 (이것은 가속도, 속도 또는 가속도에 적용된다).
17 dB = 20 dB – 3 dB
그러므로 이것은 ![]() = 7.08 의 변화에 해당한다.
= 7.08 의 변화에 해당한다.
b : 진동이 15 dB까지 증가했다. 절대 증가는 얼마인가?
15 dB = 6 dB + 6 dB + 3 dB
이것은 ![]() = 5.63 의 증가에 해당한다.
= 5.63 의 증가에 해당한다.
만일 출력이 입력의 1/10이라면 (장비를 거치고 나면 1/10로 감소된다면), 20 log 1/0.1 = 20 log 10 = 20 dB이 된다. 마찬가지로 100:1의 감소는 40 dB, 1,000:1의 감소는 60 dB에 해당한다.
역학적 범위를 명기하는데 사용되는 20 dB은 장비가 10배까지 다른 신호를 동시에 수용할 수 있다는 것을 의미한다. 40 dB은 100배의 계수와 같다. 일반적으로 명기되는 데이터 수집기나 분석기의 역학적 범위인 72 dB은 약 4,000배의 계수까지 장비가 동시에 다른 신호를 수용할 수 있다는 것을 의미한다. 가스 터빈이나 기어, 그리고 볼베어링과 같은 부품을 가진 기계의 감시나 분석에서는 중요한 상태와 관련된 낮은 수준의 특성들이 Blade-Passing 주파수나 Gear Mesh 주파수에서의 높은 진폭 성분과 자주 혼합되므로 넓은 역학적 범위 용량이 중요하다.
dB 척도는 단지 작은 숫자로 두 개의 량 사이의 비를 표현하는 방법이다. 물론 아직도 비율을 10의 배수가 아닌 dB의 값으로 변환시키는 문제는 남아 있으며 그 역도 또한 마찬가지이다. 로그 함수표나 로그함수를 내장한 계산기가 있으면 dB과 전압비의 변환이 비교적 쉬워지지만 그림 5-1에서 4~5 개의 Key Value를 기억하고 있으면 합당하고 정확한 계산을 할 수 있을 것이다. 그림 5-1이 처음 언뜻 보기에는 약간 복잡하게 보일지도 모르지만 2, 3, 5, 10 그리고 10의 배수의 전압비에 대한 dB 상당량을 빨리 알 수 있게 해 주고 한 단위에서 다른 단위로 변환을 머릿속으로 합당하고 정확하게 할 수 있게 해 줄 것이다. 앞에서 지적한 대로 20 dB은 10배의 전압비를 나타낸다. 다음, 6 dB은 약 2:1의 전압비에 해당하며 10 dB은 약 3:1, 14 dB은 5:1에 해당한다. 전압비와 마찬가지로 50 dB = 40 dB + 10 dB이 된다. 로그 함수에서의 덧셈은 수식에서는 곱셈이 된다는 것을 상기하면 50 dB은 100 (40 dB) × 3 (10 dB), 또는 300의 전압비와 같다는 것을 알 수 있다. 보통 dB에서 전압비로의 변환이 예문에서와 같이 가장 많이 쓰여지며 가장 가까운 20의 배수(20, 40, 60 …)에서 변환하고자 하는 수치를 뺀 다음 전체 전압비를 얻기 위하여 나머지 전압비와 20의 배수에 해당하는 전압비를 곱하여 얻을 수 있다.

그림 5-1 dB과 전압 비의 변환
진동 스펙트럼에서 관심있는 주파수 성분의 진폭이 주된 진동성분 보다도 훨씬 낮은 경우가 종종 있다. 이러한 경우 선형 진폭 척도를 사용하면 기록하기가 곤란하다. 그러므로 일반적으로 대수 척도(Log Scale)가 많이 사용된다. 즉, 대수 눈금은 전체 신호를 보여줄 뿐만 아니라, 높은 수준의 성분이 있는 스펙트럼에서 매우 작은 수준의 성분(볼베어링의 Ball Passing 주파수 성분과 같은)을 강조하여 표시하여 준다.
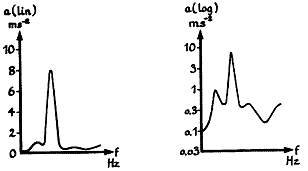
그림 5-2 선형과 대수 척도의 비교
그림5-3은 자동차의 유량계로써 유량계가 선형 척도일 때에는 차에 남아 있는 유량을 판단하기 어려우나 대수 척도라면 눈금의 아래 끝쪽은 탱크에 남아 있는 유량을 더욱 쉽게 알 수 있도록 크게 늘려 나타나게 된다. 대수 눈금은 0이 없으며, 0.1~1까지와 0.05~0.5까지의 간격이 같다.
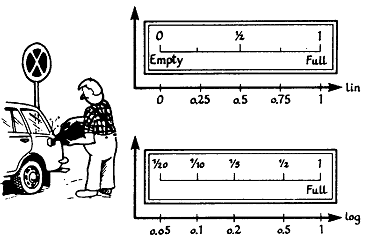
그림 5-3 선형 및 대수 눈금을 가진 유량계 비교
어떠한 척도를 사용할 것인가는 어떤 단위를 사용할 것인가에 달려 있다. 거리와 시간 척도는 선형 척도의 전형적인 예가 되지만 두 수치 사이의 비가 절대치보다 더욱 관심이 있는 경우에는 대수 척도를 사용하는 것이 더욱 좋다. 즉, 우리의 화폐 시스템에서의 동전과 지폐가 갖는 값들을 대수 척도로 그릴 때 근사적으로 인접한 수치들 사이는 거리가 같음을 보여준다.
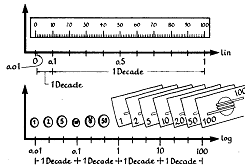
그림 5-4 선형 및 대수 눈금의 화폐 비교
선형과 대수의 주파수 척도는 진동 측정과 관련하여 사용된다. 선형 주파수 척도는 신호에서 조화적으로 연관된 성분들(Harmonics)을 규명하기가 쉽다는 장점을 갖는다. 그러나 대수 스케일은 대역 내에서 훨씬 넓은 주파수 영역을 포함할 수 있으며 10의 지수별 증가당 같은 비율의 중요도를 준다는 장점을 갖는다. 그림 5-5에서 보여지는 신호는 두개의 다른 척도로 그린 기어박스로부터의 진동 신호이다. 이 신호에서 조화적으로 연관된 성분들은 선형 척도에서는 쉽게 규명되어지고, 대수 척도는 아래끝쪽에서는 아주 상세한 반면에 동시에 10배의 넓은 주파수 범위를 포함하여 나타낸다.
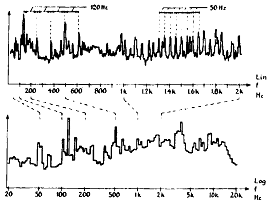
그림 5-5 기어 Box에서의 진동 신호 비교
2. 필터 (Filters)
Filter는 기계 상태의 특수한 특징을 분석하고 감시하기 위하여 복잡한 신호를 간단하게 하는데 사용되는 것으로 한 개의 주파수나 한 그룹의 주파수만 필터를 통과하도록 하고 다른 주파수들은 예측할 수 있는 양상으로 감쇠된다. 라디오 조작자가 Tuner를 필요로 하는 것처럼 진동 분석자는 필터를 필요로 한다.
회전 기계는 마치 많은 방송국을 가지고 있는 국가의 한 지역과도 같다. 각 방송국은 자기 특유의 주파수로 신호를 보내고 있다. 우리가 한 방송국을 청취하고자 하면 Heterodyne Resonance Filter라고도 불리는 Tuner를 특정 주파수 예를 들면 950 kHz에 조정해야 한다. 회전기계의 Oil Whirl 여부를 조사하고자 하면 40~45% 회전속도 주파수 대역을 어떤 형태의 필터를 사용하여 조사해야 한다.
2.1 필터의 種類 (Type of Filters)
기계 분석 장비에서 사용되는 필터는 지정된 주파수를 통과시키거나 차단시키는 성질에 따라 4종류로 대별(그림 5-6)한다.
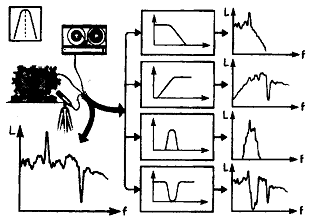
그림 5-6 필터의 종류
2.1.1 低帶堿 通過 필터 (Low Pass Filter)
지정된 주파수 이하의 모든 주파수를 통과시키는 필터로써 가끔 축의 진동변위 신호로부터 축의 긁힌 자국(Scratch)에 의한 진동 성분을 제거하는데 사용된다. FFT 분석에 사용되는 Anti-Aliasing Filter는 매우 경사가 급한(약 100~1,000 dB/Octave) 저대역 통과 필터의 일종이다. API 670은 케이싱 진동 감시기에는 적어도 24 dB/Octave의 경사를 가진 대역통과 필터를 사용할 것을 요구하고 있다.
2.1.2 高帶堿 通過 필터 (High Pass Filter)
지정된 주파수 이상의 모든 주파수를 통과시키는 필터로써 특히 Fan이나 냉각탑, 제지 기계에서 발생되는 복잡한 진동 신호로부터 구조적인 가진을 제거하는데 사용되며, 또한 가속도계로부터의 신호를 변위로 변환시키기 위해 두 번 적분할 때 생기는 잡음이나 구조적 진동을 제거하는데 사용된다.
2.1.3 帶堿 通過 필터 (Band Pass Filter)
지정된 통과 대역에 있는 주파수만 통과시키고, 그 이상과 이하의 주파수는 제거하는 필터이다. 0보다 큰 유한한 Lower Corner 주파수로부터 유한한 Upper Corner 주파수까지에 걸친 단독 전송폭(Single Transmission Band)을 가진 Filter이다. Corner 주파수들은 진폭이 3 dB(0.707)만큼 감쇠되는, 중심주파수의 양쪽 면에서의 주파수들을 의미한다. 중심주파수에서 Signal 진폭은 감쇠하지 않고 위상 선행 또는 지연은 나타나지 않는다.
2.1.4 帶堿 拒否 필터 (Band Reject Filter or Notch Filter)
지정 주파수 범위에 있는 주파수만 제외하고 나머지는 전부 통과시키는 필터이다. Zero보다 큰 유한의 하위 Cutoff 주파수로부터 유한의 상위 Cutoff 주파수의 범위에서 하나의 거부 대역(Rejection Band)을 갖는 Filter이다. 거부 대역 밖의 주파수들은 유지되는 반면, 거부 대역 내의 주파수들은 제거되거나 감쇠 된다. 대역 Filter의 반대.
2.2 帶堿 通過 필터와 帶堿幅 (Bandpass Filter and Bandwidth)
이상적인 대역 통과 필터는 오로지 일정한 대역폭(즉, Bandwidth B=f2-f1)내의 주파수 성분만을 통과시킨다. 그러나 이성적인 필터는 존재하지 않는다. 실제 필터에 있어선, 통과 대역폭 밖의 주파수들도 역시 통과된다(이때, 이 통과 대역폭 밖의 주파수는 감쇠된 형태로 통과한다.) 통과 대역폭으로부터 멀리 있는 주파수 성분일수록 그 감쇠 정도는 커진다. 실제 필터의 대역폭은 2가지 방법 ① -3 dB 대역폭(또는 Half Power Bandwidth) ② 등가 소음 대역폭으로 특징 지워질 수 있다.
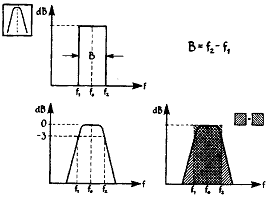
그림 5-7 대역폭의 정의
2.3 帶域 通過필터의 種類 (Types of Band Pass Filter)
2.3.1 一定 帶域 필터 (Constant Bandwidth Filter)
대역폭이 중심중파수에 관계없이 일정하며 대역폭 상하의 차단 주파수(Cut off Frequency)는 필터의 동조에 관계없이 일정(예를 들면 50 cpm 또는 500 cpm)한 필터이다. 일정 대역폭 필터를 사용할 때는 선형 주파수 축을 사용하는데 이는 기계 구조물로부터의 신호가 보통 조화 성분과 측대(Side-Band) 성분을 가져 진동 측정 분석이 용이하기 때문이다.
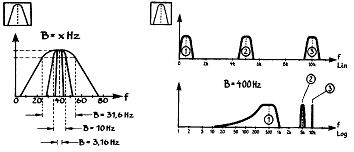
그림 5-8 일정대역 폭 필터의 특성
2.3.2 一定 比率 帶域幅 필터 (Constant Percentage Bandwidth Filter)
일정 대역폭 필터와 혼동을 피하기 위하여 상대적 대역폭 필터(Relative Bandwidth Filter)라는 표현이 더 많이 사용된다. 대역폭이 중심 주파수의 증가에 따라 같이 증가하며 중심 주파수와 상하 차단 주파수의 비율로 정하는 필터이다. 상대적 대역폭 필터를 사용할 때는 대수 주파수 축을 사용하는데 이는 필터가 사람귀 보다 더 근접한 특성을 가져 음향 측정 분석이 용이하기 때문이다. 또한 기계 상태 진단 시에도 상대적 대역폭 필터를 자주 사용하는데 이는 이 필터로 30배의 주파 범위를 쉽게 커버할 수 있기 때문이다.
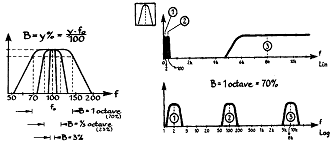
그림 5-9 일정 비율(상대적) 대역폭 필터의 특성
2.4 필터의 感度 (Filter Ability)
여러 가지 다른 주파수 성분을 가지는 신호를 분리하는 능력을 다음 3가지로 특정 지을 수 있다.
① Quality-Factor(Q-Factor) : 상대적 대역폭 필터가 얼마나 좋은가를 나타내 주는데 사용되며 이보다 더 자주 사용되는 용도로는, 공진 구조물의 응답을 표시하는데 사용되는데, 마치 대역 통과 필터처럼 동작하기 때문이다.
② Shape-Factor : 일정 대역폭 필터가 얼마나 좋은가를 지시하는데 사용된다.
③ Octave-Selectivity : 상대적 대역폭 필터가 얼마나 좋은가를 표시하는데 사용된다. Octave란 주파수 축상에서 두 배에 해당한다. 즉, 중심 주파수의 2배 혹은 반등 분을 뜻한다.
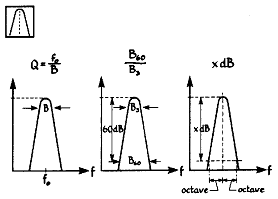
그림 5-10 필터의 능력 표시 방법
2.5 옥타브 (Octave)
Octave는 주파수가 증가되느냐 감소되느냐에 따라 두 배의 주파수가 되느냐 절반의 주파수가 되느냐를 알려주는 또 하나의 상대적인 용어이다. 예를 들면 100 ㎐ 이상에서의 1 Octave는 200 ㎐(12,000 cpm)가 될 것이고, 100 ㎐ 이하에서의 1 Octave는 50 ㎐(6,000 cpm)가 될 것이다. 이와 같이 dB는 진폭 비를 표현하는데 편리한 방법인 반면에 Octave는 주파수비를 표현하는데 편리한 방법이다.
dB/Octave로 지정된 Filter는 만일 차단 주파수가 Filter에 따라 두 배가 되거나 절반이 되면 지정된 값에 따라 출력과 입력의 비가 바뀐다는 것을 의미한다. 만일 20 dB/Octave의 좁은 Bandpass Filter의 중심이 100 ㎐이고 1 볼트의 가변 주파수가 입력되면 이상적인 Filter의 출력은 50 ㎐(Filter의 중심주파수 이하로 1 Octave)에서 0.1 볼트, 100 ㎐에서 1.0볼트, 200 ㎐(Filter의 중심주파수 이상으로 1 Octave)에서 0.1 볼트가 될 것이다. 100 ㎐가 중심주파수인 Filter에 동일한 입력과 40 dB/Octave가 주어지면 50 ㎐에서는 0.01 볼트의 출력을, 100 ㎐에서는 1.0 볼트를, 200 ㎐ 에서는 0.01 볼트의 출력을 얻게 될 것이다.
2.6 Filter의 變換特性-Rolloff (Filter Transfer Characteristics-Rolloff)
Filter는 Passband 밖에 있는 모든 주파수를 즉시 차단하는 것이 아니고 dB/Octave로 정의된 경사 선을 따라 주파수에서의 응답을 감소시킬 것이다. 이러한 설명은 Filter의 두 번째 Octave와 그 밖의 영역에서는 옳으나 첫 번째 Octave 내에서는 절대적으로 옳은 것은 아니다. 그림 5-11에서 보여준 것과 같이 단일 이득 영역(Filter의 통과 대역)과 감쇠 영역 (Filter의 변두리) 사이에 변환점이 있다. 이상적으로는 이 변환점은 날카로운 모서리이어야 하나 실제로는 증가하는 경사도를 가진 곡선이다. Filter가 가능한 한 빨리 감쇠를 시작하기 위해서는 요구되는 통과 대역 내에서 감쇠가 시작되어야 한다. 이러한 감쇠점은 3%나 3 dB점으로 정해진다. 이러한 지정은 대역의 모서리 부분에서의 Filter 출력은 입력과 비교하여 3%(0.97)이나 3 dB(1/1.41 = 0.707)까지 감소됨을 의미한다.
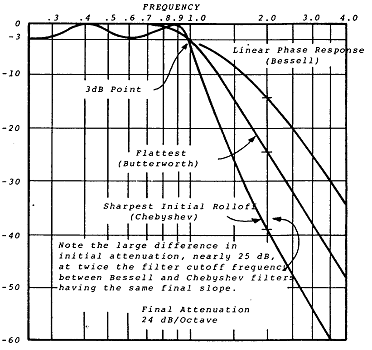
그림 5-11 Filter의 응답
Filter는 특별한 초기 Rolloff 특징을 표현하기 위하여 명명될 수 있다. 그림 5-11에 보여지는 여러 Filter 중에서 Butterworth Filter는 대역 내에서 가장 균일한 응답 특성을 가지고 있어서 그것의 느린 초기 Rolloff에도 불구하고 기계 감시에 종종 사용된다.
Filter는 경사진 가장자리를 가지고 있고 그 출력은 지정된 Filter 끝지점의 약 1/2 Octave내에 위치된 강한 성분으로부터 큰 영향을 받는다는 것을 기억하는 것이 중요하다. FFT 분석기에서의 Filter 기울기에 대한 지식은 분석기에 의한 기본적인 분석보다도 더욱 정확하게 주파수를 측정, 계산할 수 있는 기초적인 능력을 제공한다.
Filter의 또 하나의 다른 변환 특성을 간단하게 언급한다. 즉, 신호가 Filter 끝지점을 지나면서 180°의 위상각의 변화가 발생한다는 것이다. 기계 분석에 사용되는 많은 장비들이 어떤 형식으로 위상각을 보상하고 있지만 기계 분석 기구의 사용자들은 위상각을 측정할 때 잠재적인 부정확성을 알고 있어야만 한다.
문제를 일으킬 수 있는 또 다른 핵심은 제한된 주파수 응답을 가지고 있는 기록 장비가 기준 위상각 펄스와 같은 비정현파적인 신호와 연결될 때 발생되는 유효한 Filtering이다. 이러한 극단적인 예에서는 신호의 기본이 충분히 기록 장비의 주파수 범위 내에 있을지라도 실제로 신호가 왜곡되는 것이다 (그림 5-12).
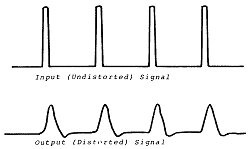
그림 5-12 부적당한 고주파수 응답에 의한 왜곡
2.7 Tracking Filter
Tracking Filter는 외부의 기준 신호(보통 축의 회전 주파수에 동기된 신호)와 맞춰지는 중심주파수를 가진 Bandpass Filter이다. 그러므로 Tracking Filter는 축의 회전 주파수를 추종하고 회전 주파수에 고정된다. 일반적으로 어떠한 동기 배수의 회전 주파수도 추적할 수 있도록 제어장치가 갖추어진다.
Tracking Filter는 Balancing이나 기동 정지 시의 진폭 응답, 위상각의 측정 등에 널리 사용된다. 대부분의 FFT 분석기는 Tracking 기능을 가지고 있다. 사실상 대부분의 장비가 디지털로 Tracking과 Filtering 기능을 수행하지만 기본 원리와 용어들은 아날로그와 디지털 설비에 모두 적용한다.
추적율(Tracking Rate)은 급작스럽게 주어지는 입력에 대해 Filter 출력이 응답하는데 필요한 시간에 좌우된다. 이론적이기는 하지만 추적율은 입력과 출력사이에 지정된 정확성을 유지하면서 Filter가 주어진 대역을 가지고 중심주파수의 변화를 추종할 수 있는 최대 비율을 나타낸다. 실제 용어에서는 추적율이란 Tracking Filter가 정확하게 추종될 수 있는 최대 속도 변화율을 나타낸다.
Tracking Filter가 변화하는 중심주파수를 추종할 수 있는 비율은 ㎐로 나타낸 주파수 대역폭의 제곱에 비례한다. 예를 들어 1 ㎐/sec (60 cpm/sec)는 1 ㎐(60 cpm)의 Filter 주파수 대역폭에 대한 최대 추적율이다. Filter의 주파수 대역폭을 10 ㎐(600 cpm)까지 증가시키면 최대 추적율은 약 100 ㎐/sec (6,000 cpm/sec)까지 증가된다.
앞의 설명은 개략적인 것에 지나지 않지만 기계 감시에서 Filter를 사용할 때 고려하여야 할 물리적인 제약 조건(Constraint)을 설명하고 있다.
2.8 넓은 周波數 領域을 어떻게 포함할 것인가? (How to Cover a Wide Frequency Range?)
협대역 필터를 이용해 넓은 주파수 영역을 분석하기 위해선 그 관심 주파수 전영역을 포함하는 여러 개의 필터를 갖추어야 한다. 이를 위해선 원리적으로 두개의 다른 방법이 있다.
① 하나의 필터로 주파수 영역을 소인해 가는 방법 (Continuous Filter)
② 여러 개의 필터를 그들끼리 교번시켜 주파수 영역을 다루는 방법 (Contiguous Filter)
해석 결과가 꽤 틀리게 보이지만 Contiguous Filter(인접 필터)와 Continuous Filter(연속 필터) 사이에는 원리적으로 전혀 차이가 없다. 즉, 두 결과들은 잘 일치한다.
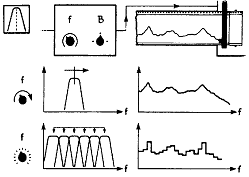
그림 5-13 협대역 필터로 넓은 영역을 분석하는 방법
2.9 帶域幅이 다른 경우의 차이점 (Results With Different Bandwidth)
서로 다른 대역폭의 필터를 사용하여 측정해 보면 결과가 서로 약간 다르다. 여기서 결과란 분석되는 신호에서의 에너지 측정량을 말한다. 협대역 필터를 갖고 해석하게 되면, 광대역 필터로 분석한 것보다 낮은 값을 얻게 된다. 왜냐하면, 협대역 필터에는 작은 에너지가 통과하기 때문이다.
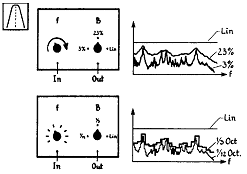
그림 5-14 대역폭이 다른 필터를 사용했을 경우의 출력 변화
2.10 필터의 應答時間과 BT (Resonance Time of a Filter and BT)
그림 5-15의 예는 갑자기 가해진 정현파에 대한 필터의 응답을 나타내 주고 있다. 그림에서와 같이 필터의 출력은 그 값이 점차 증가하여 일정한 응답 시간이 지난 후에 최고치에 도달하는데 약 1/대역폭(B)이 된다. 다시 말하면, 대역폭과 응답 시간의 곱은(BTR)은 1이 된다. 따라서 필터에겐 항상 평균(Averaging) 하기 전에 응답에 대한 시간이 주어져야 한다.
BTR값은 항상 거의 1이므로 협대역 분석에서는 광대역 분석에서 보다 비교적 긴 분석 시간이 필요하게 된다. 이것은 항상 주파수 분석을 행할 때 기억해 두어야 할 일반적인 규칙이다.
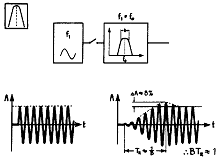
그림 5-15 필터의 응답시간
3. 적분 (Integration)
적분은 가속도를 속도로, 속도를 변위로 환산할 때 이용하는 수학적 처리 과정이다. 임의의 가속도로부터 속도와 변위를 구하려면 가속도 스펙트럼 성분에 단위 주파수 변화분의 역(한번 적분)과 제곱의 역(두 번 적분)을 곱함으로써 얻을 수 있으며, 곱하고자하는 주파수 변화분의 단위는 2배, 4배 10배 등으로 선택하는 데 따라 달라진다.
그림 5-16은 최고치가 1g인 일정한 가속도에 대하여, 속도와 변위를 구한 수학적 처리(적분) 결과를 보여주고 있다.
이러한 정보는 일반적으로 그래프로 나타내고 있지만, 몇 개의 관심있는 부분의 스펙트럼에 대한 정보는 그래프보다 표에서 훨씬 더 잘 나타낼 수 있다. 즉 주파수가 2배 증가하면, 속도와 변위는 각각 1/2과 1/4로 감소됨을 쉽게 알 수 있다.
전술한 데시벨(dB) 개념에서, 6 dB과 12 dB의 감속비에 대하여 고찰해 보면, 한번 적분과 두 번 적분은 각각의 기울기가 6 dB/Octave와 12 dB/Octave인 직선상에 위치한 한 요소와 주어진 주파수의 곱임을 알 수 있다.
| Frequency, ㎐ | Velocity, in/sec Peak | Ratio | Displacement, mils Peak-to-Peak | Ratio |
| 12.5 | 4.92 | 2.0 | 125 | – |
| 25 | 2.45 | 2.0 | 31.3 | 4.0 |
| 50 | 1.23 | 2.0 | 7.8 | 4.0 |
| 61.4 | 1.0 | – | 5.2 | – |
| 100 | 0.6 | 2.0 | 1.96 | 4.0 |
| 140 | 0.44 | – | 1.0 | – |
| 200 | 0.31 | 2.0 | 0.49 | 4.0 |
| 400 | 0.15 | 2.0 | 0.12 | 4.0 |
그림 5-16 일정한 가속도 1g에 대한 속도와 변위값
그림 5-16은 또한 Zero 입출력비나 영국 단위계에서의 1g와 속도 1 in/sec(61.4 ㎐)와 같아지는 교차점과 1g가 변위 1 mil(140 ㎐)과 같아지는 교차점을 보여준다. 미터 단위계에서 가속도와 속도, 가속도와 변위가 같아지는 교차점은 각각 1,560 ㎐(㎜/s), 705 ㎐(㎛)이다.
또한 주파수가 감소함에 따라 1g의 가속도에서 변위값이 급격히 증가하는 것을 주목하라. 이러한 증가는 변위가 가속도와 주파수 제곱의 역수와의 곱이란 관계 때문이며, 매우 낮은 주파수에서 두 번 적분할 때 문제를 발생시킬 수 있다. 더 자세히 설명하기 위하여 주파수를 20 Octave 더 감소시켜 3.125 ㎐까지 감소시켜 보자. 이점에서 1g의 가속도에 해당하는 변위는 약 2.0 in, 또는 2,000 mils (51 ㎜)에 달한다. 사람들이 의문을 가지는 것과 마찬가지로 적분 과정이 Zero 주파수까지 계속될 수 없는데 이것은 무한한 증폭을 요구하기 때문이다. 낮은 주파수대에서는 이러한 증폭 문제 때문에 적분기는 미리 설정한 주파수 이하의 신호를 감쇠 시키는 High-Pass Filter를 갖추어야 한다. 가속도 변환기를 사용하는 기계에서 두 번 적분하기 위한 필요 조건은 주파수를 더 낮추어야 하는 것이기 때문에, 실제로 기계 상태를 지시하는 것이 아닌 구조적 진동이나 지진의 운동에 의해 발생하는 신호가 신호 변환기에서 검출되고, 적분되는 과정에서 크게 증폭되는 저주파 신호를 제거하기 위해서는 High Pass Filter의 대역폭은 아주 정확하여야 한다.
이것을 설명하기 위해서 1 ㎐(60 cpm)에서 약 100 mils(2,450 ㎛)의 구조적 진동을 가지고 있는 Fan과 같은 기계에서 10 ㎐(600 cpm)에서 10 mils(254 ㎛)정도의 진동 측정치를 살펴보자. 원하는 측정치를 얻어내고 잡음(Noise)을 제거하기 위하여, 만일 잡음을 측정하고자하는 신호 성분의 10% 이하까지 감쇠 시켜야 한다면, 입력되는 신호는 10에서 5 ㎐ 사이인 1 Octave에서 계수 100까지 감쇠 되어야만 한다. 이렇게 감쇠 시키려면 40 dB/Octave의 Filter가 필요하다. 그러나 이렇게 기울기가 급한 필터는 구하기가 쉽지 않다. 보통의 상황은 기술한 것만큼 심각하지는 않지만 매우 낮은 주파수까지 두 번 적분할 때 생기는 잠재적인 문제에 대하여 알고 있어야 한다. 이러한 예문들은 낮은 주파수에서 진동 신호를 적분할 때 일반적으로 관측되는 “Ski Slope” 모양의 원인을 설명하고 있다.
이러한 문제가 생기는데도 도대체 왜 진동 신호를 적분하는 것일까? 가장 중요한 것은 적분을 함으로써 복잡한 진동 신호 중에서 강조하고 싶은 부분을 이동시킬 수가 있다는 것이다. 주파수 제곱의 관계 때문에 높은 주파수에서는 가속도 신호가 두드러질 것이다. Balancing이나 축정렬과 같은 일반적인 상태를 평가하기 위하여 운전 속도 근방으로 주파수를 낮추어 강조하는 부분을 이동시키기 위해서는 가속도 신호를 속도값으로 적분하는 것이 타당하다고 할 수 있다 (그림 5-17). 덧붙여 말하면 케이싱 진동을 지진계식 감지기로 측정할 때 가장 정확한 상태 지시계로 일반적으로 인정되는 수용 기준은 약 10 ㎐에서 1,000 ㎐ (600 cpm에서 60 kcpm)까지 일정한 속도값으로서 표현되는 것이어야 한다는 것이다.
어떤 시스템에서는 냉각 Fan과 같이 저속 기계를 감시할 때 변위값을 얻기 위하여 두 번 적분되어야 하는 가속도 변환기로 사용할 필요가 있는 경우가 있다. 경험상으로 비추어 볼 때 낮은 주파수의 구조적 가진력이 거의 항상 문제를 생기게 하기 때문에 이것은 부적합하며 속도값이 더욱 안정된 측정값을 제공하며 더 양호한 상태 지시를 할 수 있다.
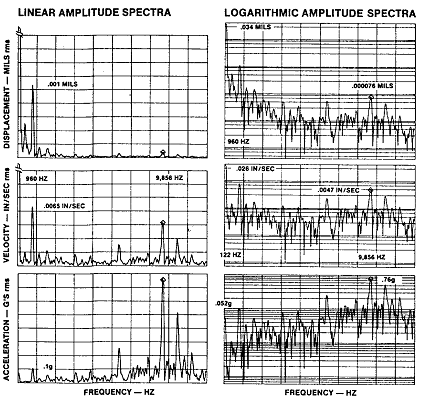
그림 5-17 속도와 변위로 적분된 가속도 신호. 가속도가 스펙트럼의 고주파수 부분을,
속도는 중간 주파수 부분을, 변위는 낮은 주파수 부분을 얼마만큼 강조하는가를 주목하라
4. AC에서 DC로의 변환 (AC to DC Conversion)
DC(직류)는 크기와 방향이 일정한 것을 말한다. 비접촉식 진동 측정에서 Pick-up의 Gap에 따른 Gap Voltage는 DC에 속한다.
AC(교류)는 시간에 따라 크기와 방향이 주기적으로 바뀐다. 진동 신호도 역시 시간에 따라 크기와 방향이 주기적으로 바뀌므로 AC에 속한다. 진동진폭을 수치로 표시할 때는 진동신호 AC를 DC로 변환이 필요하다. AC에는 모양에 따라 여러 파형이 있으며 그의 크기 AC를 비례하는 DC값으로 나타내는 방법은 최대치(Peak to Peak), 평균치(Average), 실효치(RMS)가 있다. 파형에 따라 같은 크기의 최대치를 갖는 AC라 할지라도 평균치 및 실효치와는 다를 수 있다.
최대치, 평균치, 실효치에 대해 정의하면 다음과 같다.
• 최대치(Peak to Peak)
순시치 가운데 가장 큰 값을 최대치라 하며 AC파형 주기중 반드시 하나가 존재한다. 진동 신호에서는 최대 왕복 행정을 의미한다.
• 평균치(Average)
AC 파형의 순시치를 평균한 것이다. 정현파인 경우 1주기를 평균하면 + 반주기와 – 반주기가 면적이 같이 0이 되므로, 반주기 순시치의 면적합을 다음과 같이 구한다.

• 실효치(RMS)
AC에서 가장 잘 사용되는 방법이 실효치이다. 실효치는 에너지 차원에서 DC와 동일한 크기의 AC를 의미한다. 그러므로 실효치를 사용하면 여러 가지의 계산에서 DC와 같게 취급된다. 정현파인 경우 다음 식에서와 같이 교류의 실효치(Erms)는 순시치 또는 최대치(Em)의 2승의 평균의 평방근이다.
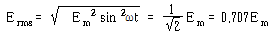
DC와 AC 성분은 결합될 수 있으며 결합된 모양의 파형은 다음 그림과 같다. 이 결합된 성분에서 DC 성분만 제거시키면 순수 AC만 남게 된다.
예를 들면, 비접촉식 진동 측정시스템에서는 Pick-up을 여자 시키기 위해 일정한 크기의 DC 전압을 공급하는데, 이 전압이 Gap 전압이며, Pick-up과 축간의 간격(Gap)에 따라 변하게 된다. 정지중 이거나 진동이 전혀 없는 기계에서는 Pick-up과 축간의 간격은 일정하므로 Gap 전압은 초기에 공급한 일정한 크기의 DC 전압으로 나타난다. 그러나 운전중인 기계에서 진동이 발생하면, Pick-up과 축간의 Gap은 연속적으로 변하고, Gap 전압 또한 끊임없이 변하게 된다. 이때 Gap 전압의 파형은 진동에 의한 Gap 전압 변화분인 AC 성분과 초기에 공급한 DC성분이 결합되어 그림 5-18a와 같은 파형을 취한다.
실제 진동성분만을 알려고 할 때는 AC와 DC가 결합된 파형에서 초기에 공급한 DC성분을 제거하고, 기계의 순수한 진동성분인 AC 만을 취하면 된다.
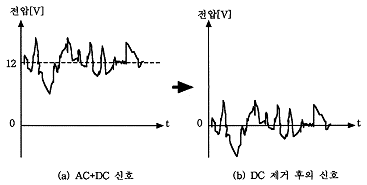
그림 5-18 순수한 진동 신호의 선별 개요
실제 Peak-to-Peak의 검출은 진동 신호의 양쪽 끝점의 최대 왕복 행정을 취하게 된다. 실제 Peak-to-Peak값의 검출은 비접촉식 변환기로 감지하는 축 변위 측정기를 사용하여야 한다. 이 경우에 측정치는 베어링과 Seal의 간극과 같은 물리적인 제약조건과 직접적으로 비교할 수 있는 실제적인 총 움직임을 나타내야 한다. Peak-to-Peak값의 검출은 회전축의 긁힌 흠집이나 표면 결함과 같은 것에 매우 민감하다는 사실에 주의하여야 한다.
RMS값의 검출은 축변위 측정에 절대로 사용되어서는 안된다. 이것은 Rub나 충격과 같은 상황에 의해 생기는 잠재적인 손상 위험성이 있는 축의 움직임에 민감하지 못하다. 이와 같이 RMS는 동력학적인 실제 움직임에 대한 양상을 정확하게 표현하지 못한다.
진동 신호에서 Peak, 즉 Zero to Peak의 검출은 Zero에서 양(+)의 최대 행정과 같고, 짧은 시간 동안 지속되는 Peak값을 포함한다. 만일 진동 신호가 Zero점을 중심으로 대칭이라면 Peak값은 실제 Peak-to-Peak값의 절반이 될 것이다.
Peak-to-Peak의 검출과 같이 Zero-to-Peak값의 검출도 높은 진폭과 기어 및 볼베어링의 결함의 초기 징후에 민감하다. Peak값의 검출은 볼베어링의 Pitting과 같은 결함을 생기게 하는 충격의 징후를 가장 초기에 감지하는 속도와 가속도 측정에 효과적으로 사용된다.
진동 신호에서 Root Mean Square (RMS) 검출은 시간영역의 진동 신호 파형 면적(제곱한 값의 제곱근)에 비례하는 시간-평균 진폭을 만들어 낸다. 진동 신호의 RMS로의 검출은 짧은 시간 동안 지속되는 Peak값의 응답을 감소시킨다. 사실상 RMS의 검출은 고 주파수의 Peak값을 포함하고 있는 신호를 평균을 내고 간략하게 하여 Unbalance나 Misalignment와 같은 문제를 암시하는 조화 운동을 보다 더 정형적으로 만든다.
입력이 순수한 정현파라면 RMS 진폭은 각각 1.414나 2.828을 곱하여 Peak나 Peak-to-Peak로 변환될 수 있다. 이러한 관계는 입력이 전기 신호 발생기로부터 얻어지거나 회전 주파수에서 주로 정현파적인 진동을 갖는 전동기나 Fan, 펌프와 같은 간단한 기계일 경우에 정확한 값이 된다.
만일 입력 신호가 정현파와 비정현파 성분이 혼합되어 있다면 RMS와 Peak의 관계는 훨씬 더 복잡해지게 된다. 비정현파적인 충격형 Peak값(볼베어링의 결함이 한가지 원인임)을 가지고 있는 기계에서는 실제 Peak값은 동시에 측정한 RMS 값에 1.414를 곱하여 얻어낸 값보다는 훨씬 더 클 것이다. 그림 5-19의 아랫부분은 극단적인 예를 보여주고 있으며 이 예에서 Peak 감지기로 측정된 Peak값은 RMS에 1.414를 곱하여 얻어낸 진폭보다 분명히 훨씬 더 크다.
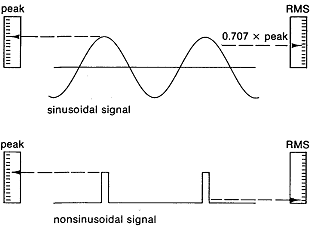
그림 5-19 정현파와 비정현파 신호에 대한 Peak와 RMS 값의 비교
Severity Chart와 케이싱 부착용 속도 및 가속도 변환기에 사용하기 위하여 제작되는 많은 진동 계측기가 측정한 RMS값에 1.414를 곱한 값을 Peak값이라고 잘못 적용하고 있다.
실제 Peak값을 취하느냐 RMS값을 취하느냐 하는 실질적인 문제는 고주파수의 충격형 가진력에 민감하게 할 것인가 또는 Unbalance나 Misalignment 등의 정현파적인 증상에 주로 초점을 맞출 것인가에 좌우된다. RMS의 검출은 손상이 주로 에너지의 함수로 나타나는 곳에서 Unbalance나 Misalignment와 같은 일반적인 문제의 Severity를 평가하거나 확인하기 위하여 케이싱 진동을 측정하는데 있어 최상의 측정치라는 것이 경험에 의하여 명백히 증명되었다.
고주파수의 충격에 대하여 감도가 민감하기 때문에 실제 Peak값의 검출은 볼베어링과 기어의 결함을 초기에 경고해 준다.
실제의 Peak-to-Peak값은 축진동의 감시 및 분석에 사용되어야 한다.
포괄적인 예지 감시 프로그램은 세 가지 방법을 모두 사용하여야 하며, RMS 속도값은 케이싱 진동으로 Unbalance나 Misalignment와 같은 상태를 평가하는데 사용되어야 한다. 볼베어링이나 기어의 결함을 조기에 경고하기 위해서는 Peak 가속도를, 유막 베어링을 사용하는 대형 기계의 상태를 평가하는데는 Peak-to-Peak 축변위를 사용하여야 한다.
그 외에 기계 분석자가 알아두어야 할 한가지 요점은 AC to DC 변환기, 특히 매우 낮은 주파수에서 운전되도록 설계된 Peak 감지기에는 반드시 응답 시간이나 지연이 있어야 한다는 것이다. AC-to-DC 변환기가 신호를 감지하면 그 신호가 반복될 때까지 한 사이클을 기다려야 한다. 그림 5-19의 아랫부분에서 높은 진폭이지만 짧은 시간 동안 지속되는 펄스와 같은 입력이 주어지는 Peak 감지기의 예로 되돌아가 보면, 한 사이클이 이루어지는 동안 감지기에 주어지는 입력의 대부분은 Zero이다. 만일 감지기가 적당한 정확성을 가진 감지기로 실제 Peak 값을 측정하고자 한다면 소멸되는 비율을 억제하는 매우 큰 시간 상수를 가져야만 한다. 그렇게 되면 신호가 갑자기 제거될 때 출력은 천천히 응답하고 곧바로 Zero로 떨어지지 않고 감지기의 시간 상수에 의해 결정된 비율로 천천히 소멸될 것이다. Sampling과 같은 다른 요인들은 전형적인 분석기에 더 큰 영향을 주겠지만 전기 전동기로부터 전원을 제거할 때의 진폭 변화와 같은 아주 순간적인 것의 실제 양상은 대부분의 표시화면이 제공하지 못한다는 것을 알고 있어야만 한다. 실제로 무엇이 일어나고 있는가를 알기 위해서는 신속하게 응답하는 장비를 사용하여야 한다.
5 자료의 질을 향상시키기 위한 신호처리 (Signal Processing for Data Enhancement)
5.1 平均化 (Averaging)
FFT분석기는 측정된 신호를 분석하는데 정확성을 기하기 위하여 평균화 기능을 이용하고 있다. 이 평균화 기법은 신호를 주파수 영역에서 처리하는 주파수 영역 평균화와 시간영역에서 처리하는 동기 시간 평균 평균화 두 가지가 있으며, 일반적으로 기계의 운전 상태 감시나 분석에는 주파수 영역 평균화 기법이 널리 이용되고 있다.
5.1.1 周波數 領域 平均化 (Frequency Domain Averaging)
주파수영역의 평균화는 일련의 동일한 스펙트럼을 미리 정해 놓은 수만큼의 스펙트럼을 평균화하는 과정이다(정상상태의 기계분석에 적당한 스펙트럼 수는 6~8개임). 주파수영역의 평균화는 기준입력이 필요 없지만, 신호에 따라 많은 평균화 횟수가 요구되거나, 속도가 변하는 경우에는 기준입력, 즉 크기, 주파수 등이 규정화된 기준 스펙트럼을 이용하는 것이 바람직하다. 이러한 두 가지 상황하에서는 평균화 과정이 진행되는 동안에 속도가 미세하게 변하여도 Smearing 현상(회전주파수 및 그에 관련된 성분이 다수 복합된 선으로 나타나는 현상)이 일어나, 진폭측정의 정확성이 떨어질 수 있다. 그리고 주파수 영역 평균화는 스펙트럼에 실리는 미소한 잡음신호를 완전히 제거는 못하지만 실효치 값으로 크게 감소시킨다.
주파수 영역에서의 규정화된 위상 기준 평균화는 장시간에 걸친 경향 감시에 필요한 위상의 정확한 측정을 가능하게 하지만, 신호의 위상 측정 자체가 크기 측정에 비하여 측정자료의 불확실성이 더 높기 때문에 크기 측정에서와 같이 동일한 정확도를 얻기 위해서는 평균화 횟수를 더 늘여야 한다. 이러한 문제를 극복하기 위해서, 위상 측정치가 안정된 값에 도달하였을 때, 인위적으로 평균화 과정을 중지시키는 연속 평균화 기법을 추천하는 사람도 있다.
5.1.2 同期 時間 平均化 (Synchronous Time Averaging)
동기 시간 평균화는 위상을 기준으로 일련의 동기 시간 신호를 평균화하고, 이 결과가 주파수 영역으로 변환됨으로써 과정이 완성된다. 동기 시간 평균화를 위해서는 분석 대상인 축과 동기 상태인 Reference Trigger, 많은 평균화 횟수, 그리고 100% 신호처리(0 Overlap)가 필요하다.
동기 시간 평균화는 신호 처리에 있어서 동기 성분은 크게 강화되고 비동기 성분과 잡음 신호는 “0”에 가깝게 감소되어 분석 자료의 질을 향상시킬 수 있다. 즉 동기 시간 평균화법은 다음과 같은 이점을 가지고 있다.
• 발란싱을 위한 위상 정확도를 향상.
• 인접한 기계로부터의 가진과 같은 외부 가진의 영향을 제거.
• 제지 기계의 특정 롤러 또는 복잡한 기어내의 특정 축과 같은 특정기계 요소를 분리.
• 잡음 신호와/혹은 크기가 큰 비동기 신호의 성분이 포함된 신호로부터 매우 낮은 크기 성분은 추출.
5.2 Envelope Detection
Envelope Detection에서는 크기가 적은 신호, 고 증폭에 의한 결함 신호의 특성 및 저주파 신호를 추출해내기 위한 3단계 과정을 설명한다. 이 방법은 결함을 더 빨리 그리고 훨씬 신뢰성 있게 알아내는 방법을 제공하며, 대체로 주파수가 낮고 진폭이 작은 반복적인 사건(톱니바퀴에서 손상된 이빨이 맞물리거나 베어링에서 깨어진 볼이나 롤러가 Race를 치는 것과 같은 경우)의 신호를 고주파 신호로 변조시키는 기어와 구름요소 베어링의 상태 분석에 널리 이용된다 (그림 5-20a).
Envelope Detection 방법은 반복성이 뛰어나고, 성능이 우수하여 신호 변환에 일관성이 있는 신호변환기를 장착함으로써 최대의 이점을 얻을 수 있다. 바닥이 자성을 지니고 있는 가속도계는 기계표면의 평평한 부위에 댐핑이 없는 접착제를 이용하여 튼튼하게 취부하면 좋은 측정 결과를 얻을 수 있다는 것이 밝혀졌다.
Envelope Detection은 측정된 가속도 신호로부터 저주파 신호를 제거하기 위한 여과 과정으로부터 시작된다. 원하는 신호를 얻기 위한 여과 방법은 취급하는 사람들에 따라 의견이 다를 수 있다. 즉, 여과된 고주파 신호로부터 기계상태와 그에 관련된 많은 정보를 얻을 수 있다고 생각하여 고주파 필터를 주장하는 사람과 특정한 주파수 신호에 관심의 초점을 맞출 수 있도록 특정 주파수 영역만의 신호만을 선택할 수 있는 특정 주파수 대역 필터가 유리하다고 주장하는 사람이 있다.
어느 경우나 회전 주파수대의 신호, 낮은 차수의 배수주파수 신호 및 베어링 결함 주파수 신호 등을 제거할 수 있도록 저주파 차단 주파수 범위를 설정하여야 한다. 어떤 계측기 제작자는 회전 주파수의 10배를 최소 저주파수 차단 범위로 추천한다.
특정 주파수대역 선택 방법을 이용하는 한 측정장치 제작자는 기계의 회전주파수를 기준으로 하여 1200 rpm이하의 저속 기계에 대한 주파수 선택 범위는 50 ㎐에서 1000 ㎐까지, 3600 rpm 에 이르는 고속 기계에 대해서는 500 ㎐에서 10 kHz의 주파수 대역을 선택하였다. 반면에 어떤 제작자는 신호의 재현성을 최대로 높이기 위하여 주파수 대역의 상한을 10 kHz까지로 제한할 것을 추천하고, 또 다른 제작자는 주파수 상한을 50 kHz까지 더 높임으로써 얻을 수 있는 이점을 주장하고 있다. 필터의 대역폭 내에 베어링의 고유 진동 주파수가 포함되면 결함신호는 공진 증폭에 의해 실제보다 높아진다고 한다.
같은 목적을 얻기 위해 어떤 방법이 가장 좋은 방법인가에 대해서는 너무나 많은 다른 관점이 있기 때문에 필터의 목적을 아는 것이 매우 중요하다. Envelope Detection에 앞서 신호를 여과하는 것은 오로지 미소한 신호의 특징을 최대로 향상시키기 위한 것이다.
일단 필터의 구성방법이 결정되면 그후에 이루어지는 측정에도 동일한 필터구성을 사용해야 한다. 신호가 여과되고 정형된 후에는 Envelope Detection과정을 거치게 된다. Envelope Detection에 의해 검출된 신호는 몇 단계의 필터를 거치면서 그림 5-20b와 같이 작은 신호가 Envelope형태로 변조된 출력을 얻게 된다.
시간영역에 표시된 Envelope는 펄스 반복주파수, 피크 값, 평균화 값 그리고 Envelope을 만들어 내는 주기에 대한 정보를 포함하고 있다. Envelope에서 감지된 신호는 진폭 및 주파수 내용에 대한 보다 정교한 분석을 위해, FFT로 처리, 분석되어, 그 결과는 우리 눈에 익숙한 진폭 대 주파수 형태로 표시된다.
이 Envelope Detection에서 중요한 것은 우리가 신호에서 측정, 처리하는 충격적인 특징만을 선택적으로 통과시킨다는 것이다. 만약 신호의 충격적인 특징이 없으면, 나타나는 스펙트럼에는 문제를 나타내는 성분이 빠져있는 것이다. 그러므로 Envelope에서 감지된 스펙트럼 내에 어떤 성분의 출현이나 존재는 결함을 나타내는 것이다.
그림 5-20a Envelope Detection하기 전의 원래 신호
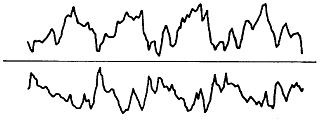
그림 5-20b 시간영역에서 Envelope Detect된 Output
5.3 周波數 復調 (Frequency Demodulation)
Dynamic 신호는 여러 가지 방법으로 변환될 수 있다. 만일 Dynamic 신호가 진폭 변조되었다면, Envelope Detection 기술은 변조에 의해 정보를 추출할 것이다. 평균화 값을 기준으로한 주파수의 순간 변화로서 정의되는 주파수 또는 위상 변조는 기어 이빨 간격이 잘못되었거나 기어 이빨이 불균일하게 닳았거나 또는 비틀림 진동과 같은 현상에서 기인한 운전 기계에 의해서 발생된 진동 신호에서 역시 발생될 수 있다. 그림 5-21에 나타난 것처럼 주파수 변조된 신호의 평균화 값은 1 회전마다 발생된 사건의 횟수를 초당 회전수와 곱하면 계산해 낼 수 있다. 만일 불균등한 이빨 간격이나 비틀림 진동이 존재한다면 순간 주파수는 기계가 신호를 발생시키는 Mechanism에 따라 결정되는 율에 따른 평균화 값 전․후로 변할 것이다. 그러므로 비틀림 진동이나 이빨 간격이 잘못된 것과 같은 상황은 평균 주파수에서의 비율 혹은 주파수를 측정함으로 해서 확인될 수 있다.
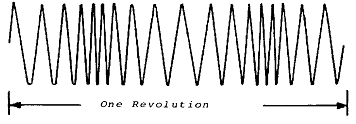
그림 5-21 주파수가 복조된 신호
이 그림에서는 회전수당 18배(주파수)의 반송파가 회전수당 2배로 변조된 것을 보여준다.
보통, 회전수당 40~수백 배에 달하는 아주 높은 주파수를 반송파로 사용한다.
실제로 주파수가 변조된 것으로 의심이 가는 신호는 주파수 복조기를 통과시킨다. FM 라디오를 방송국의 주파수에 맞추는 것과 똑같이 주파수 복조기를 점검하고자 하는 신호에 주파수를 맞춘다. 주파수 복조기내에서 평균화 값과 비교한 주파수 편차의 크기는 진폭으로 변환되고, 이것의 반복율은 주파수로 변환된다. 그러므로 주파수 복조기의 출력은 순간적인 주파수 편차에 비례하는 순간의 진폭과, 편차가 발생되는 비율에 비례하는 주파수를 가진 시간영역 신호이다. 이 신호는 시간영역에서 표시되거나 분석될 수 있다; 그러나, 만일 주파수 복조된 신호가 FFT 분석기를 이용하여 주파수 영역으로 변환되어지고 또 재래식 진폭 대 주파수 형태로 표시되어진다면 분석 작업은 더욱 효과적으로 성취되어질 수 있다.
주파수 복조와 분석을 위한 이런 절차는 비틀림 분석에도 종종 이용된다. 이러한 유형의 분석에서는, 이빨 사이의 간격이 정교하게 제작된 기어를 축상에 설치하여 측정한다. 비접촉식 광학 Pickup, Magnetic Pickup 또는 Eddy-current 형식의 Pickup은 분할된 표면을 관측하여 각 분할된 조각이 통과할 때에 Pulse를 발생시키도록 설치된다. 분할된 조각들은 매우 정밀한 허용오차 내에서 동일하게 간격이 떨어져 있기 때문에, 어떠한 비틀림 진동이라도 표면 통과 주파수(즉, 분할된 조각 × 축속도)의 주파수 변조를 발생시킬 것이다.
5.4 켑스트럼 分析 (Cepstrum Analysis)
그 명칭과 용어가 당황스럽지만 Cepstrum은 단순하게 Spectrum의 Spectrum이다. 그래서 기본 주파수와 이것들의 Harmonic 급수들(Series)은 한가지 성분으로 축소된다. Cepstrum은 이상적으로 기어박스에서 발생되는 것과 같은 다수의 Harmonic 급수들을 포함하고 있는 복잡한 신호들의 분석에 적합하다. Cepstrum은 주파수 영역으로 표시되는데 수직축에는 진폭, 수평축에는 Quefrency라고 불리는 Pseudo Frequency를 나타낸다. 주기적인 함수들을 서로 분리하고 또 강조함으로 해서 신호들 사이의 관계를 알 수 있게 하는 능력은 Cepstrum 분석의 가장 중요한 장점이다. Cepstrum 분석은 흔히 다른 방법을 이용해서는 측대파의 진폭과 간격을 분리해 내기 어려운 경우의 기어상태의 분석에 매우 효과적임이 밝혀졌다.
