3.1 剛性과 變位 (Stiffness and Displacement)
3.2 質量(慣性)과 加速度 [Mass (Inertia) and Acceleration]
3.3 減衰와 速度 (Damping and Velocity)
3.4 全體 시스템의 振動 應答 (Total System Response to Vibration)
3.5 共振時 振動變位와 位相 變化 (Vibration Displacement and Phase Change at Resonance)
Simplified System Dynamics
극히 드물게 예외는 있지만 기계에서 잘못되가고 있는 거의 모든 것은 기계에 의해 발생된 동적인 힘을 증가시키거나 동적인 힘을 제어하는 강성, 질량 또는 감쇠와 같은 정적인 힘을 감소시키는 것이다. 어느 경우든 그 결과는 진동이다. 진동을 일으키는 것은 바로 힘이다. 이러한 힘은 다음 사항에 의해 발생될 수 있다.
① 불평형, Misalignment, 공기 및 수력학적 힘, 기어 이빨의 충격 등과 같은 정상 상태의 가진력.
② Fan, 통풍기 또는 펌프와 같은 유체 취급 설비에서의 난류와 같은 비정상 상태(불규칙적인) 가진력, 가스터빈의 연소난류는 다른 예이다.
③ Rubbing 또는 베어링이나 커플링의 불충분한 윤활에 의해 생긴 마찰.
④ 지나가는 차량, Bumping, 압축기 서징, 기계 기동시 등에 의해 생긴 과도적인 가진력.
각 경우에서 생긴 진동량은 물론 발생한 힘의 크기에 따라 다르지만 관련한 시스템의 강성, 질량 및 감쇠특성에 의해서도 달라진다. 진동력에 대한 Spring-Mass계의 응답에 대한 기본적인 이해가 진동측정, 분석 및 발란싱시 발생한 많은 공통적인 문제들을 이해하고, 확인하고 해결하는데 큰 도움이 될 수 있다. 또한 기계, Piping 또는 구조물의 진동은 가진력을 줄이거나 정적인 힘인 강성, 질량(무게) 또는 감쇠중 하나 이상을 증가시키므로써 감소시킬 수 있다. 예외는 있지만 가진력을 감소시키면 진동치도 감소될 것이다. 그러나 강성, 질량 또는 감쇠를 증가시키면 실제로 진동진폭이 증가할 수도 있다. 따라서 경비와 시간이 소요되는 구조물 개조전에 먼저 진동에 대한 총체적인 정적 저항력 또는 임피던스를 구하기 위하여 어떻게 이들 힘을 조합할 것인가를 아는 것이 중요하다.
2 질량/관성과 가속도
Mass/Inertia and Acceleration
Newton의 제2법칙에 의하면 정지상태의 물체는 정지 상태를 유지하기 위해, 또 운동상태의 물체는 운동상태를 유지하기 위한 성향인 관성을 가지고 있다. 기술적으로는 물체의 질량 즉 관성은 물체에 작용하는 힘을 그 힘으로부터 생기는 가속도(속도의 변화율)로 나눈 비이다. 따라서 질량 즉 관성의 단위는 다음과 같이 쓸 수 있다.
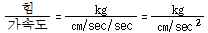
진동주파수와는 전혀 관계없고 변위에 비례하는 함수인 강성과는 달리 질량 즉 관성은 가속도에 역비례하여 변화한다. 그 결과 진동체에서 그 질량 즉 관성은 진동주파수의 제곱에 비례하여 증가한다. 좋은 예가 불평형에 의해 생긴 힘이다. 다음 식으로부터 불평형력은 회전속도의 제곱에 비례하여 증가하는 것을 볼 수 있다.
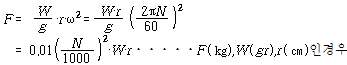
여기서 F = 불평형력
ω = 원진동수 = 각속도 =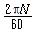 
= 2∏f
r = 불평형 무게까지의 반경
W = 불평형 무게
g = 중력 가속도
N = 회전수(rpm)
3 감쇠와 속도
Damping and Velocity
감쇠는 시스템의 진동 속도를 줄이는 성향이라 할 수 있다. 예를 들면 종과 같은 물체가 타격을 받으면 진동을 일으키는데 그 충격력은 강성 및 질량이 본래부터 가지고 있는 힘을 이겨내지만 궁극적으로 진동은 그림 3-12와 같이 소멸된다. 감쇠가 클 수록 진동은 보다 빨리 소멸하게 된다.
감쇠는 시스템 내의 에너지를 방산하는 역할을 하며, 에너지는 질량×속도의 자승과 같기 때문에 감쇠는 속도에 비례하는 함수이다. 감쇠는 “C”로 나타내며 단위는 ㎏-sec/㎝이다.
전형적인 시스템에서 감쇠의 일반적인 근원으로 점성감쇠(Viscous Damping)와 Coulomb 감쇠가 있다. 점성감쇠는 유체(액체 또는 가스)내에서 물체의 진동 발산이다. 점성감쇠의 예로는 자동차의 Oil 또는 Gas 충격 흡수 장치(Shock Absorber)로써 여기서 Orifice를 통하는 유체의 이동을 제어하므로써 감쇠가 이루어진다. Sleeve Type(수력학적) 베어링의 유막도 점성 감쇠를 가진다.
Coulomb 감쇠는 2개의 건조한 미끄럼 표면의 마찰로부터 진동 에너지의 발산이다. 이 형태의 감쇠를 마찰감쇠 또는 Hysteresis 감쇠라고도 한다. 타격을 받은 종의 경우에 종의 재질 분자간에 발생한 마찰은 궁극적으로 진동이 소멸하는데 필요한 감쇠를 준 것이다. 분자간의 마찰을 통해서 발생한 감쇠의 정도는 분자 구조의 재질과 복잡성에 달려 있다. 예를 들면 주철은 강보다는 보다 효과적인 감쇠를 가지고 있다. 이런 이유로 진동 제어가 극히 필요한 공작 기계의 틀 제작에 있어 강보다는 주철이 일반적으로 선정된다. 초기에 자동차에 사용한 진동흡수 장치는 Coulomb 감쇠를 사용하였는데 조정할 수 있는 볼트 또는 스프링을 장착한 2개의 Absorber Pad로 구성되어 있다. 자동차의 Frame에 대하여 현수장치의 진동이나 이동이 있으면 Pad가 Rubbing하여 감쇠에 필요한 마찰을 일으킨다.
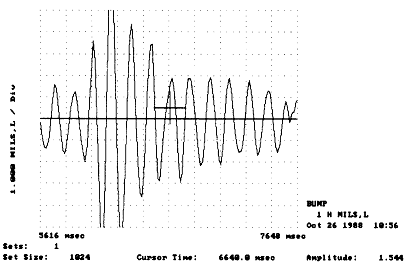
그림 3-12 충격에 의해 가진된 진동이 감쇠로 인해 소멸한다.
감쇠는 진동 속도에 비례하는 에너지의 발산이기 때문에 감쇠는 진동주파수에 직접 비례하는 진동 시스템에서 증가한다.
4 전체 시스템의 진동 응답
Total System Response to Vibration
설명한 바와 같이 이것은 시스템이 주어진 가진에 어떻게 응답할 것인가를 결정하는 강성, 질량(관성) 및 감쇠의 구속력의 조합된 결과이다. 수학적으로는 그 관계를 다음과 같이 쓸 수 있다.
mx” + Cx’ + Kx =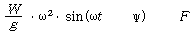 
여기서 x” = 진동 가속도 = -xω2sinωt
x’ = 진동 속도 = xωcos wt
x = 진동 변위
F = 불평형에 의한 가진력
ψ = 가진력과 실제 진동간의 위상각
위식을 간단히 하면 다음과 같이 쓸 수 있다.
가진력 = 강성력 + 관성력 + 감쇠력
다시 말하면 가진력은 강성, 질량(관성) 및 감쇠의 구속력과 항상 평형을 이룬다. 물론 가진력에 의한 진동진폭은 강성, 질량 및 감쇠량의 조합한 효과에 따라 다르다. 그리고 이 3가지 구속력들중 어느 하나의 증가는 진동진폭의 감소를 가져올 것이 분명하다. 그러나 실제로는 이 구속력들이 함께 작용하지 않는다. 이를 설명하기 위해서는 질량(관성)력은 가속도에 비례하고 반면에 강성은 변위에 비례함을 알아야 한다. 앞의 식과 그림 3-13의 진동 파형으로부터 변위 정점 (+)과 가속도 정점 (+)은 실제로 180° 위상차가 있음을 알 수 있다. 그 결과 강성과 질량(관성)의 정적인 힘은 실제로 180° 위상차가 있어 서로 상쇄하려고 한다. 이것으로 보면 감쇠는 속도비례 함수이고 속도는 Cosine 함수이므로 감쇠력은 강성 및 관성 모두에 실제로 90° 위상차가 있다.
종합해 보면 강성, 질량(관성) 및 감쇠의 구속력들은 그림 3-14에 나타낸 바와 같이 벡터량으로 간주되어야 한다. 주어진 가진력으로부터의 진동진폭을 제어할 수 있는 전체 정적인 힘은 산술적인 합이 아니고 강성, 질량 및 감쇠의 벡터합이다.
그림 3-14의 예를 보면 강성력은 3가지 힘중 가장 큰 것이 분명하다. 다시 말하면 이 시스템에서 진동은 시스템의 강성에 의해서 주로 제어되고 있다. 이런 사실을 모르고 진동을 줄이려고 질량을 증가시킬 것을 결정하였다면 그 결과는 진동의 증가를 가져왔을 것이다.
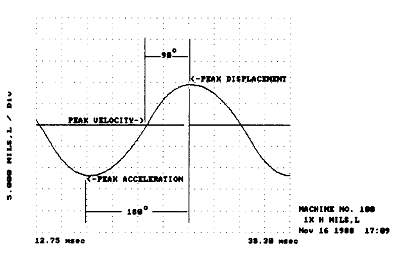
그림 3-13 변위(강성)와 가속도(질량)의 정점은 180° 위상차가 있고 속도(감쇠)
정점은 변위와 가속도와 90° 위상차가 있다.
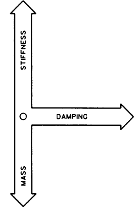
그림 3-14 강성, 질량 및 감쇠는 벡터량이며 탁월한 제어력은 강성이다
또 하나의 중요한 사실은 유효 진동수(ω)는 여러 구속력들의 크기를 가지고 있다는 것이다. 강성은 오직 변위(x)에만 비례하며 따라서 강성력은 가진력의 진동수에 의해 크게 영향을 받지 않는다는 것을 알 수 있다. 다시 말하면 강성력은 진동주파수와 관계없이 일정하다. 한편 관성력은 진동주파수의 제곱에 비례하는 진동 가속도에 비례한다. 다시 말하면 불평형력과 같은 관성력은 진동주파수의 제곱에 따라 증가한다. 그림 3-15는 진동주파수와 강성의 크기와 관성력간의 관계를 보여준다.
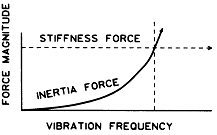
그림 3-15 관성력은 진동주파수의 제곱에 비례하여 증가하고, 반면에
강성은 본래 주파수와는 무관하다.
그림 3-15에서 관성력이 가진력 주파수의 제곱에 비례하여 증가할 때 관성력과 강성력이 크기가 같은 특정 주파수가 있음을 알 수 있다. 그리고 강성과 관성의 구속력이 180° 위상차가 있기 때문에 그들은 실제로 서로 상쇄된다. 결국 강성력과 관성력이 같아져 서로 상쇄되는 주파수에서 그 시스템은 본질적으로 강성과 관성의 구속력을 잃게 된다. 그 결과 주어진 가진력에 대해서 그 시스템은 억제하도록 하는 감쇠력만을 가지는 이 특정 주파수에서 상당히 높은 진동진폭을 나타낼 것이다. 그림 3-16은 진동 주파수의 함수로써 진동진폭으로 환산하여 시스템의 응답을 보여주고 있다.
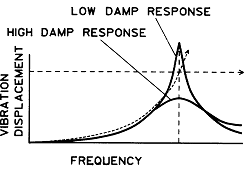
그림 3-16 가장 높은 진동진폭은 강성과 관성이 같아지는 주파수에서 발생한다.
강성 및 관성력이 크기가 같고 가장 높은 진동진폭이 발생하는 진동주파수를 공진 주파수라고 한다. 고유 및 임계 주파수란 용어는 공진과 동의어이지만 임계란 용어는 통상적으로 회전체의 고유 주파수와 같을 때 사용된다.
그림 3-16에서 감쇠가 낮은 시스템은 공진시 커다란 진동 진폭을 나타냄을 볼 수 있다. 높은 감쇠를 가지는 시스템은 공진 주파수에서 낮은 진폭을 가지지만 공진점 이상의 주파수에서는 보다 높은 진폭을 가지게 된다.
5 공진시 진동변위와 위상 변화
Vibration Displacement and Phase Change at Resonance
공진은 가진주파수와 고유진동수가 일치할 때 발생한다. 이는 로터의 고유진동수 이지만 때로는 지지구조물, 기초 또는 심지어 벨트의 주파수일 수 있다. 가진주파수는 불평형, Misalignment, 기계 이완, 베어링 결함, 기어 결함, 벨트 마멸과 같은 것으로부터 생기는 주파수를 포함한다.
그림 3-17은 공진을 설명하는데 좋은 그림으로 수직축에는 확대계수(Q) 또 수평축에는 주파수비(f/fn)를 나타내고 있다. 확대계수는 기계가 공진점을 통과할 때 진동이 얼마만큼 증폭되는가를 나타내는 진폭비이다. 그림 3-17에서와 같이 증폭계수는 부하에 의한 정적처짐(Xst)에 대한 가진 주파수에서 동적처짐(Xo)의 비이다. 다시 말하면 정지시 축의 처짐대 회전시 축의 처짐의 비이다. 주파수비는 고유진동수(fn)에 대한 가진 주파수의 비이다. 그림 3-17의 위 그림은 주파수비가 1.0에 접근할 때(즉 가진 주파수가 고유진동수에 접근할 때)오직 시스템의 감쇠량에 따라서 진동진폭이 아주 높아질 수 있음을 보여준다. 실제로 그림에 나타낸 식에서 공진시 무한대의 진동진폭을 제한하는 것은 오직 시스템 감쇠(감쇠 또는 감쇠계수 ζ라고도 함)뿐임을 보여준다. 강, 알루미늄, 주철 등으로 만들어진 일반적인 기계 구조물에서 감쇠계수는 통상 0.05이하이며, 이 감쇠계수에서는 공진 진폭이 10배가 될것이며 이보다 낮은 감쇠에서는 50배의 진폭이 발생할 수 있다. 따라서 이와같은 진동이 쉽게 발생할 수 있으며 심지어는 가공할 만한 기계손상을 초래할 수 있다.
그림 3-17에 여러 가지 감쇠계수에 대하여 위상지연 대 주파수비를 작도한 것에 유의할 것임. 기계가 공진점을 통과할 때 정확히 고유진동수에서 90°의 위상변화가 생기며 고유진동수 부근에서는 위상이 계속하여 급속히 변화함을 볼 수 있다. 궁극적으로 공진영역을 완전히 통과하면 위상은 거의 180° 변화하게 된다. 전체적인 위상변화와 고유진동수로부터 주어진 거리에 대하여 위상이 변화하는 율은 감쇠량에 의해 제어된다. 감쇠량이 적을수록 위상변화율은 더 커진다.
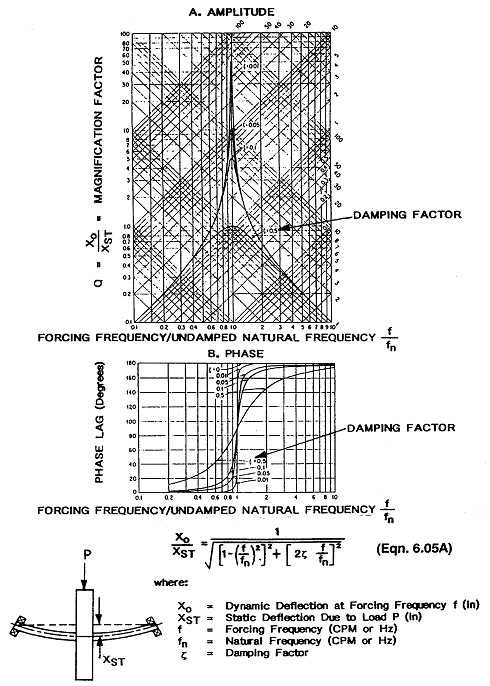
그림 3-17 공진시 공진 진폭곡선과 위상변화
그림 3-18은 Bode Plot과 같으며 3개의 영역(A, B 및 C)에서 로터가 어떻게 응답하는가를 보여주며 또한 각 영역에서 로터의 Heavy Spot(실질적인 불평형 위치)와 최대진동을 나타내는 High Spot(로터의 최대 처짐 위치)의 관계를 보여준다. 일반적으로 임계속도의 70%이하에서 운전하는 로터를 강성 로터라고 하며, 70%이상에서 운전하는 로터는 불평형력 때문에 실제로 휘거나 유연하여 탄성 로터라고 한다. 영역 A는 강성이 동적인 구속력(저항)을 제어하는 곳으로 Heavy Spot과 High Spot간에는 위상차가 거의 없다. 즉 영역 A에서 로터의 진동변위를 다이얼 게이지로 측정할 수 있다면 가장 큰 변위는 거의 Heavy Spot에서 취해질 것이다. 또한 영역 A에서 불평형 진동응답은 회전속도의 자승에 따라 증가할 것이며(속도가 3배 증가하면 약 9배의 진동 변위가 될 것이다), 감쇠량은 진동에 거의 영향을 미치지 못한다.
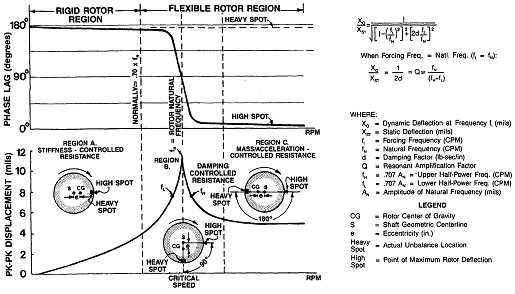
그림 3-18 공진점 및 그 전후에서 회전속도에 따른 진동변 위와 위상각 지연의 변화
그림 3-18에서 로터가 승속하여 영역 B에 들어가면 감쇠로 인하여 High Spot는 어떤 각도만큼 Heavy Spot에 대해 지연되기 시작한다. 이 각도지연(위상지연)은 Heavy Spot가 축 변위를 일으키는데 걸리는 시간의 지연에 의한 것이다. 실제로 로터가 1차 임계속도에 접근하면 Heavy Spot가 90°만큼 회전할 때까지는 최대 진동변위(High Spot)는 발생하지 않는다. 이 90° 위상지연이 공진점에서 발생할 때 무한한 진동응답을 제한하는 유일한 변수는 감쇠량이다.
로터가 계속 승속하여 영역 C에 들어선후 위상지연은 계속 변화하고 마지막으로는 로터가 임계속도 영역을 완전히 벗어나면 위상지연은 180°에 이른다. 이것이 의미하는 바는 로터의 최대처짐점인 High Spot가 실제로 Heavy Spot보다 완전히 180° 지연된다는 것이다. 영역 C에서 동적인 구속력은 강성이나 감쇠로부터 어떠한 구속력(저항)이 없는 거의 순수한 질량에 의해 제어된다. 또한 흥미로운 사실은 1차 임계속도를 훨씬 지나고 2차 임계속도 훨씬 전인 영역 C에서는 원심력(Fc)은 계속하여 속도 자승에 따라 증가할지라도 변위는 거의 일정하다는 것이다. 이러한 이유는 영역 C에서 진동에 대한 구속력은 질량에 가속도를 곱한 것(mω2)에 조정된다. 따라서 원심력이 속도의 제곱에 따라 증가할지라도 운동에 대한 동적인 구속력도 마찬가지로 원심력에 반작용하는 속도의 제곱에 따라 증가하므로 변위는 거의 일정하게 된다.