6.1 一面 발란싱의 利用方法 (The Method of Using Single Plane Balancing)
6.2 벡터 計算法 (Vector Calculation Method)
6.3 彈性 로터의 발란싱 特性 (Balancing Characteristics of Flexible Rotor)
6.4 Static-Couple 成分 分解에 의한 回轉體 발란싱 (Rotor Balancing by Static-Couple Derivation)
6.5 最初 Trial Weight 計算 (Initial Trial Weight Calculation)
6.6 Overhung Rotor의 발란싱 (Overhung Rotor Balancing)
6.7 折衷 발란싱 (Compromise Balancing)
6.8 多面 발란싱 (Multi-Plane Balancing)
1 1면 발란싱의 이용방법
The Method of Using Single Plane Balancing
2면 발란싱할때는 Cross Effect를 고려해야 한다. 이를 발란싱하는 방법은 여러 가지가 있다. 그중 널리 쓰이는 것은 진동이 일어나는 가장 가까운 베어링을 선정하여 각 교정면을 1면 발란싱 문제로 취급하여 동시에 각 교정면을 각기 발란싱하는 것이다. 발란싱 절차는 다음과 같다.
① 양쪽 베어링에서 진동의 진폭 및 위상을 측정기록하고 큰 진동을 갖는 베어링을 선정한다.
② 이미 언급한 벡터도를 이용한 1면 발란싱 방법을 이용하여 가장 높은 진동을 갖는 (제1) 교정면을 발란싱한다.
③ 제1 교정면이 성공적으로 발란스되면 제2 교정면을 발란스하기 위하여 새로운 진폭 및 위상을 측정 기록한다. 이 진폭 및 위상치는 제2의 교정면을 발란싱하는데 있어서의 초기 진동값이다. 제1 교정면을 발란싱한 결과 제2 교정면은 새로운 값을 갖게 된다. 왜냐하면 Cross Effect를 일으키는 제1 교정면의 발란싱 작업이 있었기 때문이다.
④ 새로운 데이터를 이용할 때는 표준 1면 발란싱 벡터기법을 이용하여 제2의 수정면을 발란싱한다.
⑤ 제2 교정면을 발란싱한 후 제1 교정면이 변화한 것을 곧 알게 된다. 제2 교정면의 불평형으로 인한 Cross Effect가 제거되었기 때문이다.
⑥ 만일 Cross Effect가 특히 크면 양쪽 교정면에서의 값이 만족스런 값으로 발란스될때까지 제1 교정면을 발란싱하고 다음 제2 교정면을 발란싱하는 것을 여러번 되풀이 해야된다.
2 벡터 계산법
Vector Calculation Method
만일 Cross Effect가 없다면 2면 발란싱은 3회의 발란싱만으로 끝난다. 불행히도 Cross Effect는 어느 정도는 항상 존재한다. 그러므로 1면 벡터 발란싱기법을 이용하여 좋은 발란스 상태를 얻기 위해서는 여러번 발란싱을 하게 된다. 그러나 어떤 기계는 한번 기동정지하는데 30분으로부터 하루 온종일까지 소요된다. 이러한 기계에 대해서는 발란싱 회수를 최소로 할 수 있는 것이 가장 도움이 된다. 기계를 기동 및 정지하는데 상당한 시간이 소요될때나 심한 Cross Effect가 생길때는 2면 발란싱용 벡터기법을 이용함으로써 이 발란싱문제가 아주 간단하게 될 수 있다. 간단히 말해서 2면 발란싱의 경우 오직 3회의 기동정지 운전만으로 발란싱을 끝낼 수 있다.
한 로터의 양 교정면(N-면, F-면)에서의 초기 불평형의 벡터값(N, F)를 측정 기록한다. 다음에 N-면에 Trial Weight(WNT)를 달고 N, F면에서 진동(N2, F2)을 측정 기록한다. 마지막으로 N면에 달았던 Trial Weight(WNT)를 취외하고 F면에 Trial Weight(WFT)를 달고 또 N, F면에서 진동(N3, F3)을 측정 기록한다. 이상의 기록을 이용하여 N면과 F면에 달아야 할 Balance Weight(WNB, WFB)의 양과 위치를 구하는 벡터 계산식은 다음과 같다. 여기의 N, F 등 모든 양들은 벡터량이다.
| 발란싱 회수 | N-면 | F-면 | Trial Weight | 비교 |
| 0 | N | F | ||
| 1 | N2 | F2 | WNT | N-면에서 (0)Shot 기준 |
| 2 | N3 | F3 | WFT | F-면에서 (0)Shot 기준 |
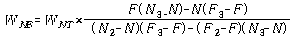
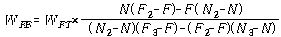
3 연성 로터의 발란싱 특성
Balancing Characteristics of Flexible Rotor
강성 로터를 발란싱하는데는 앞서 기술한 2면 발란싱 절차를 이용하여 2면에서 2개의 Weight를 사용하면 충분하다. 그러나 로터가 불평형력의 영향으로 휜다면 이것은 강성 로터로는 간주할 수 없으며 여러개의 교정면에서 발란스 교정이 필요하게 된다. 또한 1차 임계속도 부근에서 운전하는 로터는 휜상태로 나타나며 2면 이상에서의 발란싱이 필요하게 된다.
다면 발란싱은 직경에 비해 길이가 긴 축이나 또는 불평형에 의한 원심력이 로터를 휘게 하는 경우에 필요하다 (그림 3-31 참조).
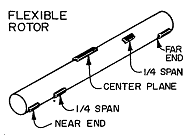
그림 3-31 5면 발란싱 교정을 보여주는 탄성 로터
탄성 로터는 정격속도와 정격온도에서 운전할 때 정적상태로부터 휘거나 비틀린다. 이러한 휨 또는 비틀림은 로터의 질량 분포상태를 변화시켜 불평형 상태가 된다. 따라서 탄성 로터는 저속이나 정상적인 운전조건과 다른 조건하에서 발란스가 되었더라도 정상운전중에는 또 다른 불평형 상태가 나타나게 된다.
정확한 발란스를 위해서는 탄성 로터는 운전상태의 속도, 온도 및 부하에따라 Trim Balancing이 필요하다.
로터가 강성이 아니고 축의 임계속도 부근이나 그 이상에서 운전할때 축 길이에 따라 발란싱 Weight의 위치는 대단히 중요하다. 만일 로터가 전운전 속도에 걸쳐 만족 스럽게 운전해야 한다면 2면 이상의 발란싱이 필요하다.
일반적으로 탄성 로터의 2면 발란싱은 발린싱을 시행한 속도에서만의 발란싱이 된다. 2면 이상에서 로터를 발란싱하기 위해서는 운전속도로 올리기까지 몇 개의 속도에서 로터를 운전할 수 있어야 하고 휨이나 비틀림을 검출하고 교정하기 위한 로터의 휨 또는 비틀림을 구하는 방법이 필요하다.
베어링은 강성이고 여러 속도에서 축의 처짐과 비틀림이 관계되었다면 그 결과를 초래할 수 있는 상황을 그림 3-32부터 3-35까지에서 볼 수 있다.
불평형중 가장 단순한 경우는 그림 3-32와 같이 가늘고 긴 축중심에 설치된 얇은 Wheel이다. 축은 무게가 없고 Wheel의 무게중심은 축의 중심선으로부터 “E”만큼 떨어져 있다고 가정하자. 그러면 불평형량은 Wheel의 무게 “W”와 그 편심 “E”의 곱과 같을 것이다. 만일 Wheel과 축이 수평으로 놓였더라면 불평형의 무게 영향으로 회전하다가 아래쪽에 불평형이 위치한 상태로 정지하였을 것이다. 이것이 Static Unbalance의 간단한 예이다.
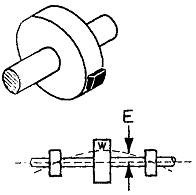
그림 3-32 단순처짐
축이 회전하면 불평형에 의한 원심력으로 축은 휘어져 그림에서 점선으로 나타낸 바와 같이 하나의 Loop 모양을 가진다. 불평형력이 클수록 휨량이 더 커진다. 축과 함께 Wheel이 회전하기 때문에 이것은 진동으로 나타난다. Wheel을 발란싱 하기 위하여 Balancing Weight “Wt”를 축 중심으로부터 반경 “R”인 거리에 불평형 위치와 180°인 곳에 달았다. 따라서 Balancing Weight는 WE = WtR로 구할 수 있다.
이번에는 그림 3-33에서와 같이 발란스가 안된 2개의 Wheel을 가지는 로터에 대해 생각해 보자. 양쪽 Wheel의 편심이 같고 같은 각 위치에 불평형이 있다면 이 로터는 정적으로 불평형 되었고 점선으로 나타난 하나의 Loop 모양으로 운전하게 될 것이다. 이러한 경우는 각 Wheel에 동일한 무게의 Weight를 동일한 반경과 동일한 각도 위에 달게되는 Static Pair 형태로 발란싱하면 교정될 수 있다.
각 Wheel에서의 편심은 같고 180° 떨어져 있다면(그림 3-33B)이 로터는 정적으로는 발란스되어 있지만 동적으로는 그렇지 못하다. 회전하면 점선으로 나타난 2개의 Loop 형태로 휘게 될 것이다. 이러한 불평형의 형태는 동일한 반경과 180° 떨어져서 각 Wheel에 동일한 무게의 Weight를 달면 교정된다. 그림 3-33B와 같은 터빈 발전기에서 탄성 로터의 순수한 Couple Unbalance는 2개의 Loop 모양을 한 로터 휨을 발생시킨다. 불평형 위치는 180° 떨어져 있다. 로터 양끝에서의 Weight와 편심은 같다.
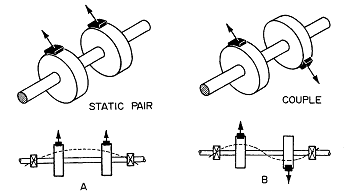
그림 3-33 2개의 Wheel에서 단순처짐
축의 길이가 길고 고속인 탄성 로터에서는 불평형력에 의해 그림 3-34 및 그림 3-35와 같이 3개 또는 4개의 Loop 모양으로 운전될 수 있다.
일반적으로 Static 및 Couple Unbalance는 로터의 양쪽끝 부근의 2개 교정면에서 발란싱 Weight를 달면 교정이 된다. 그러나 3-Loop 형태의 불평형은 각 Wheel에서의 불평형을 교정하기 위해서는 그림 3-34와 같이 3면에서의 발란싱이 필요하다. 마찬가지로 4-Loop 형태의 불평형은 로터가 4-Loop 형태의 휨이 발생할 수 있을만큼 고속으로 회전한다면 그때만 교정이 필요하다.
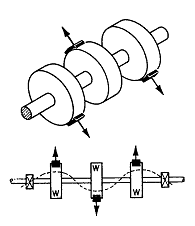
그림 3-34 3개 Wheel 에서의 불평형에 의한 형태
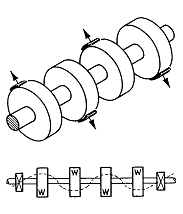
그림 3-35 4개 Wheel 에서의 불평형에 의한 형태
많은 대형 로터는 저속에서 Balancing Machine상에서 발란싱 한다. 2개의 선정한 교정면에서의 불평형량과 각도 위치에 관한 자료를 Balancing Machine의 계측기로부터 읽는다. 로터는 저속에서는 상대적으로 강성이기 때문에 불평형은 벡터적으로만 계산하여 발란싱한다.
4 성분 분해 발란싱 기법
Rotor Balancing by Static-Couple Derivation
6.4.1 Static-Couple 成分 分解節次 (The Procedure of Static-Couple Derivation)
6.4.2 Static-Couple 成分 分解에 의한 발란싱 方法 1 (Balancing Method 1 by Static-Couple Derivation)
6.4.3 Static-Couple 成分 分解에 의한 발란싱 방법 2 (Balancing Method 2 by Static-Couple Derivation)
4-1 정척-커플 성분 분해절차
Rotor Balancing by Static-Couple Derivation
6.4.1 Static-Couple 成分 分解節次 (The Procedure of Static-Couple Derivation)
Static-Couple 방법은 대형 터보 로터를 발란싱하는데 자주 사용되는 다면(3면)발란싱 기법이다. 여기서는 Static-Couple 성분의 분해라고 언급한 이 절차는 다음과 같은 전제를 기준한 것이다.
① 어떠한 상태의 불평형도 Static Unbalance나 Couple Unbalance로, 또는 이 둘의 조합으로 생각할 수 있다.
② Static과 Couple Unbalance가 조합된 경우는 각각 Static과 Couple 성분으로 분해하여 교정할 수 있다.
③ 로터의 무게 중심을 포함하는 교정면이나 그 부근에서 기준 교정면에 있는 Static Unbalance 성분을 교정하면 1차 임계속도 뿐만 아니라 1차 강성(구조물) 공진의 원인이 되는 Static Unbalance는 최소화 될 것이다. 또한 로터 양쪽 끝에 있는 기준면에 있는 Couple Unbalance를 교정하면 2차 강성 모드 및 로터의 2차 임계속도 진동도 최소화될 것이다.
④ Static-Couple 성분 분해의 기법은 분명히 절충 접근방식이며 모든 탄성 로터에 대하여 유효함이 증명 되지는 않았지만 경험상 이 기법은 대형 터보 발전기 로터의 저속발란싱에 적용할 때는 만족스런 결과를 가져옴이 밝혀졌다. 그러나 이 적용은 탄성 로터의 다면 발란싱을 결코 제한 하는 것은 아니다. 많은 산업체 발란싱 기술자는 대형 전동기 회전자와 산업용 Fan과 같은 강성 로터에 적용한다.
⑤ 이 절차에 대한 한가지 요지는 2면 발란싱 문제점에 적용했을 때에도 Static과 Couple Unbalance의 성분으로 분해 하므로써 성가신 Cross-Effect와 씨름하지 않고서도 2개의 기준면에서 동시에 발란싱을 수행할 수 있다는 것이다. 많은 사람들은 기동 및 정지중에 공진점을 반드시 통과해야만 하는 고속 기계를 현장 발란싱하는데 이 방법을 선호한다. 위상지연 정보의 도움을 가지고 Static과 Couple Trial Weight를 달면 그 결과는 거의 항상 진동이 감소된다.
4-2 정적-커플 성분 분해에 의한 발란싱 기법Ⅰ
6.4.2 Static-Couple 成分 分解에 의한 발란싱 方法 1 (Balancing Method 1 by Static-Couple Derivation)
Static-Couple 성분 분해에 의한 발란싱 절차를 좌 우측 교정면에서의 초기 진동치가 다음과 같은 전형적인 Dynamic Unbalance 문제를 이용하여 설명할 수 있다.
좌측 교정면에서의 초기 진동치(OL) = 80 ㎛∠230°
우측 교정면에서의 초기 진동치(OR) = 60 ㎛∠330°
① 극좌표를 사용하여 그림 3-36과 같이 벡터 OL과 OR을 그린다.
② 벡터 OL과 OR의 끝을 연결하고 이 교차선의 중간점을 D라 한다.
③ 원점에서 교차선의 중간점까지 선(OD)을 그린다. 이선이 초기 Static Unbalance인 So를 나타내는 벡터이다. 예를 들면 그림 3-36에서 So=46 ㎛∠270°이다. 좌우측 교정면에 작용하는 Couple 성분은 벡터 AD와 벡터 BD이다. 그림 3-36에서 이 Couple Unbalance Vector들을 원점으로 나란하게 이동시켜 점선으로 표시하였다. 여기서 CL=54 ㎛∠197°, CR=54 ㎛∠17°이다.
Static 및 Couple Unbalance 성분 분해로 인한 벡터들을 가지고 Static Unbalance 이건 Couple Unbalance이건 어느 것이든 먼저 교정할 수 있다. 즉 순수한 Static Unbalance 교정은 Couple Unbalance에 영형을 끼치지 않고 그 반대의 경우도 마찬가지이기 때문에 조그만 주의를 기울이고 Balance Sensitivity를 알면 Static 및 Couple 성분 교정을 동시에 수행할 수 있다. 그러나 간단하게 하기 위하여 다음 예는 먼저 Static Unbalance를 교정하고 다음에 Couple Unbalance를 교정한 것을 설명한다.
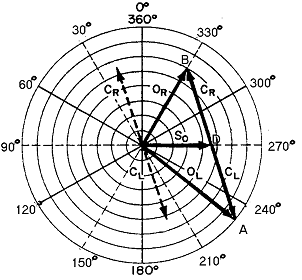
그림 3-36 Static-Couple 성분 분해
④ 그림 3-36에서 초기 Static Unbalance Vector(So)에 대해 Stactic Trial Weight를 달아본다. 이 Static Trial Weight는 그림 3-37A의 예에서 나타낸 바와 같이 로터의 무게중심을 포함하는 기준 교정면에 Single Weight를 달 수 있다. 만일 로터의 중앙 교정면에서 Balance Weight를 달거나 떼낼 수 없으면 그림 3-37B에서와 같이 양쪽끝 교정면에서 나누어 달 수 있다. Static-Couple 성분 분해 기법은 Trial Weight에 의해 발생한 모멘트가 로터의 무게 중심에 대하여 동일한 경우에는 비대칭 로터에도 적용할 수 있다. 이 경우는 기준 교정면의 무게 중심으로부터의 거리의 차이 즉 반경의 차이 때문에 이를 보상하기 위하여 Balance Weight의 조정이 필요하다.
예를 들어 50 gr의 Static Trial Weight를 중앙 기준 교정면에 달았더니 새로운 불평형 진동값이 다음과 같이 되었다고 가정하자.
(O+T)L = 78 ㎛∠184°
(O+T)R = 36 ㎛∠47°
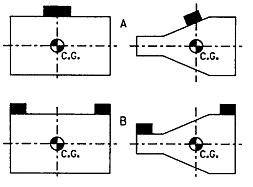
그림 3-37 Static Correction Weight 위치
⑤ 극좌표상에 벡터 OL과 OR을 작도했을때와 같은 눈금으로 벡터(O+T)L과 (O+T)R을 그린다 (그림 3-38 참조).
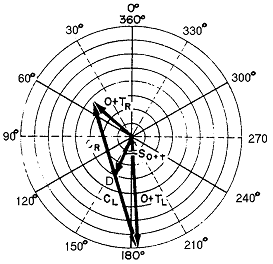
그림 3-38 Trial Weight를 달고 운전한 결과를 나타내는 벡터도
⑥ 벡터 (O+T)L과 (O+T)R의 양끝을 연결하고 이 연결선의 중간점을 D라 한다.
⑦ 원점으로부터 이 연결선의 중간점까지 선(OD)을 긋는다. 이것이 초기 Static Unbalance와 Trial Static Unbalance를 더한 벡터(So+T)이다. 그림 3-38에서 So+T=29 ㎛∠158°이다.
[참고 사항]
벡터 (O+T)L과 (O+T)R을 연결한 선과 그림 3-36에서의 연결선은 길이가 같고 평행(각도가 같음)함에 유의 할 것. 이것은 Static Trial Weight가 무게중심을 포함하는 기준 교정면에 위치하였고 Couple Unbalance는 어떠한 영향을 받지 않았음을 의미한다. Static과 Couple Trial Weight는 서로 간섭하지 않으므로 Static 및 Couple 발란싱을 동시에 시행하여도 문제가 되지 않는다.
⑧ 그림 3-36에서 벡터 So(46 ㎛∠270°)와 그림 3-38에서 So+T=(29 ㎛∠158°)를 이용하여 Static Unbalance를 1면 벡터 해로 구하여 교정할 수 있다 (그림 3-39 참조). 합성벡터 ST=63 ㎛이고 이것으로 교정 Weight를 계산할 수 있다.
CW = TW×O/T = 50 gr×46 ㎛/63 ㎛ = 36.5 gr
벡터 So와 ST 사이의 각도는 25°이므로 벡터 ST가 원점으로 향하기 위해서는 시계 방향으로 25° 이동해야 한다. 따라서 Trial Weight도 시계 방향으로 25°이동하면 된다. 즉 초기 Trial Weight(50 gr)를 떼고 36.5 gr의 Trial Weight를 만들어 원래 설치했던 위치에서 시계 방향으로 25° 옮겨 달면 진동교정이 완료된다.
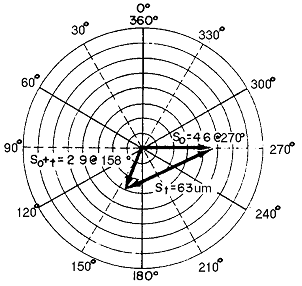
그림 3-39 Static 진동성분을 나타내는 벡터도
⑨ Static Unbalance를 허용치 이내로 감소시키기 위해서는 앞의 5～8단계를 반복하면 된다. 만일 Static Unbalance가 완전히 발란싱 되었다면 그 결과는 진폭은 같고 위상은 180° 서로 다른 Couple Unbalance만 남게된다. 예를 들어 그림 3-36에서 Static Unbalance가 제거되고 나머지 Couple Unbalance의 값은 다음과 같다.
CL = 54 ㎛∠197°, CR = 54 ㎛∠17°
⑩ 나머지 Couple Unbalance는 그림 3-39A에서와 같이 Couple 형태로 Trial Weight를 달면 교정된다. 벡터 계산은 왼쪽이나 오른쪽에서 진동 측정치를 이용하면 가능하다. Trial Weight나 교정 Weight를 달 때 동일한 Weight를 양끝에서 서로 180°되게 달면된다.
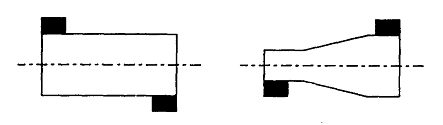
그림 3-39A Couple Unbalance 교정
⑪ Couple 형태의 Trial과 교정 Weight를 달아 표준 벡터법을 이용하여 Couple Unbalance를 발란싱 한다.
터보 발전기나 다른 탄성 로터의 저속 발란싱을 위해 Static-Couple 발란싱 기법을 사용할 때 일반적인 관례는 무게 중심의 기준 교정면에 교정 Weight를 집중시키는 대신에 로터 길이에 따라서 여러 개의 기준 교정면에 Static 교정 Weight를 나누어 다는 것이다. 이 관례는 로터의 Static Unbalance는 중앙에 집중되지 않고 전 로터의 길이에 따라 분산되었다는 가정에 근거를 두고 있다. 따라서 전 로터의 Static Unbalance가 중앙에서 Single Weight로만 교정된다면 임계속도에서 과도한 처짐이 발생하고 정상 운전속도에서 과도한 불평형 진동을 초래할 것이다.
4.3 정적-커플 성분 분해에 의한 발란싱 기법Ⅱ
Balancing Method 2 by Static-Couple Derivation)
Static-Couple 성분 분해에 의한 방법1은 Trial Weight에 의해 생긴 모멘트가 로터의 무게 중심에 대하여 동일한 경우에는 대칭이나 비대칭 어느 로터에도 적용할 수 있다. 그러나 실제 기계에 있어서는 발란스 교정면이 한정되어 있고 Weight를 달아야 할 반경도 정해져 있다. 또한 실제 기계에 있어서는 비록 대칭형인 경우라도 완전한 대칭은 없고 Misalignment와 같은 외적인 진동원인 및 시스템의 감쇠, 강성 등의 차이로 양 베어링에서의 진동특성, Cross-Effect 및 Balance Sensitivity가 다르다.
한편 Static-Couple 성분 분해에 의한 방법 2는 진동 측정시 Pickup, 진동분석기, 설치위치 및 측정방법을 동일하게 하면 계측기의 위상지연 각도, 로터의 위상지연 각도 및 Cross Effect를 모르고서도 Pair Static 및 Couple Trim Balancing을 실시하여 Balance Sensitivity를 구하므로써 교정 Weight를 달면 3회의 기동 정지로 발란싱이 완료된다. 또한 이미 Balance Sensitivity를 알고 있으면 1회의 발란싱으로도 교정이 가능하다. 방법 2는 가장 많이 사용되는 현장 발란싱 방법이다.
예로써 방법1(6.4.2항)과 동일한 초기 진동치를 가진 로터를 발란싱하여 보자.
① Original Vibration Data
그림 3-36의 초기 진동 상태를 그림 3-40과 같이 다시 표현하고 다음과 같이 성분 분해할 수 있다.
좌측 교정면에서의 초기 진동치(OL) = 80 ㎛∠230°
우측 교정면에서의 초기 진동치(OR) = 60 ㎛∠330°
좌측 교정면에서의 Couple Unbalance(CL) = 54 ㎛∠197°
우측 교정면에서의 Couple Unbalance(CR) = 54 ㎛∠17°
좌우측 교정면에서의 Static Unbalance(SO) = 46 ㎛∠270°
앞에서 Static Balancing을 하여도 Couple 성분에 영향을 미치지 않으며 그 반대의 경우도 성립한다고 하였다. 이 로터에서 완벽한 Static Balancing이 이루어진다면 즉 So 값이 0이 된다면 좌우 교정면에서의 OL 및 OR이 CL 및 CR로 변하여(점 A와 B는 점 E와 F로 이동) Couple 성분만 남게된다. 이 상태에서 완벽한 Couple Balancing이 이루어진다면 CL 및 CR은 원점으로 이동되어 진동이 0이 된다.
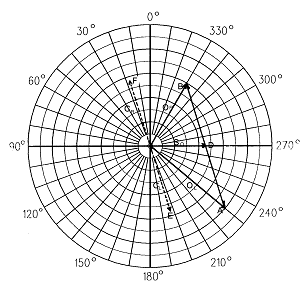
그림 3-40 초기 진동치의 성분 분해
② Static Trial Weight
예를 들어 50 gr의 Static Trial Weight를 Mid Span 또는 양쪽끝의 교정면 90°위치에 달고 운전하였더니 다음과 같이 새로운 진동값을 얻었다고 하자 (그림 3-41 참조).
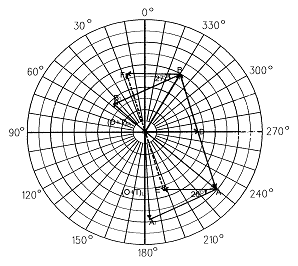
그림 3-41 Trial Weight에 의한 Static Unbalance 교정 벡터도
좌측 교정면에서의 진동치 (O+T)L = 78 ㎛∠184°
우측 교정면에서의 진동치 (O+T)R = 36 ㎛∠47°
③ Static Correction Weight
점A1 및 B1이 점E 및 F로 향하기 위하여서는 좌우 교정면의 Trial Weight를 (26°+27°)/2 = 26.5° 시계 방향으로 이동시킨다. 즉 Trial Weight를 처음에 90°에 달았으므로 90° – 26.5° = 63.5°에 교정 Weight를 달면 된다. 한편 좌우 교정면에서 Trial Weight에 의한 효과 벡터 AA1=64 ㎛, BB1=62 ㎛이므로 이를 평균한 벡터값은 (64+62)㎛/2 = 63 ㎛이다. 이 로터가 원래 가지고 있는 Static Unbalance의 크기 (SO)는 46 ㎛이므로 교정 Weight의 무게는 50 gr × 46 ㎛/63 ㎛ = 36.5 gr이다. 즉 Trial Weight를 떼고 교정 Weight를 좌우 교정면 각각에 36.5 gr을 63.5°에 달면 된다.
이와 같이 Static Balancing 완료후 좌측 교정면에서의 진동치는 그림 3-41에서 벡터 AA1을 A를 기준으로 26.5° 시계 방향으로 이동한 선상의 36.5 gr/50 gr×64 ㎛
46.72 ㎛인 곳이 되고 우측 교정면에서의 진동치는 벡터 BB1을 B를 기준으로 26.5° 시계 방향으로 이동한 선상의 36.5 gr/50 gr×62 ㎛
45.26 ㎛인 곳이 된다. 이 예제에서는 발란싱후 좌우 교정면에서의 예상 진동치가 거의 E1 및 F와 같다. 만일 차이가 나면 새로운 진동치를 직선으로 긋고 그 중앙점이 Couple Balancing의 목표점이 된다.
④ Couple Trial Weight
Static Balancing후 좌우 교정면에서의 진동값이 점 E와 F로 이동되었다고 하면 그림 3-40에서와 같이
좌측 교정면에서의 Couple Unbalance(CL) = 54 ㎛∠197°
우측 교정면에서의 Couple Unbalance(CR) = 54 ㎛∠17°
이 상태에서 좌측 교정면에는 50 gr∠180°, 우측 교정면에는 50 gr∠0°의 Couple Trial Weight를 달고 운전하였더니 그림 3-42와 같았다.
좌측 교정면에서의 진동치 (OE1) = 76 ㎛∠155°
우측 교정면에서의 진동치 (OF1) = 60 ㎛∠330°
좌측 교정면에서의 효과벡터 (EE1) = 46 ㎛∠266°
우측 교정면에서의 효과벡터 (FF1) = 50 ㎛∠107°
∠E1EO=89°, ∠F1FO=70°
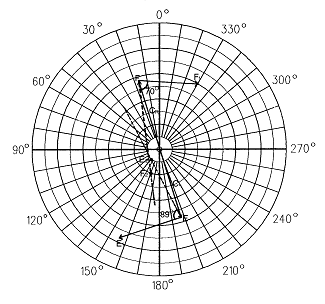
그림 3-42 Trial Weight에 의한 Couple Unbalance 교정 벡터도
⑤ Couple Correction Weight
좌우 교정면에 달아야 할 교정 Weight의 위치는 (78° + 89°)/2 = 79.5°만큼 효과벡터 EE1 및 FF1을 E, F를 기준으로하여 시계 방향으로 이동한 선상에 있다. 좌우측 교정면에 Trial Weight를 180° 및 0°에 위치시켰으므로 이를 떼고 교정 Weight는 180° – 79.5° = 100.5° 및 0° – 79.5° = 280.5°에 달면 된다.
한편 달아야할 교정 Weight의 무게는 효과벡터(EE1 및 FF1)의 평균치 (46 ㎛ + 50 ㎛)/2 = 48 ㎛를 이용하여 E, F점이 원점으로 이동하려면 CL=CR=54 ㎛ 만큼에 해당하는 교정 Weight를 달아야 한다. 즉 좌우측 교정면에는 50 gr
54 ㎛/48 ㎛
56 gr의 교정 Weight를 좌측 교정면에는 100.5°에, 우측교정면에는 280.5°에 각각 달면 된다. 이와 같이 Couple Correction Weight를 달면 실제 진동은 좌측 교정면에서는 벡터 EE1을 E를 기준하여 79.5° 시계 방향으로 이동한 선상에 56 gr
46 ㎛
51.5 ㎛ 거리에 있는 E2점이 되며 진동치는 대략 10 ㎛∠140°이 될 것이다. 한편 우측 교정면에서는 벡터 FF1을 F를 기준하여 79.5° 시계 방향으로 이동한 선상에 56 gr/50 gr
50 ㎛ = 56 ㎛ 거리에 있는 F2점이 되며 진동치는 대략 20 ㎛∠160°가 될 것이다.
5 초기 시동 중량 계산
Initial Trial Weight Calculation
Trial Weight가 너무 작으면 진폭 및 위상변화가 나타나지 않을 것이고, 발란싱하는 자체가 시간과 경비의 낭비일 뿐이다. 반면에 너무 큰 Trial Weight를 달면 특히 위험속도를 통과할 때 기계에 손상을 주게 되므로 시험을 못하게 되는 경우도 있다. 따라서 일반적으로 진폭의 30% 변화 또 30% 위상변화를 생기게 하는 Trial Weight를 계산하여 선정하는 것을 목표로 한다.
(1) Hight Spot Number Chart 이용방법
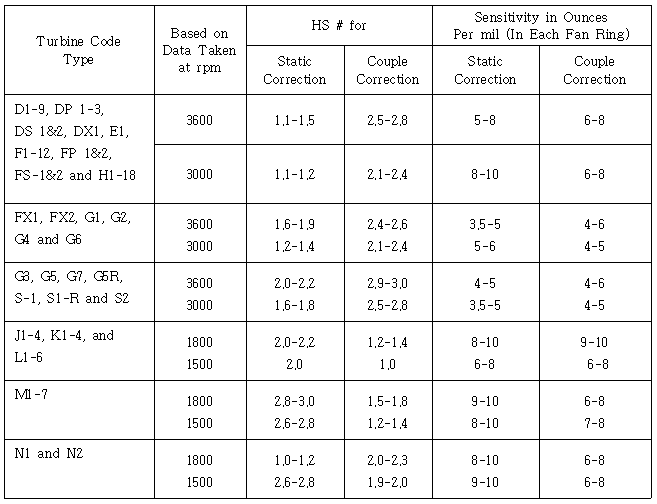
1면 발란싱시 위상각 측정방법을 그대로 2면 발란싱에서도 적용하면 된다. 특히 터빈 Code, Rotor Type, 정격속도, 최종단 동익길이 및 Exhaust Hood Type별로 또한 위험속도와 정격속도에서 불평형 형태(Static Unbalance와 Couple Unbalance)별로 High Spot Number와 Balance Weight Sensitivity가 표시된 High Spot Number Chart를 제작자가 제시하는 경우가 있다. 따라서 이 Chart에 있는 Balance Weight Sensitivity(gr/㎛ 또는 Oz/mil)를 그대로 적용하면 된다 (표 3-2, 3, 4 참조).
(2) Unbalance Force와 로터 중량 이용방법
베어링 부하의 10%와 같은 양의 불평형력이 생기도록 하는 Trial Weight 중량을 선정하는 방법이다.
N rpm으로 회전하는 기계에 Trial Weight
를 반경 (r)에 달았을 때 불평형력 F는
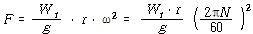
인 경우
인 경우
표 3-2 터빈 High Spot Number & Sensitivity Chart Ⅰ-1
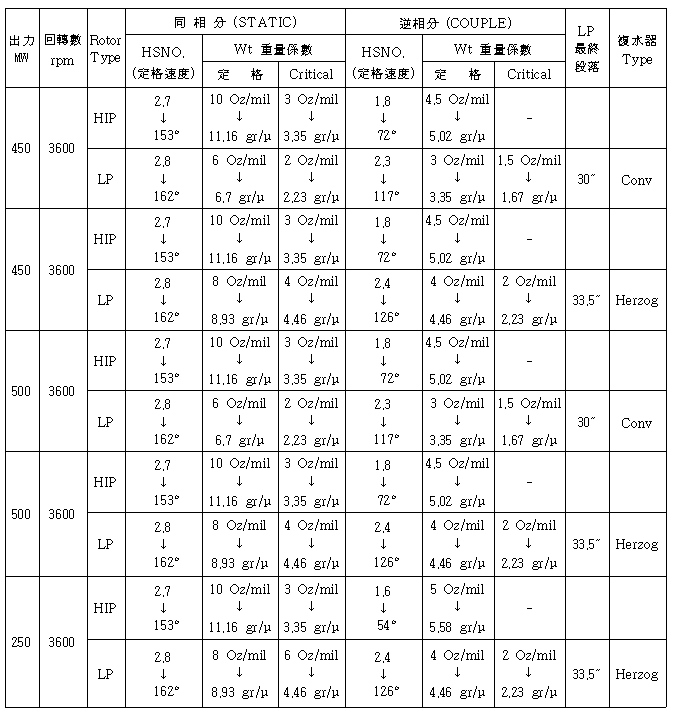
표 3-2 터빈 High Spot Number & Sensitivity Chart Ⅰ-2
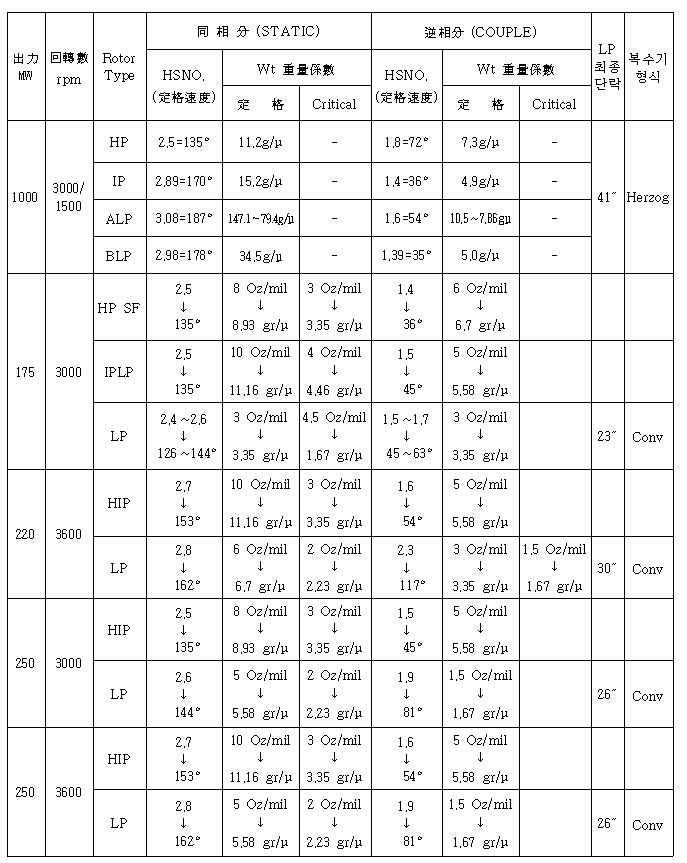
표 3-2 터빈 High Spot Number & Sensitivity Chart Ⅰ-3
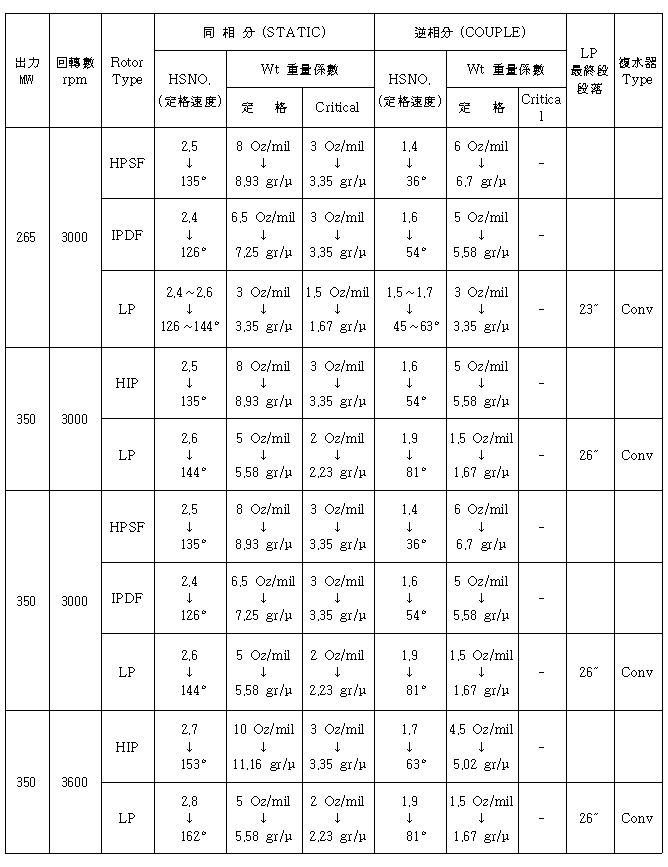
표 3-2 터빈 High Spot Number & Sensitivty Chart Ⅰ-4
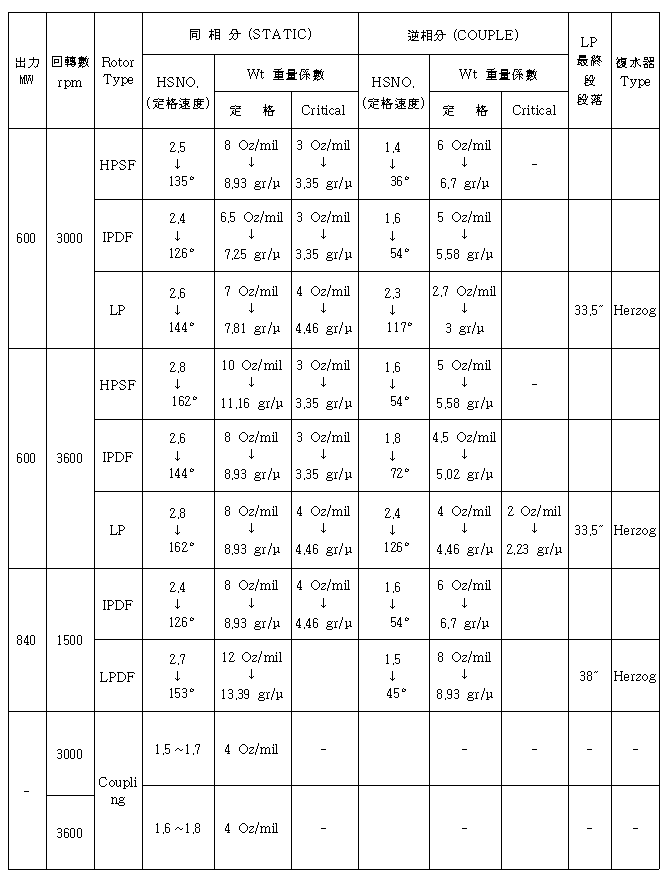
표 3-2 터빈 High Spot Number & Sensitivity Chart Ⅱ-1
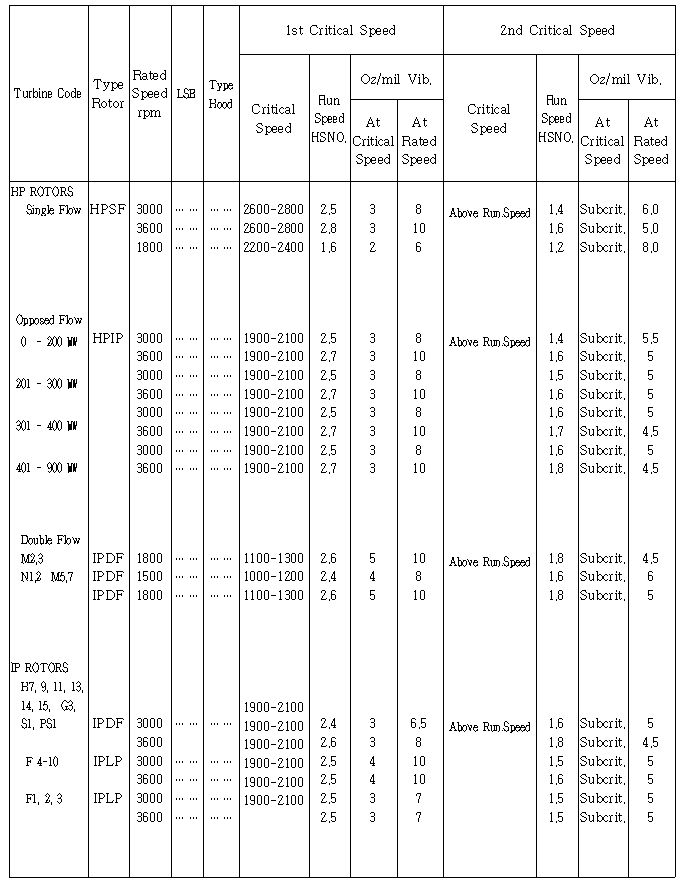
표 3-2 터빈 High Spot Number & Sensitivity Chart Ⅱ-2
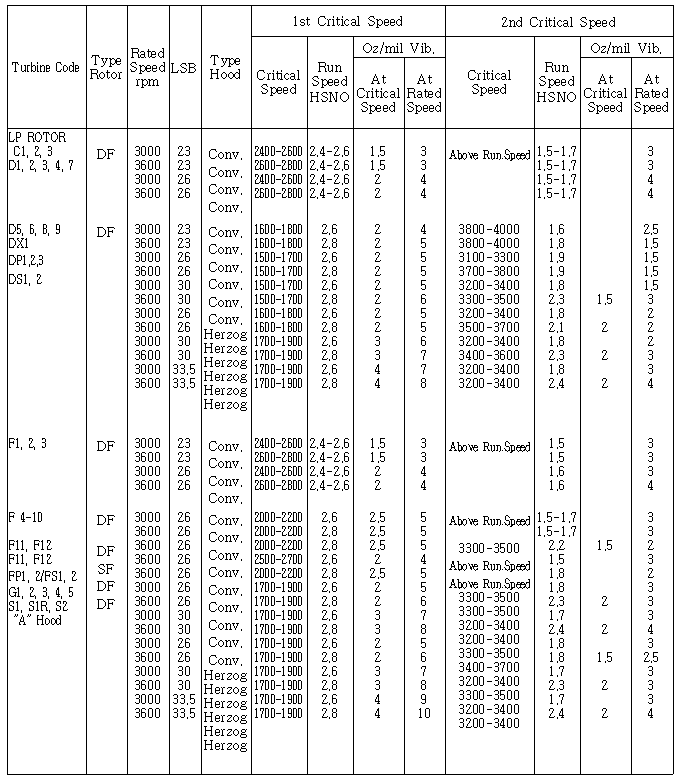
표 3-2 터빈 High Spot Number & Sensitivity Chart Ⅱ-3
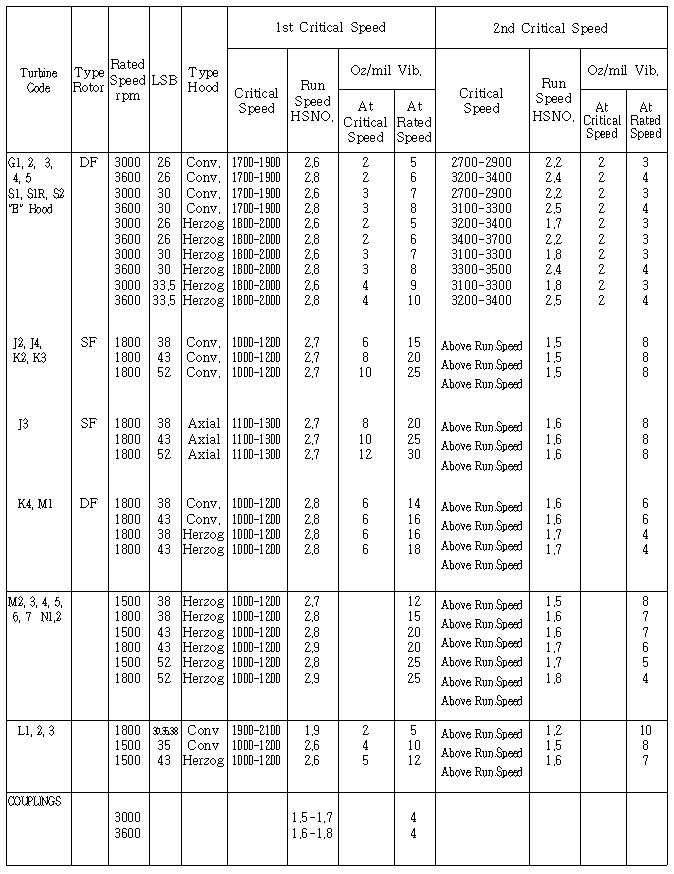
표 3-3 여자기 High Spot Number & Sensitivity Chart
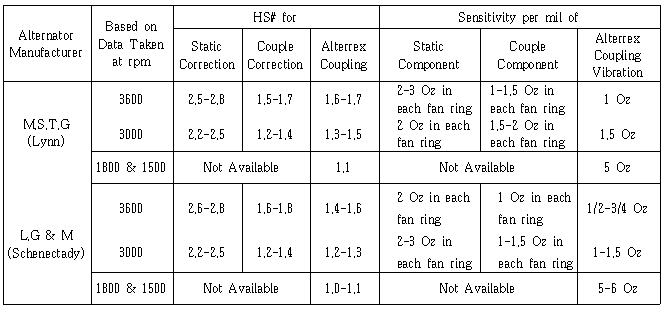
표 3-4 발전기 High Spot Number & Sensitivity Chart
예로써 3600 rpm으로 회전하는 로터의 무게는 20,000 ㎏이고 Balance Weight를 달 수 있는 곳은 로터의 반경 80 ㎝이다. 이 로터를 지지하고 있는 각 베어링에서의 부하는 20,000 ㎏/2 = 10,000 ㎏이고, 각 교정면에 달 최초 Balance Weight는 베어링 부하의 10%인 1000 ㎏에 의한 Force(원심력)에 상당하는 양이다.
다시 말하면 불평형력(F)과 로터 중량(
)과의 관계는
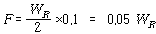
앞의 두 공식을 이용하면 Trial Weight
의 중량은 다음과 같다.
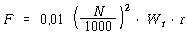
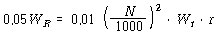
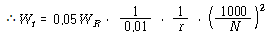
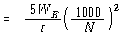
앞에서
= 20,000 ㎏, r = 80 ㎝, N = 3600 rpm이므로
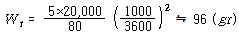
(3) Unbalance Force와 진동진폭 이용방법
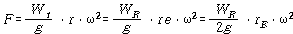
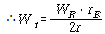
여기서
= Trial Weight (gr)
re = O-P 진폭 (㎛)
= p-p 진폭 (㎛)
= 로터 중량 (㎏)
r = Trial Weight 부착반경 (㎜)
현장에서 실제로 Weight Balancing할 때는 앞의 계산식의 50～70% 정도의 Trial Weight 중량을 선정한다.
(4) 소형 강성 로터의 경우
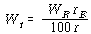
여기서
= Trial Weight (gr)
= p-p 진폭 (㎛)
= 로터 중량 (㎏)
r = Trial Weight 부착반경 (㎜)
6 매달린 축의 발란싱
Overhung Rotor Balancing
그림 3-43에서 보는 바와 같이 Overhung Rotor는 2개의 지지 베어링 바깥쪽에 Fan Wheel을 가진 형태의 기계이다. 이와 같은 모습은 Fan 및 펌프 등과 같은 기계에서 종종 볼 수 있다. 이들 로터는 발란싱해야할 면이 지지 베어링 바깥쪽에 위치하기 때문에 표준의 1면 및 2면 발란싱 방법으로는 교정되지 않는 경우가 종종 있다. 다시 말하면 불평형 교정면이 지지 베어링 밖에 있기 때문에 비록 Static Unbalance만 있다 하더라도 로터 무게중심에서 교정면까지의 거리에 비례하는 Couple Unbalance가 생긴다. 그러므로 Overhung Rotor를 발란싱할 때 분석가들은 Static 및 Couple Unbalance Force 두 가지 모두 고려해야 한다.
Overhung Rotor를 발란싱할 때 다음과 같은 두 가지 절차중의 하나를 선택해야 한다.
(1) 전형적인 1면 Static-Couple Method에 의한 Overhung Rotor의 발란싱
그림 3-43은 Overhung Rotor 발란싱 방법을 설명하는데 도움을 준다. 전형적으로 베어링 A는 Static Unbalance에 아주 민감한 반면, 교정된 Fan Wheel로 부터 멀리 떨어진 베어링 B는 Couple Unbalance에 아주 민감하다. 교정면 ①은 로터의 중심(CG)에 가깝기 때문에 Static 교정은 베어링 A에서의 응답을 측정한 후 교정면 ①에서 행해져야 한다. 반대로 교정면 ②에서 Couple 교정을 할 때에는 B 베어링에서 측정이 이루어져야 한다. 그러나 교정면 ②에 Trial Weight를 달면 베어링 A에서 얻은 Static Balance가 흐트러질 것이다. 따라서, 베어링 A에서의 Static Balance를 유지하기 위하여 Couple 형태로 Trial Weight를 사용하여야 한다.
따라서 1면 발란싱 Software를 이용하여 Data Collector를 사용하거나 로터 길이와 직경의 비(L/D)가 대략 0.5이하인 많은 Overhung Rotor에는 Single-Plane Graphic 기술을 사용한다 (여기서 L은 교정 Weight가 취부된 회전부분의 길이이며, D는 이 회전부분의 직경이다).
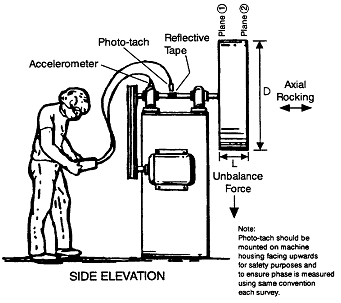
그림 3-43 Overhung Rotor 발란싱용 계측장비 설치
Overhung Rotor에 대한 전형적인 Single-Plane 발란싱 기술을 설명하면 아래와 같다.
① Data Collector와 Spectrum Analyzer Instruments를 설치한다.
2면 절차를 보여주는 그림 3-43에서 언급한 바와 같이 Data Collector, Photo- Tach, 가속도계 등이 설치되어야 한다. 분석자는 Strobe Light를 사용하는 Swept-Filter 분석기를 사용하거나, 위상 측정을 위해 Photo-Tach를 동작시키는 스펙트럼 분석기를 사용한다.
② 초기 측정치를 구한다.
어떤 Trial Weight를 부착하기 전에 1×RPM의 진폭, 주파수, 위상의 초기치를 측정한다. 내 외측 베어링의 수직 및 수평 방향 진동을 측정한다. 반경 방향의 측정치가 제일 큰 교정면을 먼저 발란싱 한다 (불평형 교정후 진폭이 허용치 내에 있는가 확인하기 위하여 다른 반경 방향의 진동치도 측정되어야 한다).
③ 주된 문제가 Static 또는 Couple Unbalance인가를 결정한다.
양 베어링의 수평방향에서 측정된 진폭과 위상치를 살펴보고, 주된 문제가 Static 또는 Couple Unbalance인가를 결정한다. 만약 내 외측 베어링간의 위상차가 수직및 수평 방향에서 거의 140°이상이라면 Couple Unbalance가 우세하다. 반면에 이들 위상차들이 어느 곳에서든지 대략 0°～40°라면 Static Unbalance가 우세하다. 물론 대략 40°에서 140°까지 범위의 위상차는 Static 및 Couple의 조합인 Dynamic Balance 문제이다. 그러나 만약 문제가 주로 Couple Unbalance로 나타나면 아래에 언급된 Couple Unbalance 절차를 사용한다. 그러나 만약 문제가 현저하게 Static 또는 Dynamic Unbalance로 나타나면 Static Balancing 절차를 사용한다. 왜냐하면 지금 우리는 문제가 주로 Static이라고 가정하고 있기 때문이다.
④ 1면 Static Balancing을 한다.
그림 3-43를 참조하여 A베어링 위에서 1면 발란싱 기술을 사용하여 측정 데이터를 얻고, 교정면 ⓛ에 Trial 및 교정 Weight를 취부한다.
⑤ 교정결과 진동 진폭이 요구되는 기준에 일치하는지를 확인한다.
교정면 ⓛ에서 Single-Static Balancing을 한후 내 외측 베어링에서 각 방향(Axial 포함)의 진동측정을 반복하고 진폭이 허용기준에 일치하는지를 확인한다.
⑥ 만약 상당한 Couple Unbalance가 남아 있다면, 베어링 B로 부터 1면 발란싱을 계속한다.
Overhung Rotor는 종종 큰 Cross-Effect를 가지므로써 교정면 ⓛ에서의 1면 발란싱이 종종 B 베어링에서 높은 진동을 일으킨다. 그러므로 분석가는 이번에는 발란싱해야할 부분으로부터 멀리 떨어진 B 베어링으로부터 측정을 하여 또 다른 1면 발란싱을 시행한다. 1면 교정 Weight 해답을 구하여 교정면 ②에 이 Weight를 취부한다. 그리고 나서 교정면 ②에 Weight 위치로부터 약 180° 떨어진 교정면 ①위에 똑같은 크기의 교정 Weight를 취부한다.
⑦ 진폭이 모든 허용 기준치에 일치하는가를 확인한다.
Single-Plane Couple 교정을 한후 분석가는 각 베어링 위에서 수평, 수직, 축 방향 진동을 다시 측정해야 하며, 현재의 모든 진폭이 허용 기준치에 일치하는가를 확인한다.
⑧ 각 베어링의 3 방향에서 허용 기준에 만족하지 않으면 아래에 언급된 2면 발란싱 절차를 행한다.
특히 L/D비가 0.5보다 크거나 발란싱되어야할 기계가 가까운 베어링으로부터 너무 멀리 떨어져 위치한다면 가끔 이 1면 발란싱 방법은 각 베어링에서의 진폭을 세 방향 모두에서 허용 기준치 이내로 성공적으로 줄일 수가 없다. 이러한 경우, 아래에 언급된 2면 발란싱 기술을 사용해야 할 것이다.
(2) 전형적인 2면 Static-Couple Method에 의한 Overhung Rotor 발란싱
Overhung Rotor에서는 큰 Cross Effect가 자주 나타나기 때문에 1면 발란싱 기술을 사용하는 것보다 2면 발란싱 교정기술이 더 성공적이다. 그러나 2면 발란싱 방법에서는 베어링 또는 교정면의 위치 즉 전후좌우를 확실히 하여 혼동을 피하여야 한다.
대부분의 Overhung Rotor는 Static Unbalance에 대단히 예민하므로 이 Static /Couple 성분의 해답이 얻어진 후 Static 교정 Weight를 취부한다. Trim Balancing후 만약 Couple Unbalance가 상당히 남아 있다면 아래 절차에 따라 교정한다.
① 그림 3-43에서와 같이 2면 발란싱 방법을 수행할 수 있도록 계기를 설치한다.
여기서도 Data Collector, Swept-Filter Analyzer 또는 Real-Time Analyzer를 가지고 같은 절차로 시행할 수 있다. 그러나 만약 Swept-Filter 또는 Real Time Analyzer를 사용한다면 분석가는 Static/Couple 해답을 제공할 수 있는 Two Plane Calculator Program을 가져야 한다.
② 양 베어링에서 초기 진동 측정치를 취한다.
여기서도 내 외측 베어링에서 수평, 수직, 축 방향의 1×RPM 진폭, 주파수, 위상이 측정되어야 한다.
③ 2면 발란싱 절차를 마친 후 교정 Weight를 취부하지 말 것.
2면 발란싱 절차를 사용해야 하지만 최종 교정 Weight를 취부하지 않는다. 각 교정면에 대한 Trial Weight 크기와 위치가 계산되었을 때 분석가는 Static/Couple 해답을 구하여 처음에는 Static 교정만 한다. 예를 들면 만약 Static 해답이 교정면 ①에 100 gr이 필요하고, Couple 해답이 교정면 ① 및 ②의 서로 반대면 180°에 200 gr이 필요하다면, Static 교정만 한다.
④ 진폭이 허용기준에 일치하는지를 확인한다.
교정면 ①에 Static 교정을 한 후 각 베어링에서의 세 방향 모두의 진폭이 허용기준치 이내에 있는지 본다. 만약 만족하지 않으면 다시 Trim Balance를 한다. 2면 발란싱 교정이 결정되면 Static 및 Couple 해답을 보고, 한번 더 Static 교정만 한다. 이때 대부분의 문제들이 해결된다. 만약 상당한 크기의 Couple Unbalance가 여전히 남아 있으면, Static 및 Couple 해답을 보고 한번 더 2면 발란싱을 절차를 행한다. 이번에는 Static 교정이 아니라 Couple 교정을 한다.
⑤ 진폭이 허용기준치에 일치하는지를 확인한다.
두번의 Static 교정 시도 및 한번의 Couple 교정 시도후 내 외측 베어링에서 수평, 수직, 축 방향의 진폭이 허용기준치 이내에 있는가를 비교 검토한다.
7 보정 발란싱
Compromise Balancing
6.7.1 熱的 敏感度 (Thermal Sensitivity)
열적 민감도란 부하, 증기조건, 물이나 증기 밀봉상태 조정, 계자전류, Cold Gas 온도와 압력 및 베어링 오일 입구온도 등과 같은 운전조건의 변화에 의한 진동의 많은 변화를 설명하는데 사용되는 용어이다. 만일 운전조건의 변화로 인해 1×RPM 진동성분이 60 ㎛ 이상 변화하면 열적 민감도에 대해 고려해야하며 이 벡터 변화를 열적벡터(Thermal Vector)라 한다.
그러나 새 발전기의 경우 시운전 초기 단계에 무부하와 전부하 사이에 60～80 ㎛의 벡터 변화는 있을 수 있는 경우이므로 열적 민감도와 혼동해서는 않된다. 이 벡터 변화는 통상적으로 로터의 구성품 즉 Field Copper, Retaning Ring 등의 제자리 잡기와 여자 전류가 처음으로 가압되고 증가될 때 Field Forging의 열적 안정 때문에 발생한다.
터빈과 발전기 로터의 열적 민감도의 주요원인은 다음과 같다.
① 축의 열에의한 민감도
② Shaft Bore내의 물이나 기름의 유입
③ 회전체 부품간의 불균일한 열전달
④ Wheel의 이완 및 Bushing의 고착
⑤ Buchet 등 부품의 이완 및 조립불량
⑥ 비대칭형의 Ventilation
⑦ 계자권선의 단락
이들 원인의 대부분은 로터의 원주둘레의 온도 변화를 초래하여 로터를 휘게하고 진동을 초래한다고 일반적으로 믿고 있다. 열적 민감도의 원인은 하나의 운전변수를 동시에 변화시킴으로써 구할 수 있다.
특히 발전기 용량이 500 MVA를 초과하는 발전기 로터는 2차 모드와 3차 모드 사이에서 운전되므로 축 굽힘 및 다른 원인들에 의해 동상의 불평형 민감도(In-Phase Unbalanced Sensitivity)가 증가한다. 그러므로 기존의 기계적 불평형과 더불어 열적 및 전자기적인 불평형에 대한 발란싱이 필요하다.
6.7.2 折衷 발란싱 節次 (Compromise Balancing Procedure)
열적 민감도가 높은 발전기와 같은 경우 전부하에 걸쳐 진동치가 허용치 이내에 들도록하는 Weight Balance를 절충 발란싱이라 한다. 그림 3-44에 예를 들어 절충 발란싱 절차를 설명한다.
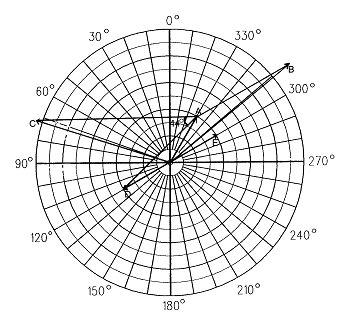
그림 3-44 보정 발란싱의 예
① 정격속도에서의 무부하, 25%, 50%, 75%, 100% 부하시의 진동진폭 및 위상값을 전 베어링, 커플링 및 Collector Ring에서 취한다. 또한 무효전력, 여자전류, 발전기 Cold Gas 온도 및 압력, 계자온도, 베어링 오일의 입출구 온도 등을 기록한다. 베어링 오일의 입구온도, 발전기 Cold Gas 온도 및 압력은 전부하 범위내에서 일정하게 유지되도록 한다.
② 각 베어링에서의 진동치를 Polar Graph에 그린다. 그림 3-44의 예에서 OA(40 ㎛∠330°)는 무부하시의 진동치이고 OB(116 ㎛∠309°)는 전부하에서 발전기 베어링의 진동치이다.
③ 무부하와 전부하시의 진동 벡터 끝을 연결한 열적 불평형 벡터 AB(40 ㎛∠300°)를 그래프상에서 구한다.
④ 발전기 로터의 Balance Sensitivity를 구하기 위하여 Fan Ring에 600 gr∠180°의 Static Pair Weight를 단다.
⑤ 발전기를 기동하여 무부하 상태에서의 진동치인 OC(104 ㎛∠720°)를 취한다. 이때 ①항에서 언급한 모든 변수들을 일정하게 유지 시킨다.
⑥ 벡터 AC(60 ㎛∠90°)는 Static Pair Weight에 의한 효과 벡터이다.
⑦ 그래프 상에서 0를 통과하며 벡터 AB와 크기가 같고 평행한 벡터 DE를 그린다. 이때 0는 벡터 DE의 중앙점이다.
⑧ 무부하시의 진동벡터 OA가 새로운 위치인 OD로 이동되도록 일면 발란싱 절차대로 시행한다. ∠DAC=44°이므로 180°에 달았던 Static Pair Weight를 반시계 방향으로 44° 이동한 224°(180° + 44°)로 옮기면 된다. 또한 달아야 할 무게는 벡터 AD가 38 ㎛이므로 600 gr
AD/AC = 600 gr
38 ㎛/60 ㎛ = 380 gr만 달면 된다.
⑨ Static Pair의 Trial Weight를 떼고 380 gr을 224°에 달면 무부하시의 진동은 OD가 된다. 이와 같이 발란싱은 원하는 위치로 이동시킬 수 있다. 물론 이 경우 전부하시의 진동은 OE(40 ㎛∠300°)가 될 것이다. 따라서 전부하에 걸쳐 진동은 허용치 이내에 있게된다.
8 다면 발란싱
Multi-Plane Balancing
앞에서 1면 발란싱의 기법을 이용하여 2면 발란싱 기법을 개발하였다. 마찬가지로 2면 발란싱 기법을 이용하면 다면 발란싱도 가능하다. 그러나 다면 발란싱의 경우도 2면 발란싱에서와 같이 Cross Effect를 고려해야 한다. 다면 발란싱의 최종목표는 기동시부터 전부하에 걸쳐 전체 로터 진동이 허용치 이내에 들도록 하는 것이다.
고압, 중압, 저압터빈 및 발전기로 구성된 기계를 예를 들어 설명한다. 저압터빈을 Static Balancing하여 진동이 원하는 값으로 감소되었다고 하자. 그러나 Cross Effect 영향으로 인접한 다른 로터의 진동진폭 및 위상각이 크게 변화하여 허용치 이상으로 증가하였다면 저압터빈에 달았던 교정 Weight와 무게를 조정하던가 진동이 상승한 로터를 다시 발란싱해야 한다.
따라서 각 로터마다 Static, Couple 또는 Single Balancing할 때마다 해당 로터에 미치는 Tagging Effect는 물론이고 인접 로터에 미치는 Cross Effect를 기록해 놓아야 이 값을 이용하여 발란싱 횟수를 최소한으로 할 수 있으며 전체 로터의 진동을 허용치 이내로 조정할 수 있다.
효과 벡터인 Tagging Effect와 Cross Effect를 구하기 위해서는 편의상 불평형 형태별로 일정한 무게와 각도(예를 들면 Static Unbalance인 경우는 전후 교정면에 200 gr∠0°의 Weight를 또 Couple Unbance인 경우는 전측 교정면에는 200 gr∠0°, 후측 교정면에는 200 gr∠180° Weight를 단다)를 선정하는 것이 좋다.
한편 Tagging Effect와 Cross Effect는 순수한 불평형에 의해서만 영향을 받지 않고 Alignment 상태나 Rubbing 등 외적인 진동원인에 의해서도 영향을 받으므로 그 값을 취할때마다 다소의 차이가 발생한다. 따라서 실제로 적용할 때는 현재의 상태에다 그 동안의 진동이력, Alignment 상태 등을 고려하여 Tagging 및 Cross Effect를 결정하여야 한다.