Free Vibration of Single Degree of Freedom Systems
다수의 기계와 구조물계는 1 자유도계로 단순화할 수 있다. 대부분의 실제 시스템에 있어서 질량은 분산되어 있으나 질량이 한 점에 집중된 것으로 보고 그 거동을 개략화할 수 있다.
2.1 비감쇠 병진계의 자유진동 (Free Vibration of an Undamped Translational System)
2.2 비감쇠 비틀림 시스템의 자유진동 (Free Vibration of Undamped Torsional System)
2.3 점성 감쇠율의 자유진동 (Free Vibration with Viscous Damping)
1-8-2-1 비감쇠 병진계의 자유진동
Free Vibration of an Undamped Translational System
2.1.1 뉴튼의 運動 第2法則을 利用한 運動方程式
(Equation of Motion Using Newton’s Second Law of Motion)
(1) 수평의 스프링-질량 시스템
그림 8-19(a)의 비감쇠 1 자유도계를 생각해 보자. 질량은 마찰이 없는 롤러에 지지되어 있고 수평방향으로 병진운동을 한다. 스프링의 당겨지지 않은 상태의 길이는![]() 이다. 질량을 정지상태로부터
이다. 질량을 정지상태로부터 ![]() 의 거리만큼의 위치에 놓으면 그림 8-19(c)에서와 같이 스프링력
의 거리만큼의 위치에 놓으면 그림 8-19(c)에서와 같이 스프링력 ![]() 를 야기 시킨다. 뉴튼의 제2법칙에 의하면
를 야기 시킨다. 뉴튼의 제2법칙에 의하면
질량×가속도 = 질량에 가해진 합성력 – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (40)
식 (40)을 m 에 적용하면 다음의 운동방정식을 세울 수 있다.
![]() 또는
또는 ![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (41)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (41)
![]() 에서 -의 의미는
에서 -의 의미는 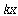 의 힘의 운동방향이
의 힘의 운동방향이 ![]() 의 힘의 운동방향과 정반대이기 때문에 등호를 성립시키기 위해서 -를 삽입하여야 하기 때문임. 또한 결과적으로 우변의 항을 좌변으로 옮긴
의 힘의 운동방향과 정반대이기 때문에 등호를 성립시키기 위해서 -를 삽입하여야 하기 때문임. 또한 결과적으로 우변의 항을 좌변으로 옮긴 ![]() 는 χ의 어느 위치에서나 합력은 “0”임을 의미한다. 여기서
는 χ의 어느 위치에서나 합력은 “0”임을 의미한다. 여기서 ![]() 는 질량의 가속도이다.
는 질량의 가속도이다.
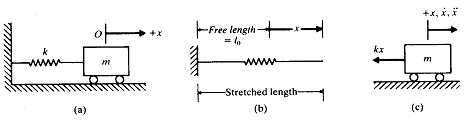
그림 8-19 수평의 스프링-질량시스템
(2) 수직의 스프링-질량 시스템
그림 8-20(a)에서 보는 바와 같은 스프링-질량시스템을 생각해보자. 질량 m 은 스프링의 아래쪽 끝에 매달려 있고 스프링의 다른 한쪽 끝은 벽에 고정되어 있다. 정지 상태에서 질량은 정적 평형위치라 불리는 위치에 매달려 있고 위쪽으로 향하는 스프링력이 아래쪽으로 향하는 중력과 정확하게 균형을 이루고 있다. 이 위치에서 스프링의 길이는![]() 이며 (
이며 (![]() 는 정적처짐) 질량 m 의 무게 W로 인한 신장량이다. 그림 8-20(a)에서 정적평형인 경우
는 정적처짐) 질량 m 의 무게 W로 인한 신장량이다. 그림 8-20(a)에서 정적평형인 경우
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (42)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (42)
여기서 g 는 중력가속도. 질량이 정적평형 위치에서![]() 만큼 움직이면 스프링력은 그림 8-20(c)에서와 같이
만큼 움직이면 스프링력은 그림 8-20(c)에서와 같이![]() 가 된다. 뉴튼의 운동 제2법칙을 질량 m 에 적용하면
가 된다. 뉴튼의 운동 제2법칙을 질량 m 에 적용하면
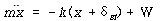
가 되며 -는 앞에서 설명한 바와 같은 의미이고 +W의 의미는 항상 지구 중심방향으로 W의 힘이 스프링에 작용하고 있음을 의미한다. 지구 중력에 의한 W는 항상 지구 중심방향으로 향하기 때문에 ![]() 와 W는 서로 상쇄된다.
와 W는 서로 상쇄된다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (43)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (43)
식 (41)과 식 (43)이 동일하다는 것을 알 수 있다. 즉 질량이 수직방향으로 움직일 때는 정적 평형 위치로부터![]() 를 측정하기 때문에 무게의 영향을 무시할 수 있다.
를 측정하기 때문에 무게의 영향을 무시할 수 있다.
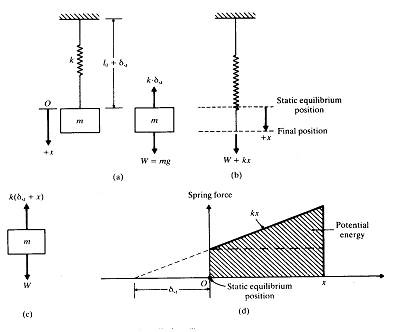
그림 8-20 수직방향의 스프링-질량시스템
2.1.2 에너지 保存의 原理를 利用한 運動方程式
(Equation of Motion Using the Principle of Conservation of Energy)
식 (41)은 또한 에너지보존의 원리를 이용하여 유도할 수 있다. 이 원리를 적용하기 위하여 우선 감쇠로 인한 에너지 소멸이 없어야 하며 그림 8-19(a)는 보존적이라고 한다. 진동중 시스템의 에너지는 일부가 운동에너지이고 나머지는 위치에너지이다. 운동에너지 T는 그 속도로 인하여 축적되고 위치에너지 U는 탄성변형으로 인하여 스프링에 축적된다. 에너지보존의 법칙에 따라
T + U = 일정 혹은 ![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (44)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (44)
운동 및 위치에너지는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (45)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (45)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (46)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (46)
식 (45) 및 식 (46)을 식 (44)에 대입하고 미분을 하게되면

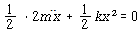
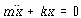
2.1.3 運動方程式의 解 (Solution of Motion Equation)
식 (41)의 해는 다음과 같이 가정함으로써 구할 수 있다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (47)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (47)
C 와 s는 결정되어야 할 상수이며
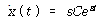
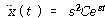
식 (41)에 대입하면
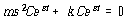
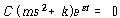
C 및 ![]() 는 0이 아니므로
는 0이 아니므로
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (48)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (48)
가 되고
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (49)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (49)
![]() 이며
이며
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (50)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (50)
식 (48)은 식 (41)의 미분방정식에 대응하는 보조 혹은 특성방정식이라 불린다.
식 (49)에 주어진 s의 두 값은 특성방정식의 근이며 문제의 고유치 혹은 특성치라고 알려져 있다.
s의 두 값은 식 (48)을 만족시키기 때문에 식 (41)의 일반해는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (51)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (51)
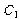 및
및 ![]() 는 상수이다.
는 상수이다.
오일러의 공식 ![]() 를 사용하여 식 (51)을 다시 쓰면
를 사용하여 식 (51)을 다시 쓰면
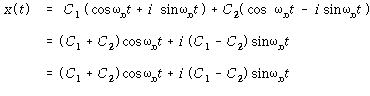 – – – – – – – – – – – – – (52)
– – – – – – – – – – – – – (52)
![]() 및
및 ![]() 는 새로운 상수이다. 상수
는 새로운 상수이다. 상수![]() 및
및![]() 혹은
혹은![]() 및
및![]() 는 시스템의 초기조건으로부터 결정되다. 만약, 변위
는 시스템의 초기조건으로부터 결정되다. 만약, 변위![]() 및 속도
및 속도 ![]() 가 t =0에서
가 t =0에서 ![]() 및
및 ![]() 로 주어지면 식 (52)로 부터
로 주어지면 식 (52)로 부터
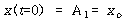
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (53)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (53)
그러므로, ![]() 및
및 ![]() 이 된다. 식 (53)의 초기조건에 좌우되는 식 (41)의 해는
이 된다. 식 (53)의 초기조건에 좌우되는 식 (41)의 해는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (54)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (54)
식 (52)는 다음과 같은 표현을 도입함으로써 다른 형태로 나타낼 수 있다.
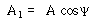
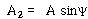
여기서 A 및 ψ는 새로운 상수이며 ![]() 및
및 ![]() 의 항으로 표시될 수 있다.
의 항으로 표시될 수 있다.
![]() = 진폭
= 진폭
![]() = 위상각
= 위상각
이를 식 (52)에 대입하면 그 해는
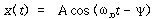
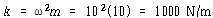
이 되어야 한다. 헬리컬 스프링의 강성은
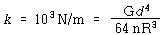
이 된다. 위의 식은 어떠한 설계를 하기 위한 출발점이 된다. 선택할 수 있는 것은 사용할 재료(즉, 여러 가지 값의 G), 재료의 직경 d, 코일의 반지름 R, 그리고 감은 수 n 등이다. G와 d 는 물론 얻을 수 있는 재료에 의해 제한되고 n은 정수가 되도록 제한되며, R은 기기의 크기에 따라 요구사항에 의한 제한을 받을 수 있다. 여기서 1 ㎝ 직경의 강철을 사용할 수 있다고 가정한다. 강철의 전단탄성계수는 약
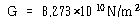
이 되므로 강성공식은
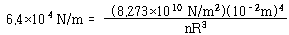
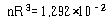
이 된다. 코일의 반지름을 10 ㎝로 선택하면 감은 수는
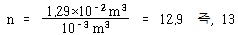
이 되어야 한다. 그러므로 1 ㎝ 직경의 강철을 반경 10 ㎝로 13회 감으면, 스프링은 원하는 강성을 갖고 10 ㎏의 질량은 약 10 rad/s로 진동할 것이다.
1-8-2-2 비감쇠 비틀림 시스템의 자유진동
Free Vibration of Undamped Torsional System
만약, 하나의 강체가 특정한 축에 관해서 진동할 때 결과적인 운동을 비틀림 진동이라 한다. 이 경우에 강체의 변위는 각좌표의 항으로 측정된다. 비틀림 진동 문제에 있어서 복귀 모멘트는 탄성체의 비틀림 혹은 힘이나 짝힘의 불평형 모멘트 때문일 것이다.
그림 8-21은 극관성 질량 모멘트 ![]() 인 디스크가 원형의 축 한쪽 끝에 설치되어 있고 다른 끝은 고정되어 있다. 축의 중심선에 대해 θ만큼 디스크를 각회전 시킨다 (θ는 축의 비틀림 각도를 나타낸다).
인 디스크가 원형의 축 한쪽 끝에 설치되어 있고 다른 끝은 고정되어 있다. 축의 중심선에 대해 θ만큼 디스크를 각회전 시킨다 (θ는 축의 비틀림 각도를 나타낸다).
원형축의 비틀림 이론으로부터
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (55)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (55)
![]() 는 비틀림θ를 일으키기 위한 토오크, G는 전단탄성계수, ℓ는 축의 길이, J는 축단면의 극관성모멘트이며
는 비틀림θ를 일으키기 위한 토오크, G는 전단탄성계수, ℓ는 축의 길이, J는 축단면의 극관성모멘트이며
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (56)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (56)
d 는 축의 직경을 의미한다. 만약, 디스크가 평형위치에서 θ만큼 움직였다면 축은 크기 ![]() 의 복귀 토오크를 제공한다. 그러므로, 축은 비틀림 스프링으로 거동하고 비틀림 스프링상수는
의 복귀 토오크를 제공한다. 그러므로, 축은 비틀림 스프링으로 거동하고 비틀림 스프링상수는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (57)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (57)
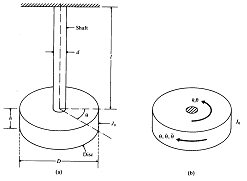
그림 8-21 디스크의 비틀림 진동
2.2.1 運動方程式 (Equation of Motion)
디스크의 2축에 관한 각운동 방정식은 뉴튼의 제2법칙 혹은 에너지 보존 원리를 사용하여 유도할 수 있다. 디스크의 자유물체 선도를 고려하여 뉴튼의 제2 운동법칙을 적용함으로써 운동방정식을 유도할 수 있다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (58)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (58)
식 (58)은 만약 극관성 질량모멘트![]() , 각 변위θ, 및 비틀림 스프링 상수
, 각 변위θ, 및 비틀림 스프링 상수![]() 가 질량 m , 변위
가 질량 m , 변위![]() 및 선형스프링 상수
및 선형스프링 상수![]() 로 각각 대치된다면 식 (41)과 동일함을 보여준다. 그러므로 비틀림 시스템의 고유각 주파수는
로 각각 대치된다면 식 (41)과 동일함을 보여준다. 그러므로 비틀림 시스템의 고유각 주파수는
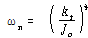 – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (59)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (59)
주기와 진동주파수는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (60)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (60)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (61)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (61)
이 비틀림 시스템에서 다음의 관점들에 주의하라.
① 디스크를 지지하고 있는 축의 단면이 원형이 아닌 경우는 적절한 비틀림 스프링계수를 이용하여야 한다.
② 디스크의 극관성 질량모멘트는
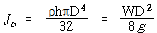
ρ는 질량밀도, h는 두께, D는 직경, 그리고 W는 디스크의 무게이다.
③ 그림 8-21의 비틀림 스프링-관성시스템은 비틀림 진자로서 언급된다. 비틀림 진자의 가장 중요한 적용중의 하나는 기계식 시계이며 라체트와 폴은 작은 비틀림 진자의 규칙적인 진동을 침의 움직임으로 변환하는 것이다.
2.2.2 解 (Solution)
식 (58)의 일반해는 식 (41)의 경우와 같이 구해진다.
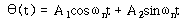 – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (62)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (62)
![]() ,
, ![]() 는 초기조건
는 초기조건
![]() ,
, ![]() – – – – – – – – – – – – – – – – – – – – – – – (63)
– – – – – – – – – – – – – – – – – – – – – – – (63)
로부터 구해지며
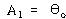
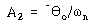 – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (64)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (64)
로 된다.
식 (62)도 또한 단순조화운동을 나타낸다.
1-8-2-3 점성 감쇠계의 자유진동
Free Vibration with Viscous Damping
2.3.1 運動方程式 (Equation of Motion)
점성감쇠력 F는 속도![]() 에 비례하며 다음과 같이 표현된다.
에 비례하며 다음과 같이 표현된다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (65)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (65)
c는 감쇠상수 혹은 점성감쇠계수이며 음의 부호는 감쇠력이 속도방향과 반대임을 의미한다. 점성댐퍼가 있는 1 자유도계가 그림 8-22에 제시되어 있다.
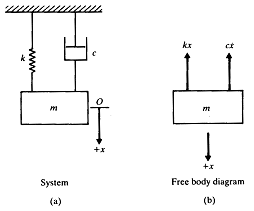
그림 8-22 점성댐퍼가 있는 1 자유도계
만약 질량 m 가 평형위치로부터 x 만큼 이동되었다면 뉴튼의 법칙에 따라 다음과 같이 운동방정식이 유도된다.
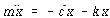
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (66)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (66)
2.3.2 解 (Solution)
식 (66)의 해를 구하기 위해 다음과 같은 형태의 해를 가정한다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (67)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (67)
여기서 c 와 s는 결정되지 않은 상수이다. 이 함수를 식 (67)에 대입하면 다음과 같은 특성방정식을 구하게 된다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (68)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (68)
그 근은
![]() – – – – – – – – – – – – – – – – – – – (69)
– – – – – – – – – – – – – – – – – – – (69)
이 근은 2개의 해를 제시하며
![]() 및
및 ![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (70)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (70)
식 (66)의 일반해는 두 해의 선형조합으로 주어진다.
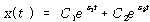
임계 감쇠상수와 감쇠비 : 임계 감쇠 ![]() 는 식 (69)의 근호내에 있는 감쇠상수 c가 0이 되는 것으로 정의한다.
는 식 (69)의 근호내에 있는 감쇠상수 c가 0이 되는 것으로 정의한다.
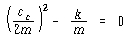
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (71)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (71)
어떠한 감쇠 시스템에서 감쇠비 ζ는 임계 감쇠상수에 대한 감쇠상수의 비로서 나타낸다.
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (72)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (72)
식 (71)과 식 (72)으로부터
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (73)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (73)
즉
![]() (74)
(74)
![]() – – – – – – – – – – – – – – – – – – – – – – (75)
– – – – – – – – – – – – – – – – – – – – – – (75)
근![]() 과
과 ![]() 의 특성 및 식 (75)의 거동은 감쇠의 크기에 좌우된다. ζ=0의 경우는 앞 절에서 설명되었기 때문에 ζ≠0로 가정하고 다음의 3가지 경우에 대해 생각해 보기로 한다.
의 특성 및 식 (75)의 거동은 감쇠의 크기에 좌우된다. ζ=0의 경우는 앞 절에서 설명되었기 때문에 ζ≠0로 가정하고 다음의 3가지 경우에 대해 생각해 보기로 한다.
경우 1 부족감쇠시스템 (ζ<1 혹은 ![]() 혹은
혹은 ![]() )
)
이와 같은 경우 ![]() 은 음이고 근
은 음이고 근 ![]() 는 다음과 같이 표현된다.
는 다음과 같이 표현된다.
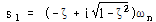
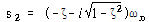
식 (75)는 다음과 같이 다른 형태로 표현할 수 있다.
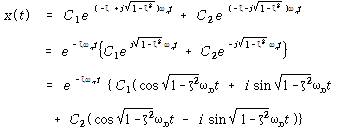
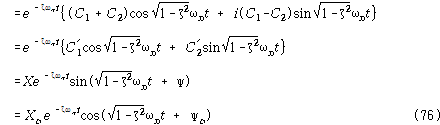
여기서![]() , (χ,ψ) 및
, (χ,ψ) 및![]() 는 임의상수이며 초기조건으로부터 결정된다.
는 임의상수이며 초기조건으로부터 결정된다.
초기조건 ![]() 와
와 ![]() 일 때,
일 때, ![]() 및
및 ![]() 는 다음과 같이 구해진다.
는 다음과 같이 구해진다.
![]() 에 t =0을 대입하면
에 t =0을 대입하면
![]() 가 되고, 위 식을 미분하면
가 되고, 위 식을 미분하면
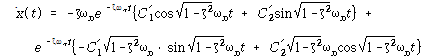
가 되고 t =0을 대입하면,
![]() 가 된다.
가 된다.
![]() 를 위 식에 대입하면
를 위 식에 대입하면
![]() 가 되고 결과적으로
가 되고 결과적으로
∴ ![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (77)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (77)
가 된다.
![]() 를 원식에 대입하면
를 원식에 대입하면
![]() – – – – – – – – – – – – (78)
– – – – – – – – – – – – (78)
상수 (Χ, ψ) 및 (![]() )는
)는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (79)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (79)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (80)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (80)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (81)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (81)
식 (78)에 의해 표시되는 운동은 각 주파수 ![]() 의 조화운동이지만
의 조화운동이지만 ![]() 로 인하여 진폭은 시간의 경과와 더불어 지수적으로 감소한다 (그림 8-23).
로 인하여 진폭은 시간의 경과와 더불어 지수적으로 감소한다 (그림 8-23).
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (82)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (82)
![]() 는 감쇠진동의 고유 주파수라고 하며 항상 비감쇠 고유진동수
는 감쇠진동의 고유 주파수라고 하며 항상 비감쇠 고유진동수![]() 보다는 작다.
보다는 작다.

그림 8-23 부족감쇠의 해
감쇠량의 증가에 따른 감쇠 진동 주파수의 감소가 그림 8-24에 나타나 있다.



부족감쇠의 경우가 기계진동의 연구에 있어 가장 중요하며 그 이유는 유일하게 진동운동을 하기 때문이다.

그림 8-24 감쇠의 크기에 따른 ωd의 변화
경우2 : 임계 감쇠 시스템 (ζ=1 혹은 ![]() 혹은
혹은 ![]() )
)
식 (69)에서![]() 이므로 2개의 근
이므로 2개의 근![]() 는 같고
는 같고
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (83)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (83)
이 된다.
중근이기 때문에 식 (68)의 해는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (84)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (84)
초기조건![]() 와
와 ![]() 를 적용하여
를 적용하여



![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (85)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (85)
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (86)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (86)
식 (86)에 의해 표현되는 운동은 비주기적이다.
t = ∞이면 ![]() =”0″으로 되기 때문에 운동은 결국 그림 8-25에서 나타낸 바와 같이 진폭이 0으로 되어 사라진다.
=”0″으로 되기 때문에 운동은 결국 그림 8-25에서 나타낸 바와 같이 진폭이 0으로 되어 사라진다.

그림 8-25 감쇠의 형태에 따른 운동의 비교
경우3 : 과감쇠 진동시스템 (ζ>1 혹은 ![]() 혹은
혹은![]() )
)
![]() >0 때문에
>0 때문에 ![]() 및
및 ![]() 는 실수이며
는 실수이며



![]() – – – – – – – – – – – – – – – – – – – – – – – (87)
– – – – – – – – – – – – – – – – – – – – – – – (87)
초기조건 ![]() 와
와 ![]() 로부터
로부터 ![]() 과
과 ![]() 가 구해진다. 즉,
가 구해진다. 즉,
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (88)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (88)

![]() – – – – – – – – – – – – – – – – – – – – – (89)
– – – – – – – – – – – – – – – – – – – – – (89)


![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (90)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (90)



![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (91)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (91)
식 (87)로부터 이 시스템에 가해진 초기조건에는 관계없이 주기적인 운동을 함을 알 수 있다. 근 ![]() ,
, ![]() 는 음이기 때문에 운동은 시간의 경과에 따라 지수적으로 감소하고 사라진다 (그림 8-25).
는 음이기 때문에 운동은 시간의 경과에 따라 지수적으로 감소하고 사라진다 (그림 8-25).
2.3.3 代數 減衰率 (Logarithmic Decrement)
대수 감쇠율은 자유감쇠진동의 진폭이 감소하는 비를 나타낸다. 어떤 2개의 연속되는 진폭의 자연대수비로서 정의된다. ![]() 과
과 ![]() 를 2개의 연속되는 진폭에 대응하는 시각을 나타낸다고 하면 각각의 시각에서의 부족감쇠시스템의 진폭은 다음과 같이 된다.
를 2개의 연속되는 진폭에 대응하는 시각을 나타낸다고 하면 각각의 시각에서의 부족감쇠시스템의 진폭은 다음과 같이 된다.
![]() 은 임의의 시간 에서의 진동진폭이고
은 임의의 시간 에서의 진동진폭이고 ![]() 는
는 ![]() 에서의 진동진폭이므로
에서의 진동진폭이므로
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (92)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (92)
가 된다.
여기서 ![]() (
(![]() : 감쇠진동의 주기)이다.
: 감쇠진동의 주기)이다.
![]() 와 같게 되므로 식 (92)는
와 같게 되므로 식 (92)는
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (93)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (93)
대수 감쇠율 δ는 식 (93)으로부터

![]() – – – – – – – – – – – – – – – – – (94)
– – – – – – – – – – – – – – – – – (94)
감쇠가 작을 경우 식 (94)는 간략하게 다음과 같이 나타낼 수 있다.
δ = 2πζ (만약 ζ << 1인 경우) – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (95)
그림 8-26은 ζ에 따른 대수 감쇠율 δ의 변화를 보여준다. ζ= 0.3까지의 δ값은 식 (94)과 식 (95)에서 거의 동일한 값을 나타낸다.
대수감쇠율은 무차원이고 실제적으로 무차원 감쇠비 ζ의 다른 형태이다. 일단 δ가 기지의 값이라면 식 (94)로부터 ζ를 구할 수 있다.




∴![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (96)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (96)
만약 식 (94) 대신에 식 (95)를 사용한다면
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (97)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (97)

그림 8-26 감쇠값에 따른 대수감쇠율의 변화
주어진 진동 시스템에서 감쇠값이 알려져 있지 않으면 실험적으로 두 개의 연속되는 변위 ![]() 과
과 ![]() 를 측정함으로서 구할 수 있다.
를 측정함으로서 구할 수 있다. ![]() 과
과 ![]() 의 자연대수비를 취함으로써 δ를 얻을 수 있다.
의 자연대수비를 취함으로써 δ를 얻을 수 있다.
식 (96)을 사용함으로써 감쇠비 ζ를 계산할 수 있다. 실제적으로는 감쇠비 ζ는 수 개의 사이클에 의해 분리된 처음과 끝의 두 변위를 측정함으로써도 구할 수 있다.
만약 ![]() 과
과 ![]() 이 시간
이 시간 ![]() 과
과 ![]() 에 상응하는 진폭이라면
에 상응하는 진폭이라면
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (98)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – (98)
어떤 두개의 연속된 변위는 한 사이클에 의해 분리되기 때문에
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (99)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (99)
식 (98)은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (100)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (100)
식 (100)과 식 (94)로부터


![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (101)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (101)

그림 8-27
[해]![]() ,
, ![]() 이 되며 대수감쇠율
이 되며 대수감쇠율
![]() – – – – – – – – – – – – – – – – – – – – – (102)
– – – – – – – – – – – – – – – – – – – – – (102)
식 (102)로부터 ζ=0.4037, 진동주기는 1 sec이므로


임계감쇠상수는
![]() = 2(500) (6.8677) = 6887.7 N•s/m
= 2(500) (6.8677) = 6887.7 N•s/m
감쇠상수는
![]() = (0.4037)(6867.7) = 2772.4905 N•s/m
= (0.4037)(6867.7) = 2772.4905 N•s/m
강성은
![]() = (500)(6.8677)2 = 23582.652 N/m
= (500)(6.8677)2 = 23582.652 N/m
질량의 변위는 시각 ![]() 에서 최대값을 갖으며
에서 최대값을 갖으며



최대점을 통과하는 그림 8-23의 점선의 χ값은
![]() – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (103)
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – (103)
χ = 250 ㎜이므로 식 (103)은


질량의 속도는 변위를 미분함으로써 얻을 수 있으며

![]() – – – – – – – – – – – – – – – – – – – – (104)
– – – – – – – – – – – – – – – – – – – – (104)
t = 0 일 때 식 (104)은

